2020版八年级数学下册2.6.2菱形的判定课件(31张ppt)(新版)湘教版
文档属性
| 名称 | 2020版八年级数学下册2.6.2菱形的判定课件(31张ppt)(新版)湘教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
2.6.2 菱形的判定
【知识再现】
菱形有哪些特殊性质?
边:四条边都_________;?
角:对角线平分一组_________;?
相等
对角
对角线:对角线互相_________且平分,对角线的
交点是它的对称中心,___________所在的直线是
它的对称轴.?
垂直
对角线
【新知预习】阅读教材P68-P70,解决以下问题:
目标一:会用菱形的定义判定一个四边形是否是菱形,并会用该种方法进行有关的证明.
菱形的定义:
有一组_____________的平行四边形叫作菱形.?
用符号语言可以表示为:∵四边形ABCD是
_________四边形,?
AB=BC,∴四边形ABCD是菱形.
邻边相等
平行
目标二:探究并掌握菱形的判定方法
1.(1)用尺规画出菱形ABCD
(2)你发现四边形ABCD四边的关系是_________;?
你发现的规律:_____________________________.?
相等
四条边相等的四边形是菱形
2.(1)由“在一长一短的木条中点处固定一个小钉”
可知:_______=_______,_______=________
∴四边形ABCD是_______形?
AO
CO
BO
DO ?
菱
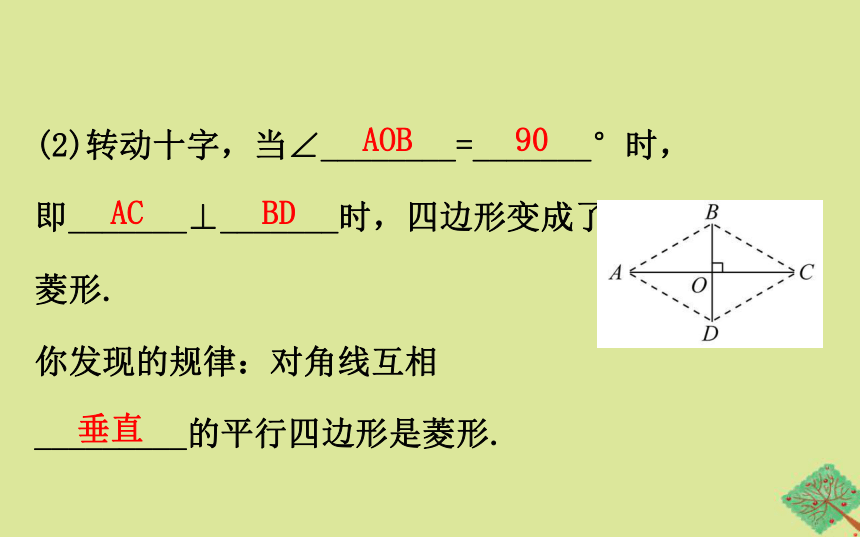
(2)转动十字,当∠________=_______°时,?
即_______⊥_______时,四边形变成了
菱形.?
你发现的规律:对角线互相
_________的平行四边形是菱形.?
AOB
90
AC
BD
垂直
【基础小练】
请自我检测一下预习的效果吧!
1.从下列条件中选择一个条件添加后,还不能判定
平行四边形ABCD是菱形,则这个条件是 ( )
A.AC⊥BD B.AD=CD
C.AB=BC D.AC=BD
D
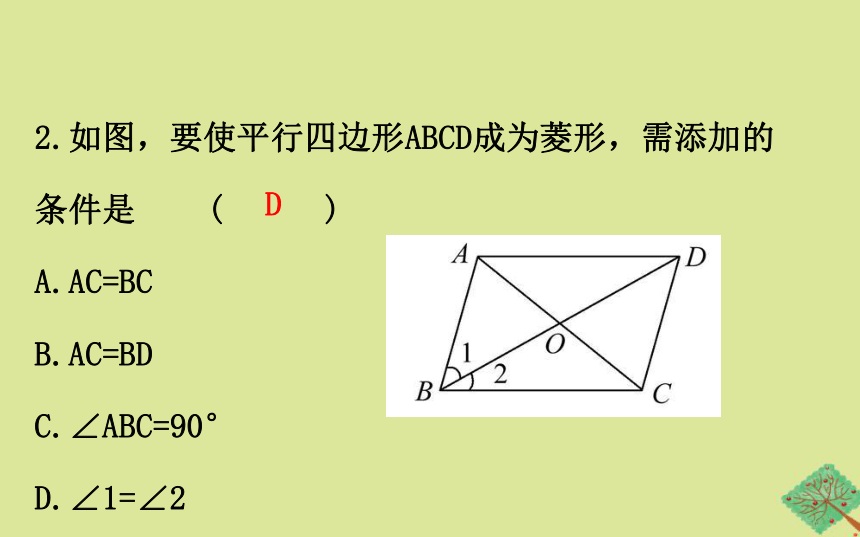
2.如图,要使平行四边形ABCD成为菱形,需添加的
条件是 ( )
A.AC=BC
B.AC=BD
C.∠ABC=90°
D.∠1=∠2
D
知识点 菱形的判定及应用(P68例2拓展)
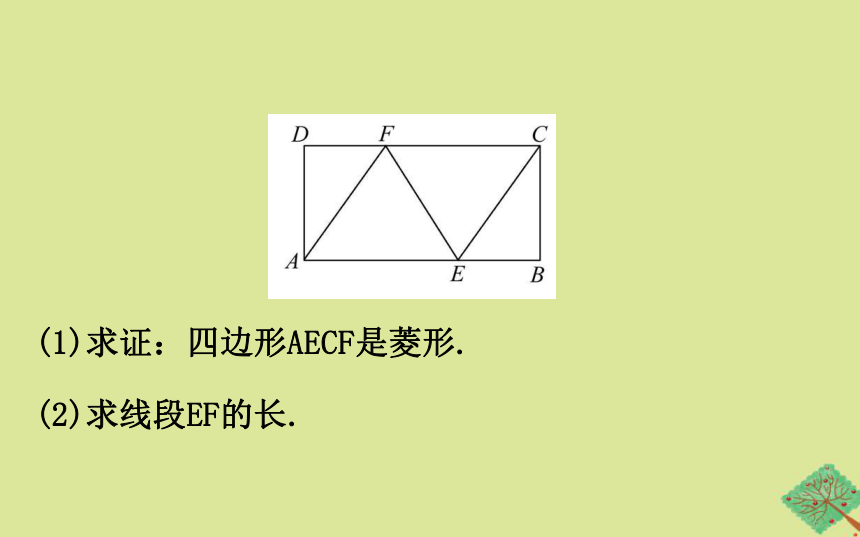
【典例】(2019·宿迁中考)如图,矩形ABCD中,AB=4,BC=2,点E,F分别在AB,CD上,且BE=DF= . .
(1)求证:四边形AECF是菱形.
(2)求线段EF的长.
【自主解答】略
【学霸提醒】菱形的常用判定方法
已有条件 需要条件
平行四边形 邻边相等
对角线互相垂直
每条对角线平分一组对角
一般四边形 四条边都相等
对角线互相垂直平分
对角线互相平分,且每条对角线平分一组对角
【题组训练】
1.如图,将△ABC沿BC方向平移得到△DCE,连接AD,
下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60°
A
★2.(2019·滕州模拟)如图,在∠MON的两边上分别截
取OA,OB,使OA=OB;分别以点A,B为圆心,OA长为半
径作弧,两弧交于点C;连接AC,BC,AB,OC.若AB=
2 cm,四边形OACB的面积为4 cm2.则OC的长为 ( )
C
A.2 cm B.3 cm
C.4 cm D.5 cm
★3.一个平行四边形的一条边长为3,两条对角线的
长分别为4和2 ,则它的面积为______.?
★★4.(2019 ·宁德市期末)利用所给的图形证明:一个顶点到它所对的两边距离相等的平行四边形是菱形.(写出已知、求证并加以证明) .
已知:
求证:
证明:
解:已知:在?ABCD中,DE⊥AB,DF⊥BC,DE=DF,
求证:?ABCD是菱形.
证明:∵四边形ABCD是平行四边形,∴∠A=∠C,
∵DE⊥AB,DF⊥BC,∴∠DEA=∠DFC=90°,
又∵DE=DF,∴△DAE≌△DCF(AAS),
∴DA=DC,∴?ABCD是菱形.
【火眼金睛】
如图,在?ABCD中,∠BAD的平分线AE与BC相交于点E,∠ABC的平分线BF与AD相交于点F,AE与BF相交于点O,求证:四边形ABEF是菱形.
【正解】∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠2=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠1=∠2,∴∠1=∠BEA,
∴BA=BE,同理可得AB=AF,∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,∴四边形ABEF是菱形.
【一题多变】
如图,∠ACB=90°,点E是AB边的中点.点F恰是点E关于AC所在直线的对称点. .
(1)证明:四边形CFAE为菱形.
(2)连接EF交AC于点O.若BC=2 ,求线段OF的长.
解:(1)∵∠ACB=90°,点E是AB边的中点
∴CE= AB=EA,
∵点F恰是点E关于AC所在直线的对称点,
∴AE=AF,CE=CF,
∴CE=EA=AF=CF,∴四边形CFAE是菱形.
(2)略
【母题变式】
【变式一】已知,如图,AD是△ABC的角平分线,DE∥AC,AF=ED.
求证:四边形AEDF是菱形.
证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,∵DE∥AC,ED=AF,
∴四边形AEDF是平行四边形,
∴∠EAD=∠ADF,∴∠FAD=∠FDA,
∴AF=DF,∴四边形AEDF是菱形.
【变式二】如图:在△ABC中,∠BAC=90°,AD⊥BC于点D,CE平分∠ACB,交AD于点G,交AB于点E,EF⊥BC于点F.
求证:四边形AEFG是菱形.
.
略
2.6.2 菱形的判定
【知识再现】
菱形有哪些特殊性质?
边:四条边都_________;?
角:对角线平分一组_________;?
相等
对角
对角线:对角线互相_________且平分,对角线的
交点是它的对称中心,___________所在的直线是
它的对称轴.?
垂直
对角线
【新知预习】阅读教材P68-P70,解决以下问题:
目标一:会用菱形的定义判定一个四边形是否是菱形,并会用该种方法进行有关的证明.
菱形的定义:
有一组_____________的平行四边形叫作菱形.?
用符号语言可以表示为:∵四边形ABCD是
_________四边形,?
AB=BC,∴四边形ABCD是菱形.
邻边相等
平行
目标二:探究并掌握菱形的判定方法
1.(1)用尺规画出菱形ABCD
(2)你发现四边形ABCD四边的关系是_________;?
你发现的规律:_____________________________.?
相等
四条边相等的四边形是菱形
2.(1)由“在一长一短的木条中点处固定一个小钉”
可知:_______=_______,_______=________
∴四边形ABCD是_______形?
AO
CO
BO
DO ?
菱
(2)转动十字,当∠________=_______°时,?
即_______⊥_______时,四边形变成了
菱形.?
你发现的规律:对角线互相
_________的平行四边形是菱形.?
AOB
90
AC
BD
垂直
【基础小练】
请自我检测一下预习的效果吧!
1.从下列条件中选择一个条件添加后,还不能判定
平行四边形ABCD是菱形,则这个条件是 ( )
A.AC⊥BD B.AD=CD
C.AB=BC D.AC=BD
D
2.如图,要使平行四边形ABCD成为菱形,需添加的
条件是 ( )
A.AC=BC
B.AC=BD
C.∠ABC=90°
D.∠1=∠2
D
知识点 菱形的判定及应用(P68例2拓展)
【典例】(2019·宿迁中考)如图,矩形ABCD中,AB=4,BC=2,点E,F分别在AB,CD上,且BE=DF= . .
(1)求证:四边形AECF是菱形.
(2)求线段EF的长.
【自主解答】略
【学霸提醒】菱形的常用判定方法
已有条件 需要条件
平行四边形 邻边相等
对角线互相垂直
每条对角线平分一组对角
一般四边形 四条边都相等
对角线互相垂直平分
对角线互相平分,且每条对角线平分一组对角
【题组训练】
1.如图,将△ABC沿BC方向平移得到△DCE,连接AD,
下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60°
A
★2.(2019·滕州模拟)如图,在∠MON的两边上分别截
取OA,OB,使OA=OB;分别以点A,B为圆心,OA长为半
径作弧,两弧交于点C;连接AC,BC,AB,OC.若AB=
2 cm,四边形OACB的面积为4 cm2.则OC的长为 ( )
C
A.2 cm B.3 cm
C.4 cm D.5 cm
★3.一个平行四边形的一条边长为3,两条对角线的
长分别为4和2 ,则它的面积为______.?
★★4.(2019 ·宁德市期末)利用所给的图形证明:一个顶点到它所对的两边距离相等的平行四边形是菱形.(写出已知、求证并加以证明) .
已知:
求证:
证明:
解:已知:在?ABCD中,DE⊥AB,DF⊥BC,DE=DF,
求证:?ABCD是菱形.
证明:∵四边形ABCD是平行四边形,∴∠A=∠C,
∵DE⊥AB,DF⊥BC,∴∠DEA=∠DFC=90°,
又∵DE=DF,∴△DAE≌△DCF(AAS),
∴DA=DC,∴?ABCD是菱形.
【火眼金睛】
如图,在?ABCD中,∠BAD的平分线AE与BC相交于点E,∠ABC的平分线BF与AD相交于点F,AE与BF相交于点O,求证:四边形ABEF是菱形.
【正解】∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠2=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠1=∠2,∴∠1=∠BEA,
∴BA=BE,同理可得AB=AF,∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,∴四边形ABEF是菱形.
【一题多变】
如图,∠ACB=90°,点E是AB边的中点.点F恰是点E关于AC所在直线的对称点. .
(1)证明:四边形CFAE为菱形.
(2)连接EF交AC于点O.若BC=2 ,求线段OF的长.
解:(1)∵∠ACB=90°,点E是AB边的中点
∴CE= AB=EA,
∵点F恰是点E关于AC所在直线的对称点,
∴AE=AF,CE=CF,
∴CE=EA=AF=CF,∴四边形CFAE是菱形.
(2)略
【母题变式】
【变式一】已知,如图,AD是△ABC的角平分线,DE∥AC,AF=ED.
求证:四边形AEDF是菱形.
证明:∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,∵DE∥AC,ED=AF,
∴四边形AEDF是平行四边形,
∴∠EAD=∠ADF,∴∠FAD=∠FDA,
∴AF=DF,∴四边形AEDF是菱形.
【变式二】如图:在△ABC中,∠BAC=90°,AD⊥BC于点D,CE平分∠ACB,交AD于点G,交AB于点E,EF⊥BC于点F.
求证:四边形AEFG是菱形.
.
略
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
