2020版八年级数学下册2.7正方形课件(48张ppt)(新版)湘教版
文档属性
| 名称 | 2020版八年级数学下册2.7正方形课件(48张ppt)(新版)湘教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 16:22:52 | ||
图片预览











文档简介
(共48张PPT)
2.7 正 方 形
【知识再现】
1.菱形的四条边都_________,矩形的四个角都为
_________.?
2.菱形的对角线互相_________,矩形的对角线
_________.?
相等
直角
垂直
相等
【新知预习】阅读教材P72-P74,归纳结论:
1.定义:有一组邻边_________且有一个角是
_________的平行四边形叫作正方形.(正方形既是矩形又是菱形).?
相等
直角
2.性质:①正方形的四条边_________,四个角都是
_________.②正方形的两条对角线相等,并且互相
_____________.每条对角线_________一组对角.
③正方形既是轴对称图形,又是中心对称图形.?
相等
直角
垂直平分
平分
3.判定:①矩形+一组邻边_________=正方形;
②矩形+对角线互相_________=正方形;③菱形+
一个角为_________=正方形;④菱形+对角线
_________=正方形.
相等
垂直
直角
相等
【基础小练】
请自我检测一下预习的效果吧!
1.(2019 ·成都简阳期末)正方形具有而菱形不一定
具有的特征有 ( )
C
A.对角线互相垂直平分
B.内角和为360°
C.对角线相等
D.对角线平分内角
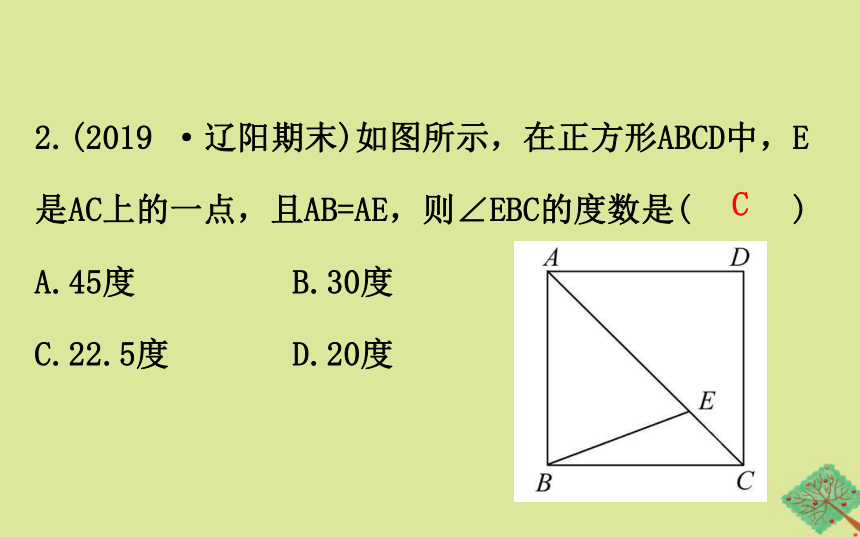
2.(2019 ·辽阳期末)如图所示,在正方形ABCD中,E
是AC上的一点,且AB=AE,则∠EBC的度数是( )
A.45度 B.30度
C.22.5度 D.20度
C
知识点一 正方形的性质(P73例1拓展)
【典例1】(2019·长沙中考)如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF.
(2)若AB=4,DE=1,求AG的长.
【自主解答】(1)∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,∴AE=DF,
在△BAE和△ADF中,
∴△BAE≌△ADF(SAS),∴BE=AF.
(2)略
【学霸提醒】正方形的“边、角、对角线”
1.边:四条边都相等且每组对边平行.
2.角:四个角都是直角.
3.对角线:两条对角线相等且互相垂直平分,把正方
形分成四个全等的等腰直角三角形;每条对角线平分
一组对角,把正方形分成两个全等的等腰直角三角形.
【题组训练】
1.矩形、菱形、正方形都具有的性质是 ( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
C
★2.如图,正方形ABCD的四个顶点A,B,C,D正好
分别在四条平行线l1,l2,l3,l4上.若从上到下每
两条平行线间的距离都是2 cm,则正方形ABCD的
面积为 ( )
.
C
A.4 cm2 B.5 cm2
C.20 cm2 D.30 cm2
★3.(2019·聊城阳谷一模)如图,将边长为 的正
方形绕点B逆时针旋转30°,那么图中点M的坐标为
.( )
A.( ,1) B.(1, )
C.( , ) D.( , )
B
★★4.如图,正方形ABCD和正方形CEFG中,
点D在CG上,BC=1,CE=3,H是AF的中点,
那么CH的长是 ( )
A
知识点二 正方形的判定(P73例2拓展)
【典例2】已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
【思路点拨】先由BF∥CE,CF∥BE得出四边形BECF是平行四边形,又因为∠BEC=90°得出四边形BECF是矩形,又BE=CE得出邻边相等的矩形是正方形.
【自主解答】∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形,
又∵在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ECB=45°,
∴∠BEC=90°,BE=CE,
∴四边形BECF是正方形.
【学霸提醒】 判定正方形的一般思路
【题组训练】
1.(2019 ·白银靖远期末)在四边形ABCD中,O是
对角线AC,BD的交点,能判定这个四边形为正方形
的是 ( )
D
A.AD∥BC,∠B=∠D
B.AC=BD,AB=CD,AD=BC
C.OA=OC,OB=OD,AB=BC
D.OA=OB=OC=OD,AC⊥BD
★2.如图,在△ABC中,O是AC上一动点,过点O作直线
MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角
平分线于点F,若点O运动到AC的中点,且∠ACB=
______时,四边形AECF是正方形. .
( )?
D
A.30° B.45° C.60° D.90°
★3.(2019·云南模拟)如图,平行四边形ABCD的对角
线互相垂直,要使ABCD成为正方形,还需添加的一个
条件是__________________________________(只需
添加一个即可)?
∠ABC=90°或AC=BD(答案不唯一)
★★4.如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD, .
(1)求证:AO=EO.
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
解:(1)∵AD∥BC,∴∠CBD=∠ADB,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AB=AD,又∵AE⊥BD,∴BO=DO,又∵∠AOD=∠EOB,∴△AOD≌△EOB,∴AO=EO.
(2)当△ABC满足∠ABC=90°时,四边形ABED是正方形.理由:∵△AOD≌△EOB,∴AD=BE,
又∵AD∥BE,AE⊥BD,∴四边形ABED是菱形,∴当∠ABC=90°时,菱形ABED是正方形,即当△ABC满足∠ABC=90°时,四边形ABED是正方形.
【火眼金睛】
如图,点E,F,M,N分别是正方形ABCD四条边上的点,若AE=BF=CM=DN,则四边形EFMN是什么图形?证明你的结论.
【正解】四边形EFMN是正方形,理由:
∵AE=BF=CM=DN,
∴AN=DM=CF=BE,
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DNM≌△CMF≌△BFE.
∴EF=EN=NM=MF,∠ENA=∠DMN.
∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°,∴∠ENM=90°.
∴四边形EFMN是正方形.
【一题多变】
如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF..
(1)求证:AE=CF.
(2)连接DB交EF于点O,延长OB至点G,使OG=OD,连接EG,FG,判断四边形DEGF是怎样的四边形,并说明理由.
解:(1)∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°,
在△DAE和△DCF中,
∴△DAE≌△DCF,∴AE=CF.
(2)四边形DEGF是菱形,∵△DAE≌△DCF,
∴DE=DF,∵AE=CF,∴BE=BF,
∴DG是EF的垂直平分线,∴GE=GF,
∵OG=OD,DG⊥EF,∴ED=EG,
∴DE=EG=GF=FD,∴四边形DEGF是菱形.
【母题变式】
【变式一】(变换条件与问法)已知:在菱形ABCD中,E,F在BD上,∠ABC=45°,BE=DF=AE,求证:四边形AECF是正方形.
证明:如图,连接AC交BD于点O,
∵四边形ABCD是菱形,∴AO=CO,BO=DO,AC⊥BD,AB=AD,∠ABE= ∠ABC=22.5°.
∵BE=DF,∴OE=OF,
又∵AO=CO,∴四边形AECF是平行四边形,
∵AC⊥BD,∴四边形AECF是菱形,∴AE=AF,
∵AE=BE,∴∠ABE=∠BAE=22.5°,
∴∠AEF=∠ABE+∠BAE=45°,
∵AE=AF,∴∠AEF=∠AFE=45°,
∴∠EAF=90°,∴菱形AECF是正方形.
【变式二】(变换条件与问法)如图,在边长为2的正方形ABCD中,AE⊥DH于E,BF⊥AE于F,CG⊥BF于G,DH⊥CG于H,且∠ABF=∠BCG=∠CDH=∠DAE=30°.
(1)求证:四边形EFGH为正方形.
(2)求正方形EFGH的面积.
解:(1)∵AE⊥DH,DH⊥CG,∴AE∥CG,
同理:BF∥DH,∴四边形EFGH是平行四边形,
∵AE⊥DH,∴∠FEH=90°,
∴平行四边形EFGH是矩形,
∵四边形ABCD是正方形,∴AD=AB,
在△ABF和△DAE中
∴△ABF≌△DAE,∴AF=DE,BF=AE,
∴FG=FE,∴矩形EFGH是正方形.
(2)在Rt△ABF中,∠ABF=30°,AB=2,
∴AF=1,BF= ,
同理:AE= ,∴EF=AE-AF= -1,
∴S正方形EFGH=EF2=( -1)2=4-2 .
2.7 正 方 形
【知识再现】
1.菱形的四条边都_________,矩形的四个角都为
_________.?
2.菱形的对角线互相_________,矩形的对角线
_________.?
相等
直角
垂直
相等
【新知预习】阅读教材P72-P74,归纳结论:
1.定义:有一组邻边_________且有一个角是
_________的平行四边形叫作正方形.(正方形既是矩形又是菱形).?
相等
直角
2.性质:①正方形的四条边_________,四个角都是
_________.②正方形的两条对角线相等,并且互相
_____________.每条对角线_________一组对角.
③正方形既是轴对称图形,又是中心对称图形.?
相等
直角
垂直平分
平分
3.判定:①矩形+一组邻边_________=正方形;
②矩形+对角线互相_________=正方形;③菱形+
一个角为_________=正方形;④菱形+对角线
_________=正方形.
相等
垂直
直角
相等
【基础小练】
请自我检测一下预习的效果吧!
1.(2019 ·成都简阳期末)正方形具有而菱形不一定
具有的特征有 ( )
C
A.对角线互相垂直平分
B.内角和为360°
C.对角线相等
D.对角线平分内角
2.(2019 ·辽阳期末)如图所示,在正方形ABCD中,E
是AC上的一点,且AB=AE,则∠EBC的度数是( )
A.45度 B.30度
C.22.5度 D.20度
C
知识点一 正方形的性质(P73例1拓展)
【典例1】(2019·长沙中考)如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF.
(2)若AB=4,DE=1,求AG的长.
【自主解答】(1)∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD,
∵DE=CF,∴AE=DF,
在△BAE和△ADF中,
∴△BAE≌△ADF(SAS),∴BE=AF.
(2)略
【学霸提醒】正方形的“边、角、对角线”
1.边:四条边都相等且每组对边平行.
2.角:四个角都是直角.
3.对角线:两条对角线相等且互相垂直平分,把正方
形分成四个全等的等腰直角三角形;每条对角线平分
一组对角,把正方形分成两个全等的等腰直角三角形.
【题组训练】
1.矩形、菱形、正方形都具有的性质是 ( )
A.对角线相等 B.对角线平分一组对角
C.对角线互相平分 D.对角线互相垂直
C
★2.如图,正方形ABCD的四个顶点A,B,C,D正好
分别在四条平行线l1,l2,l3,l4上.若从上到下每
两条平行线间的距离都是2 cm,则正方形ABCD的
面积为 ( )
.
C
A.4 cm2 B.5 cm2
C.20 cm2 D.30 cm2
★3.(2019·聊城阳谷一模)如图,将边长为 的正
方形绕点B逆时针旋转30°,那么图中点M的坐标为
.( )
A.( ,1) B.(1, )
C.( , ) D.( , )
B
★★4.如图,正方形ABCD和正方形CEFG中,
点D在CG上,BC=1,CE=3,H是AF的中点,
那么CH的长是 ( )
A
知识点二 正方形的判定(P73例2拓展)
【典例2】已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
【思路点拨】先由BF∥CE,CF∥BE得出四边形BECF是平行四边形,又因为∠BEC=90°得出四边形BECF是矩形,又BE=CE得出邻边相等的矩形是正方形.
【自主解答】∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形,
又∵在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ECB=45°,
∴∠BEC=90°,BE=CE,
∴四边形BECF是正方形.
【学霸提醒】 判定正方形的一般思路
【题组训练】
1.(2019 ·白银靖远期末)在四边形ABCD中,O是
对角线AC,BD的交点,能判定这个四边形为正方形
的是 ( )
D
A.AD∥BC,∠B=∠D
B.AC=BD,AB=CD,AD=BC
C.OA=OC,OB=OD,AB=BC
D.OA=OB=OC=OD,AC⊥BD
★2.如图,在△ABC中,O是AC上一动点,过点O作直线
MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角
平分线于点F,若点O运动到AC的中点,且∠ACB=
______时,四边形AECF是正方形. .
( )?
D
A.30° B.45° C.60° D.90°
★3.(2019·云南模拟)如图,平行四边形ABCD的对角
线互相垂直,要使ABCD成为正方形,还需添加的一个
条件是__________________________________(只需
添加一个即可)?
∠ABC=90°或AC=BD(答案不唯一)
★★4.如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD, .
(1)求证:AO=EO.
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
解:(1)∵AD∥BC,∴∠CBD=∠ADB,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AB=AD,又∵AE⊥BD,∴BO=DO,又∵∠AOD=∠EOB,∴△AOD≌△EOB,∴AO=EO.
(2)当△ABC满足∠ABC=90°时,四边形ABED是正方形.理由:∵△AOD≌△EOB,∴AD=BE,
又∵AD∥BE,AE⊥BD,∴四边形ABED是菱形,∴当∠ABC=90°时,菱形ABED是正方形,即当△ABC满足∠ABC=90°时,四边形ABED是正方形.
【火眼金睛】
如图,点E,F,M,N分别是正方形ABCD四条边上的点,若AE=BF=CM=DN,则四边形EFMN是什么图形?证明你的结论.
【正解】四边形EFMN是正方形,理由:
∵AE=BF=CM=DN,
∴AN=DM=CF=BE,
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DNM≌△CMF≌△BFE.
∴EF=EN=NM=MF,∠ENA=∠DMN.
∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°,∴∠ENM=90°.
∴四边形EFMN是正方形.
【一题多变】
如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF..
(1)求证:AE=CF.
(2)连接DB交EF于点O,延长OB至点G,使OG=OD,连接EG,FG,判断四边形DEGF是怎样的四边形,并说明理由.
解:(1)∵四边形ABCD是正方形,
∴DA=DC,∠A=∠C=90°,
在△DAE和△DCF中,
∴△DAE≌△DCF,∴AE=CF.
(2)四边形DEGF是菱形,∵△DAE≌△DCF,
∴DE=DF,∵AE=CF,∴BE=BF,
∴DG是EF的垂直平分线,∴GE=GF,
∵OG=OD,DG⊥EF,∴ED=EG,
∴DE=EG=GF=FD,∴四边形DEGF是菱形.
【母题变式】
【变式一】(变换条件与问法)已知:在菱形ABCD中,E,F在BD上,∠ABC=45°,BE=DF=AE,求证:四边形AECF是正方形.
证明:如图,连接AC交BD于点O,
∵四边形ABCD是菱形,∴AO=CO,BO=DO,AC⊥BD,AB=AD,∠ABE= ∠ABC=22.5°.
∵BE=DF,∴OE=OF,
又∵AO=CO,∴四边形AECF是平行四边形,
∵AC⊥BD,∴四边形AECF是菱形,∴AE=AF,
∵AE=BE,∴∠ABE=∠BAE=22.5°,
∴∠AEF=∠ABE+∠BAE=45°,
∵AE=AF,∴∠AEF=∠AFE=45°,
∴∠EAF=90°,∴菱形AECF是正方形.
【变式二】(变换条件与问法)如图,在边长为2的正方形ABCD中,AE⊥DH于E,BF⊥AE于F,CG⊥BF于G,DH⊥CG于H,且∠ABF=∠BCG=∠CDH=∠DAE=30°.
(1)求证:四边形EFGH为正方形.
(2)求正方形EFGH的面积.
解:(1)∵AE⊥DH,DH⊥CG,∴AE∥CG,
同理:BF∥DH,∴四边形EFGH是平行四边形,
∵AE⊥DH,∴∠FEH=90°,
∴平行四边形EFGH是矩形,
∵四边形ABCD是正方形,∴AD=AB,
在△ABF和△DAE中
∴△ABF≌△DAE,∴AF=DE,BF=AE,
∴FG=FE,∴矩形EFGH是正方形.
(2)在Rt△ABF中,∠ABF=30°,AB=2,
∴AF=1,BF= ,
同理:AE= ,∴EF=AE-AF= -1,
∴S正方形EFGH=EF2=( -1)2=4-2 .
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
