四年级下册数学课件 1四则运算 (共54张PPT)人教版
文档属性
| 名称 | 四年级下册数学课件 1四则运算 (共54张PPT)人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-13 20:14:48 | ||
图片预览








文档简介
(共54张PPT)
四则运算
人教版四年级下册
学习内容
1
加、减法的意义和各部分间的关系
2
乘、除法的意义和各部分间的关系
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
开讲啦~
814KM
1142KM
全长1956KM
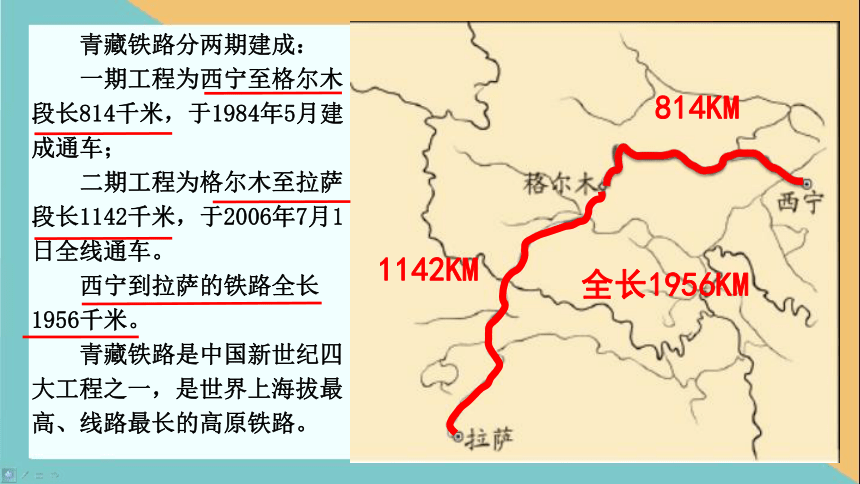
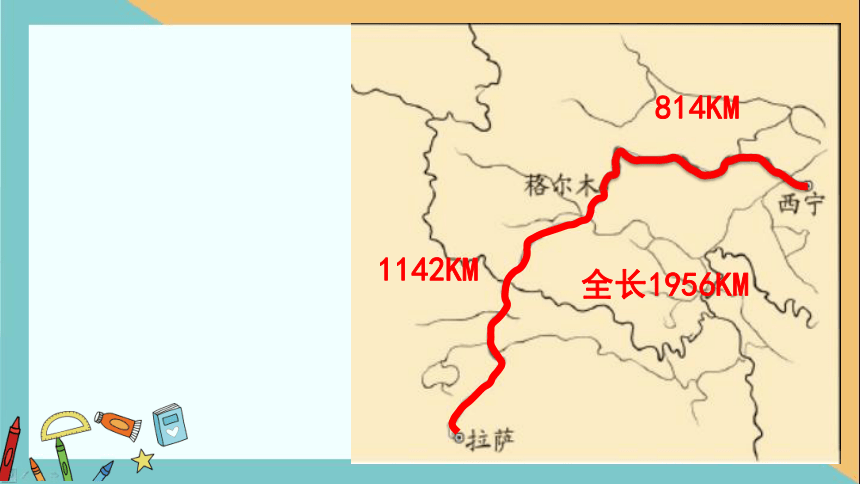
青藏铁路分两期建成:
一期工程为西宁至格尔木段长814千米,于1984年5月建成通车;
二期工程为格尔木至拉萨段长1142千米,于2006年7月1日全线通车。
西宁到拉萨的铁路全长1956千米。
青藏铁路是中国新世纪四大工程之一,是世界上海拔最高、线路最长的高原铁路。
814KM
1142KM
全长1956KM
814KM
1142KM
全长1956KM
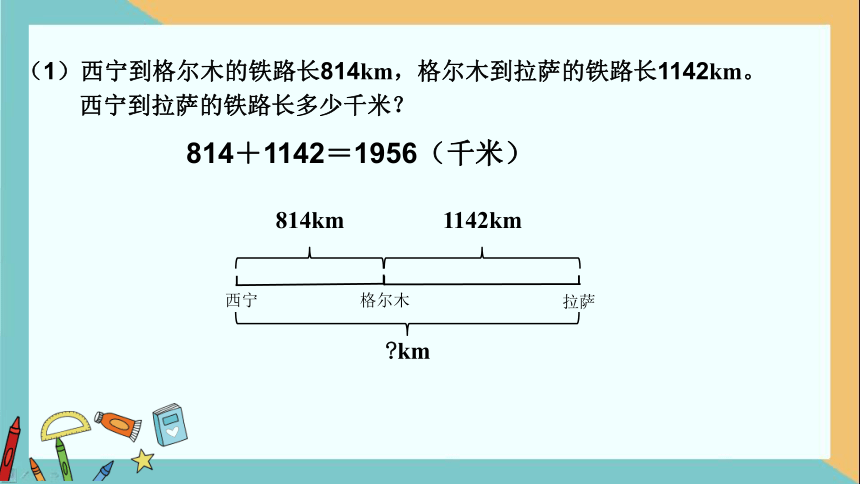
(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。
西宁到拉萨的铁路长多少千米?
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。
格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
814+1142=1956(千米)
1956-814=1142(千米)
1956-1142=814(千米)
?
?km
814km
1142km
西宁
格尔木
拉萨
(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。
西宁到拉萨的铁路长多少千米?
814+1142=1956(千米)
814+1142=1956
把两个数合并成一个数的运算,叫做加法。
加数 + 加数
= 和
加法的意义
(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。
西宁到拉萨的铁路长多少千米?
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。
格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
814
+
1142
=
1956
1956
-
814
=
1142
1956
-
1142
=
814
814
已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
被减数-
减数
=差
+
1142
=
1956
1956
-
814
=
1142
1956
-
1142
=
814
加数+
加数
=和
减法的意义
减法是加法的逆运算。
加、减法的关系
加法各部分间的关系
和=加数+加数
加数=和-另一个加数
814
+
1142
=
1956
1956 - 814
= 1142
( )
( )
1956 - 1142
= 814
减法各部分间的关系
差=被减数-减数
减数=被减数-差
被减数=减数+差
1956
-
814
=
1142
1956 - 1142
= 814
( )
( )
814 + 1142
= 1956
和=加数+加数
加数=和-另一个加数
加法各部分间的关系
差=被减数-减数
减数=被减数-差
被减数=减数+差
减法各部分间的关系
203+147=350
850-239=611
根据加、减法各部分间的关系,写出另外两个等式。
350-147=203
350-203=147
239+611=850
850-611=239
做一做
学习内容
1
2
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
乘、除法的意义和各部分间的关系
开讲啦~
乘、除法的意义和各部分间的关系
用加法算:3+3+3+3=12(枝)
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
12÷3=4(瓶)
12÷4=3(枝)
用乘法算:3×4=12(枝)
?
用加法算:3+3+3+3=12(枝)
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用乘法算:3×4=12(枝)
求几个相同加数的和的简便运算,叫做乘法。
因数×因数
=积
乘法的意义
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
3
×
4
=
12
12
÷
3
=
4
12
÷
4
=
3
3
已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
被除数÷除数
=商
×
4
=
12
12
÷
3
=
4
12
÷
4
=
3
因数×
因数
=积
除法的意义
除法是乘法的逆运算。
乘、除法的关系
积=因数×因数
因数=积÷另一个因数
乘法各部分间的关系
商=被除数÷除数
除数=被除数÷商被除数=商×除数
除法各部分间的关系
30÷4=7……2
被除数=除数×商+余数
除法各部分间的关系
4×7+2
=28+2
=30
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
你知道有关0的哪些运算?具体描述一下这些运算。
有关0的运算
加法:一个数加上0,还得原数。
请你举一些有关0的运算,说说你发现了什么?
有关0的运算
减法:一个数减0,还得这个数。
被减数和减数相等,差是0。
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
请你举一些有关0的运算,说说你发现了什么?
有关0的运算
乘法:一个数和0相乘,仍得0。
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
请你举一些有关0的运算,说说你发现了什么?
有关0的运算
除法:0除以一个非0的数,还得0。
注意:0不能做除数。
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
注意:0不能做除数。
5÷0=( )
有关0的运算
想:( )×0=5
注意:0不能做除数。
0÷0=( )
有关0的运算
想:( )×0=0
有关0的运算
除法:0除以一个非0的数,还得0。
加法:一个数加上0,还得原数。
乘法:一个数和0相乘,仍得0。
减法:一个数减0,还得这个数。
被减数和减数相等,差是0。
注意:0不能做除数。
总结提升
总结提升
四则运算的意义
四则运算 意义 算式各部分名称
加法
减法
乘法
除法
四则运算的意义
四则运算 意义 算式各部分名称
加法 把两个数合并成一个数的运算 加数+加数=和
减法 已知两个数的和与其中一个加数,求另一个加数的运算 被减数-减数=差
乘法 求几个相同加数的和的简便运算 因数×因数=积
除法 已知两个数的积与其中一个因数,求另一个因数的运算 被除数÷除数=商……余数
总结提升
加法
减法
乘法
除法
逆运算
逆运算
求几个相同加数和的简便运算
四则运算间的关系
总结提升
学习内容
1
2
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
乘、除法的意义和各部分间的关系
四则混合运算的顺序
开讲啦~
前置作业
53-24+38
15÷3×5
7+4×3
7×(7-5)
在没有括号的算式里,只有加减法或只有乘除法,都要____________按顺序计算。
在没有括号的算式里,如果有乘除法,又有加减法,要先算________,后算_________。
算式里有括号的,要先算____________的。
先说一说下面各题的运算顺序,再计算
96÷12+4×2
=8+8
=16
( )
96÷12+4×2
=96÷16×2
=6×2
=12
[ ]
=96÷[16×2]
=96÷32
=3
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
96÷(12+4)×2
先说一说下面各题的运算顺序,再计算。
360÷(70-4×16)
=360÷(70-64)
=360÷6
=60
158×[(27+54)÷9]
=158× [81÷9]
=158×9
=1422
做一做
四则混合运算
算式里有括号
算式里没有括号
只有加、减法或只有乘、除法
有乘、除法,又有加、减法
只有小括号
有小括号和中括号
从左往右
先乘除,后加减
总结提升
学习内容
1
2
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
乘、除法的意义和各部分间的关系
解决问题
开讲啦~
怎样租船最省钱?
分析思考
大船:30÷6=5(元)
小船:24÷4=6(元)
5元<6元
1
租哪种船更便宜?
租大船便宜
分析思考
30×5+24
=150+24
=174(元)
空2个座位
方案一:
5条大船,1条小船。
32÷6=5(条)……2(人)
分析思考
如果不空座位会不会更省钱?
30×4+24×2
=120+48
=168(元)
方案二:
4条大船,2条小船。
2
分析思考
30×4+24×2
=120+48
=168(元)
方案二:
4条大船,2条小船。
30×5+24
=150+24
=174(元)
方案一:
5条大船,1条小船。
174元>168元
答:租4条大船和2条小船最省钱。
回顾反思
解决这类问题需要注意什么呢?
租哪种船便宜
不空座位
祝学习愉快!
四则运算
人教版四年级下册
学习内容
1
加、减法的意义和各部分间的关系
2
乘、除法的意义和各部分间的关系
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
开讲啦~
814KM
1142KM
全长1956KM
青藏铁路分两期建成:
一期工程为西宁至格尔木段长814千米,于1984年5月建成通车;
二期工程为格尔木至拉萨段长1142千米,于2006年7月1日全线通车。
西宁到拉萨的铁路全长1956千米。
青藏铁路是中国新世纪四大工程之一,是世界上海拔最高、线路最长的高原铁路。
814KM
1142KM
全长1956KM
814KM
1142KM
全长1956KM
(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。
西宁到拉萨的铁路长多少千米?
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。
格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
814+1142=1956(千米)
1956-814=1142(千米)
1956-1142=814(千米)
?
?km
814km
1142km
西宁
格尔木
拉萨
(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。
西宁到拉萨的铁路长多少千米?
814+1142=1956(千米)
814+1142=1956
把两个数合并成一个数的运算,叫做加法。
加数 + 加数
= 和
加法的意义
(1)西宁到格尔木的铁路长814km,格尔木到拉萨的铁路长1142km。
西宁到拉萨的铁路长多少千米?
(2)西宁到拉萨的铁路全长1956km,其中西宁到格尔木814km。
格尔木到拉萨的铁路长多少千米?
(3)西宁到拉萨的铁路全长1956km,其中格尔木到拉萨长1142km。
西宁到格尔木的铁路长多少千米?
814
+
1142
=
1956
1956
-
814
=
1142
1956
-
1142
=
814
814
已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
被减数-
减数
=差
+
1142
=
1956
1956
-
814
=
1142
1956
-
1142
=
814
加数+
加数
=和
减法的意义
减法是加法的逆运算。
加、减法的关系
加法各部分间的关系
和=加数+加数
加数=和-另一个加数
814
+
1142
=
1956
1956 - 814
= 1142
( )
( )
1956 - 1142
= 814
减法各部分间的关系
差=被减数-减数
减数=被减数-差
被减数=减数+差
1956
-
814
=
1142
1956 - 1142
= 814
( )
( )
814 + 1142
= 1956
和=加数+加数
加数=和-另一个加数
加法各部分间的关系
差=被减数-减数
减数=被减数-差
被减数=减数+差
减法各部分间的关系
203+147=350
850-239=611
根据加、减法各部分间的关系,写出另外两个等式。
350-147=203
350-203=147
239+611=850
850-611=239
做一做
学习内容
1
2
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
乘、除法的意义和各部分间的关系
开讲啦~
乘、除法的意义和各部分间的关系
用加法算:3+3+3+3=12(枝)
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
12÷3=4(瓶)
12÷4=3(枝)
用乘法算:3×4=12(枝)
?
用加法算:3+3+3+3=12(枝)
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
用乘法算:3×4=12(枝)
求几个相同加数的和的简便运算,叫做乘法。
因数×因数
=积
乘法的意义
(3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
(2)有12枝花,每3枝插一瓶,可以插几瓶?
(1)每个花瓶里插3枝花,4个花瓶一共插了多少枝花?
3
×
4
=
12
12
÷
3
=
4
12
÷
4
=
3
3
已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
被除数÷除数
=商
×
4
=
12
12
÷
3
=
4
12
÷
4
=
3
因数×
因数
=积
除法的意义
除法是乘法的逆运算。
乘、除法的关系
积=因数×因数
因数=积÷另一个因数
乘法各部分间的关系
商=被除数÷除数
除数=被除数÷商被除数=商×除数
除法各部分间的关系
30÷4=7……2
被除数=除数×商+余数
除法各部分间的关系
4×7+2
=28+2
=30
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
你知道有关0的哪些运算?具体描述一下这些运算。
有关0的运算
加法:一个数加上0,还得原数。
请你举一些有关0的运算,说说你发现了什么?
有关0的运算
减法:一个数减0,还得这个数。
被减数和减数相等,差是0。
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
请你举一些有关0的运算,说说你发现了什么?
有关0的运算
乘法:一个数和0相乘,仍得0。
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
请你举一些有关0的运算,说说你发现了什么?
有关0的运算
除法:0除以一个非0的数,还得0。
注意:0不能做除数。
24+0=24 70-0=70 0×8=0 0÷9=0
0+504=504 13-13=0 392×0=0 0÷36=0
注意:0不能做除数。
5÷0=( )
有关0的运算
想:( )×0=5
注意:0不能做除数。
0÷0=( )
有关0的运算
想:( )×0=0
有关0的运算
除法:0除以一个非0的数,还得0。
加法:一个数加上0,还得原数。
乘法:一个数和0相乘,仍得0。
减法:一个数减0,还得这个数。
被减数和减数相等,差是0。
注意:0不能做除数。
总结提升
总结提升
四则运算的意义
四则运算 意义 算式各部分名称
加法
减法
乘法
除法
四则运算的意义
四则运算 意义 算式各部分名称
加法 把两个数合并成一个数的运算 加数+加数=和
减法 已知两个数的和与其中一个加数,求另一个加数的运算 被减数-减数=差
乘法 求几个相同加数的和的简便运算 因数×因数=积
除法 已知两个数的积与其中一个因数,求另一个因数的运算 被除数÷除数=商……余数
总结提升
加法
减法
乘法
除法
逆运算
逆运算
求几个相同加数和的简便运算
四则运算间的关系
总结提升
学习内容
1
2
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
乘、除法的意义和各部分间的关系
四则混合运算的顺序
开讲啦~
前置作业
53-24+38
15÷3×5
7+4×3
7×(7-5)
在没有括号的算式里,只有加减法或只有乘除法,都要____________按顺序计算。
在没有括号的算式里,如果有乘除法,又有加减法,要先算________,后算_________。
算式里有括号的,要先算____________的。
先说一说下面各题的运算顺序,再计算
96÷12+4×2
=8+8
=16
( )
96÷12+4×2
=96÷16×2
=6×2
=12
[ ]
=96÷[16×2]
=96÷32
=3
一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
96÷(12+4)×2
先说一说下面各题的运算顺序,再计算。
360÷(70-4×16)
=360÷(70-64)
=360÷6
=60
158×[(27+54)÷9]
=158× [81÷9]
=158×9
=1422
做一做
四则混合运算
算式里有括号
算式里没有括号
只有加、减法或只有乘、除法
有乘、除法,又有加、减法
只有小括号
有小括号和中括号
从左往右
先乘除,后加减
总结提升
学习内容
1
2
3
四则混合运算的顺序
4
解决问题
加、减法的意义和各部分间的关系
乘、除法的意义和各部分间的关系
解决问题
开讲啦~
怎样租船最省钱?
分析思考
大船:30÷6=5(元)
小船:24÷4=6(元)
5元<6元
1
租哪种船更便宜?
租大船便宜
分析思考
30×5+24
=150+24
=174(元)
空2个座位
方案一:
5条大船,1条小船。
32÷6=5(条)……2(人)
分析思考
如果不空座位会不会更省钱?
30×4+24×2
=120+48
=168(元)
方案二:
4条大船,2条小船。
2
分析思考
30×4+24×2
=120+48
=168(元)
方案二:
4条大船,2条小船。
30×5+24
=150+24
=174(元)
方案一:
5条大船,1条小船。
174元>168元
答:租4条大船和2条小船最省钱。
回顾反思
解决这类问题需要注意什么呢?
租哪种船便宜
不空座位
祝学习愉快!
