13.2 全反射导学案word版无答案
文档属性
| 名称 | 13.2 全反射导学案word版无答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 290.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-13 18:35:39 | ||
图片预览

文档简介
1
13.2 全反射
一、全反射
1.光疏介质和光密介质
(1)光疏介质:折射率较 (填“大”或“小”)的介质.
(2)光密介质:折射率较 (填“大”或“小”)的介质.
(3)光疏介质与光密介质是 (填“相对”或“绝对”)的.
2.全反射现象
(1)全反射:光从光密介质射入光疏介质时,同时发生折射和反射.若入射角增大到某一角度, 光线完全消失,
只剩下 光线的现象.
(2)临界角:刚好发生全反射,即折射角等于 时的入射角.用字母 C表示,光从介质射入空气(真空)时,发生
全反射的临界角 C与介质的折射率 n的关系是 .
(3)全反射发生的条件
①光从 介质射入 介质.
②入射角 临界角.
二、全反射棱镜
1.形状:截面为 三角形的棱镜.
2.全反射棱镜的特点
(1)当光垂直于它的一个界面射入后,都会在其内部发生 ,与平面镜相比,它的反射率很高.
(2)反射面不必涂敷任何反光物质,反射时失真 .
三、光导纤维
1.原理:利用了光的 .
2.构造:由内芯和外套两层组成.内芯的折射率比外套的 ,光传播时在内芯与外套的界面上发生 .
3.光纤通信的优点是容量 、衰减 、抗干扰性强等.
4.光导纤维除应用于光纤通信外,还可应用于医学上的内窥镜等.
一、全反射
当光从水中射向与玻璃的交界面时,只要入射角足够大就会发生全反射,这种说法正确吗?为什么?
1.全反射现象
(1)全反射的条件:
①光由光 介质射入光 介质.
②入射角 临界角.
(2)全反射遵循的规律:①发生全反射时,光全部返回原介质,入射光与反射光遵循光的反射定律.
②全反射的临界角 C和折射率 n的关系: .
(3)从能量角度来理解全反射:当光从光密介质射入光疏介质时,随着入射角增大,折射角也 .同时折射光线
强度减弱,能量 ,反射光线强度增强,能量 ,当入射角达到临界角时,折射光线强度减弱到 ,反射光
线的能量 入射光线的能量.
2
2.不同色光的临界角:由于不同颜色(频率不同)的光在同一介质中的折射率不同.频率越大的光,折射率也 ,
所以不同颜色的光由同一介质射向空气或真空时,频率越大的光的临界角越小,越 发生全反射.
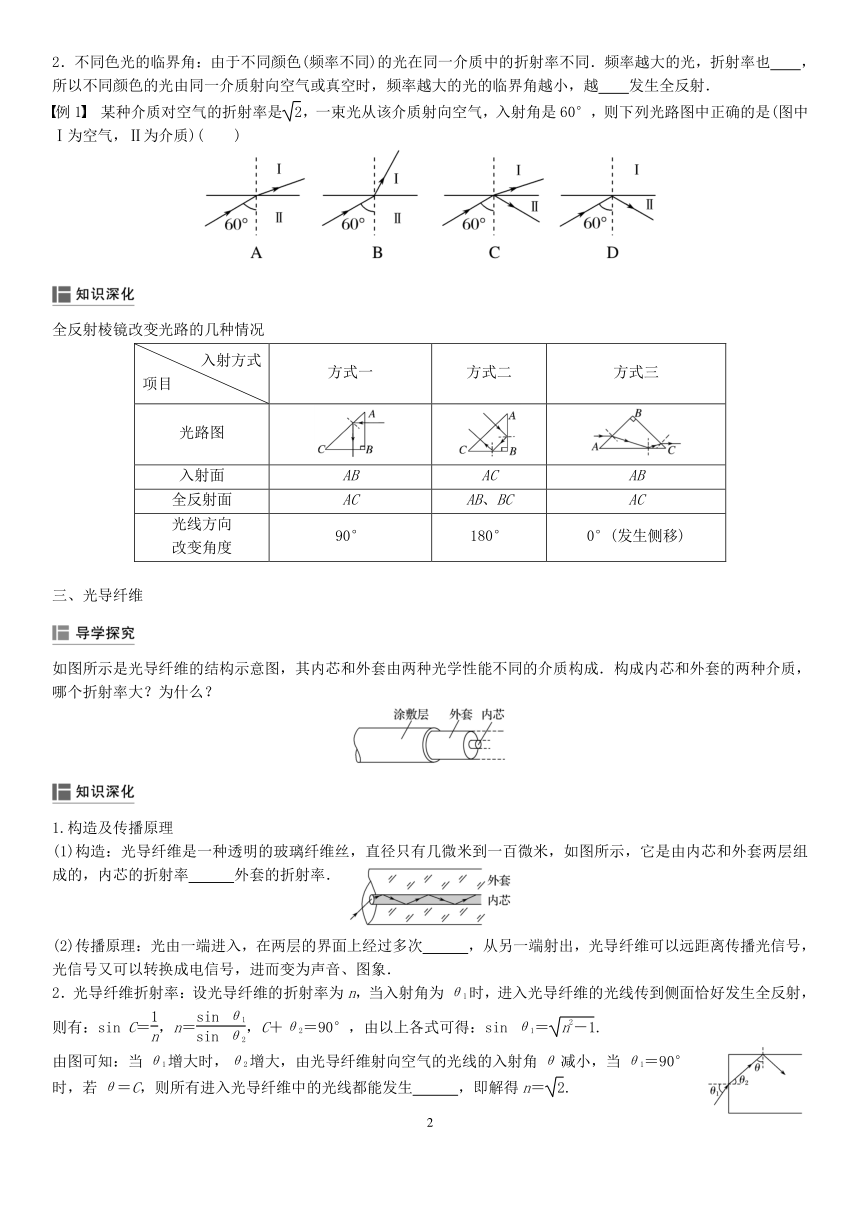
例 1 某种介质对空气的折射率是 2,一束光从该介质射向空气,入射角是 60°,则下列光路图中正确的是(图中
Ⅰ为空气,Ⅱ为介质)( )
全反射棱镜改变光路的几种情况
入射方式
项目
方式一 方式二 方式三
光路图
入射面 AB AC AB
全反射面 AC AB、BC AC
光线方向
改变角度
90° 180° 0°(发生侧移)
三、光导纤维
如图所示是光导纤维的结构示意图,其内芯和外套由两种光学性能不同的介质构成.构成内芯和外套的两种介质,
哪个折射率大?为什么?
1.构造及传播原理
(1)构造:光导纤维是一种透明的玻璃纤维丝,直径只有几微米到一百微米,如图所示,它是由内芯和外套两层组
成的,内芯的折射率 外套的折射率.
(2)传播原理:光由一端进入,在两层的界面上经过多次 ,从另一端射出,光导纤维可以远距离传播光信号,
光信号又可以转换成电信号,进而变为声音、图象.
2.光导纤维折射率:设光导纤维的折射率为 n,当入射角为θ1时,进入光导纤维的光线传到侧面恰好发生全反射,
则有:sin C=
1
n
,n=
sin θ1
sin θ2
,C+θ2=90°,由以上各式可得:sin θ1= n
2
-1.
由图可知:当θ1增大时,θ2增大,由光导纤维射向空气的光线的入射角 θ减小,当θ1=90°
时,若 θ=C,则所有进入光导纤维中的光线都能发生 ,即解得 n= 2.
3
以上是光从光导纤维射向真空时得到的折射率,由于光导纤维包有外套,外套的折射率比真空的折射率 ,因
此折射率要比 2大些.
四、全反射的应用
解决全反射问题的思路
(1)确定光是由光疏介质进入光密介质还是由光密介质进入光疏介质.
(2)若光由介质进入空气(真空)时,则根据 确定临界角,看是否发生 .
(3)根据题设条件,画出入射角 临界角的“临界光路”.
(4)运用几何关系、三角函数关系、反射定律等进行判断推理、运算及变换并进行动态分析或定量计算.
一.选择题(共 6 小题)
1.如图所示,夏天,在平静无风的海面上,向远方望去,有时能看到山峰、船舶、楼台、亭阁、集市、庙宇等出
现在远方的空中.沙漠里有时也会看到远处的水源、仙人掌近在咫尺,可望而不可及,这就是“蜃景”.下列说
法中错误的是( )
A.海面上上层空气的折射率比下层空气的折射率要 B.沙面上上层空气的折射率比下层空气的折射率要小
C.A是蜃景,B是景物 D.C是蜃景,D是景物
2.如图所示的长直光纤,柱芯为玻璃,外层以折射率较玻璃为低的介质包覆.若光线自光纤左端进入,与中心轴
的夹角为θ,则下列有关此光线传递方式的叙述正确的是( )
A.不论 θ为何值,光线都不会发生全反射 B.不论 θ为何值,光线都会发生全反射
C.θ足够小时,光线才会发生全反射 D.0足够大时,光线才会发生全反射
3.图示为一横截面为等腰直角三角形的三棱镜,光线 O 从它的一直角垂直射入,其对光线 O 的临界角为 40°,关
于图中画出的 a、b、c 三条光线,说法正确的是( )
A.a是光线 O的出射光 B.b是光线 O的出射光
C.c是光线 O的出射光 D.a、b、c都不是光线 O的出射光
4.a、b 两种单色光以相同的入射角从空气斜射向某种玻璃中,光路如图所示.关于 a、b两种单色光,下列说法中
正确的是( )
A.该种玻璃对 a光的折射率较大
B.b光在该玻璃中传播时的速度较大
C.a光的频率较小
D.两种单色光从该玻璃中射入空气发生全反射时,a光的临界角较小
4
5.如图所示,已知介质Ⅱ为空气,介质Ⅰ的折射率为 ,则下列说法中正确的是( )
A.光线 a、b都不能发生全反射
B.光线 a、b都能发生全反射
C.光线 a发生全反射,光线 b不发生全反射
D.光线 a不发生全反射,光线 b发生全反射
6.如图所示,让光沿着半圆形玻璃砖的半径射到它的平直的边上,在这个边与空气的界面上会发生反射和折射。
逐渐增大入射角,观察反射光线和折射光线的变化。关于该实验现象,下列说法正确的是( )
A.反射光线和折射光线都沿顺时针方向转动
B.反射光线和折射光线转过的角度相同
C.在还未发生全反射过程中,反射光越来越强
D.最终反射光完全消失
二.多选题(共 1小题)
7.图中的等腰直角三角形表示三棱镜,光线垂直于一个面入射,在底面上发生全反射,由此看出棱镜的折射率可
能是( )
A.1.7 B.1.8 C.1.5 D.1.36
三.填空题(共 1小题)
8.如图,三角形 ABC为某透明介质的横截面,O为 BC边的中点,位于截面所在平面内的一束光线自 O以角 I入射,
第一次到达 AB边恰好发生全反射,已知θ=15°,BC边长为 2L,该介质的折射率为 ,求:
(i)入射角 i;
(ii)从入射角到发生第一次全反射所用的时间(设光在真空中的速度为 v,可能用到 sin75°= 或
sin15°= )
四.计算题(共 1小题)
9.如图所示,某 L 形透明材料的折射率 n=2.现沿 AB 方向切去一角,AB与水平方向的夹角为 θ.为使水平方向
的光线射到 AB面时不会射入空气,求 θ的最大值。
13.2 全反射
一、全反射
1.光疏介质和光密介质
(1)光疏介质:折射率较 (填“大”或“小”)的介质.
(2)光密介质:折射率较 (填“大”或“小”)的介质.
(3)光疏介质与光密介质是 (填“相对”或“绝对”)的.
2.全反射现象
(1)全反射:光从光密介质射入光疏介质时,同时发生折射和反射.若入射角增大到某一角度, 光线完全消失,
只剩下 光线的现象.
(2)临界角:刚好发生全反射,即折射角等于 时的入射角.用字母 C表示,光从介质射入空气(真空)时,发生
全反射的临界角 C与介质的折射率 n的关系是 .
(3)全反射发生的条件
①光从 介质射入 介质.
②入射角 临界角.
二、全反射棱镜
1.形状:截面为 三角形的棱镜.
2.全反射棱镜的特点
(1)当光垂直于它的一个界面射入后,都会在其内部发生 ,与平面镜相比,它的反射率很高.
(2)反射面不必涂敷任何反光物质,反射时失真 .
三、光导纤维
1.原理:利用了光的 .
2.构造:由内芯和外套两层组成.内芯的折射率比外套的 ,光传播时在内芯与外套的界面上发生 .
3.光纤通信的优点是容量 、衰减 、抗干扰性强等.
4.光导纤维除应用于光纤通信外,还可应用于医学上的内窥镜等.
一、全反射
当光从水中射向与玻璃的交界面时,只要入射角足够大就会发生全反射,这种说法正确吗?为什么?
1.全反射现象
(1)全反射的条件:
①光由光 介质射入光 介质.
②入射角 临界角.
(2)全反射遵循的规律:①发生全反射时,光全部返回原介质,入射光与反射光遵循光的反射定律.
②全反射的临界角 C和折射率 n的关系: .
(3)从能量角度来理解全反射:当光从光密介质射入光疏介质时,随着入射角增大,折射角也 .同时折射光线
强度减弱,能量 ,反射光线强度增强,能量 ,当入射角达到临界角时,折射光线强度减弱到 ,反射光
线的能量 入射光线的能量.
2
2.不同色光的临界角:由于不同颜色(频率不同)的光在同一介质中的折射率不同.频率越大的光,折射率也 ,
所以不同颜色的光由同一介质射向空气或真空时,频率越大的光的临界角越小,越 发生全反射.
例 1 某种介质对空气的折射率是 2,一束光从该介质射向空气,入射角是 60°,则下列光路图中正确的是(图中
Ⅰ为空气,Ⅱ为介质)( )
全反射棱镜改变光路的几种情况
入射方式
项目
方式一 方式二 方式三
光路图
入射面 AB AC AB
全反射面 AC AB、BC AC
光线方向
改变角度
90° 180° 0°(发生侧移)
三、光导纤维
如图所示是光导纤维的结构示意图,其内芯和外套由两种光学性能不同的介质构成.构成内芯和外套的两种介质,
哪个折射率大?为什么?
1.构造及传播原理
(1)构造:光导纤维是一种透明的玻璃纤维丝,直径只有几微米到一百微米,如图所示,它是由内芯和外套两层组
成的,内芯的折射率 外套的折射率.
(2)传播原理:光由一端进入,在两层的界面上经过多次 ,从另一端射出,光导纤维可以远距离传播光信号,
光信号又可以转换成电信号,进而变为声音、图象.
2.光导纤维折射率:设光导纤维的折射率为 n,当入射角为θ1时,进入光导纤维的光线传到侧面恰好发生全反射,
则有:sin C=
1
n
,n=
sin θ1
sin θ2
,C+θ2=90°,由以上各式可得:sin θ1= n
2
-1.
由图可知:当θ1增大时,θ2增大,由光导纤维射向空气的光线的入射角 θ减小,当θ1=90°
时,若 θ=C,则所有进入光导纤维中的光线都能发生 ,即解得 n= 2.
3
以上是光从光导纤维射向真空时得到的折射率,由于光导纤维包有外套,外套的折射率比真空的折射率 ,因
此折射率要比 2大些.
四、全反射的应用
解决全反射问题的思路
(1)确定光是由光疏介质进入光密介质还是由光密介质进入光疏介质.
(2)若光由介质进入空气(真空)时,则根据 确定临界角,看是否发生 .
(3)根据题设条件,画出入射角 临界角的“临界光路”.
(4)运用几何关系、三角函数关系、反射定律等进行判断推理、运算及变换并进行动态分析或定量计算.
一.选择题(共 6 小题)
1.如图所示,夏天,在平静无风的海面上,向远方望去,有时能看到山峰、船舶、楼台、亭阁、集市、庙宇等出
现在远方的空中.沙漠里有时也会看到远处的水源、仙人掌近在咫尺,可望而不可及,这就是“蜃景”.下列说
法中错误的是( )
A.海面上上层空气的折射率比下层空气的折射率要 B.沙面上上层空气的折射率比下层空气的折射率要小
C.A是蜃景,B是景物 D.C是蜃景,D是景物
2.如图所示的长直光纤,柱芯为玻璃,外层以折射率较玻璃为低的介质包覆.若光线自光纤左端进入,与中心轴
的夹角为θ,则下列有关此光线传递方式的叙述正确的是( )
A.不论 θ为何值,光线都不会发生全反射 B.不论 θ为何值,光线都会发生全反射
C.θ足够小时,光线才会发生全反射 D.0足够大时,光线才会发生全反射
3.图示为一横截面为等腰直角三角形的三棱镜,光线 O 从它的一直角垂直射入,其对光线 O 的临界角为 40°,关
于图中画出的 a、b、c 三条光线,说法正确的是( )
A.a是光线 O的出射光 B.b是光线 O的出射光
C.c是光线 O的出射光 D.a、b、c都不是光线 O的出射光
4.a、b 两种单色光以相同的入射角从空气斜射向某种玻璃中,光路如图所示.关于 a、b两种单色光,下列说法中
正确的是( )
A.该种玻璃对 a光的折射率较大
B.b光在该玻璃中传播时的速度较大
C.a光的频率较小
D.两种单色光从该玻璃中射入空气发生全反射时,a光的临界角较小
4
5.如图所示,已知介质Ⅱ为空气,介质Ⅰ的折射率为 ,则下列说法中正确的是( )
A.光线 a、b都不能发生全反射
B.光线 a、b都能发生全反射
C.光线 a发生全反射,光线 b不发生全反射
D.光线 a不发生全反射,光线 b发生全反射
6.如图所示,让光沿着半圆形玻璃砖的半径射到它的平直的边上,在这个边与空气的界面上会发生反射和折射。
逐渐增大入射角,观察反射光线和折射光线的变化。关于该实验现象,下列说法正确的是( )
A.反射光线和折射光线都沿顺时针方向转动
B.反射光线和折射光线转过的角度相同
C.在还未发生全反射过程中,反射光越来越强
D.最终反射光完全消失
二.多选题(共 1小题)
7.图中的等腰直角三角形表示三棱镜,光线垂直于一个面入射,在底面上发生全反射,由此看出棱镜的折射率可
能是( )
A.1.7 B.1.8 C.1.5 D.1.36
三.填空题(共 1小题)
8.如图,三角形 ABC为某透明介质的横截面,O为 BC边的中点,位于截面所在平面内的一束光线自 O以角 I入射,
第一次到达 AB边恰好发生全反射,已知θ=15°,BC边长为 2L,该介质的折射率为 ,求:
(i)入射角 i;
(ii)从入射角到发生第一次全反射所用的时间(设光在真空中的速度为 v,可能用到 sin75°= 或
sin15°= )
四.计算题(共 1小题)
9.如图所示,某 L 形透明材料的折射率 n=2.现沿 AB 方向切去一角,AB与水平方向的夹角为 θ.为使水平方向
的光线射到 AB面时不会射入空气,求 θ的最大值。
