3.1.1 空间向量及其加减运算 课件 21张PPT
文档属性
| 名称 | 3.1.1 空间向量及其加减运算 课件 21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 260.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
高中数学 选修2-1
第三章 空间向量与立体几何
3.1 空间向量及其运算
3.1.1 空间向量及其加减运算
一、平面向量复习
⒈定义:
既有大小又有方向的量叫向量.
几何表示法:
用有向线段表示;
字母表示法:
用字母a、b等或者用有向线段
的起点与终点字母 表示.
相等的向量:
长度相等且方向相同的向量.
A
B
C
D
⒉平面向量的加减法运算
⑴向量的加法:
a
b
a+b
平行四边形法则
a
b
a+b
三角形法则(首尾相连)
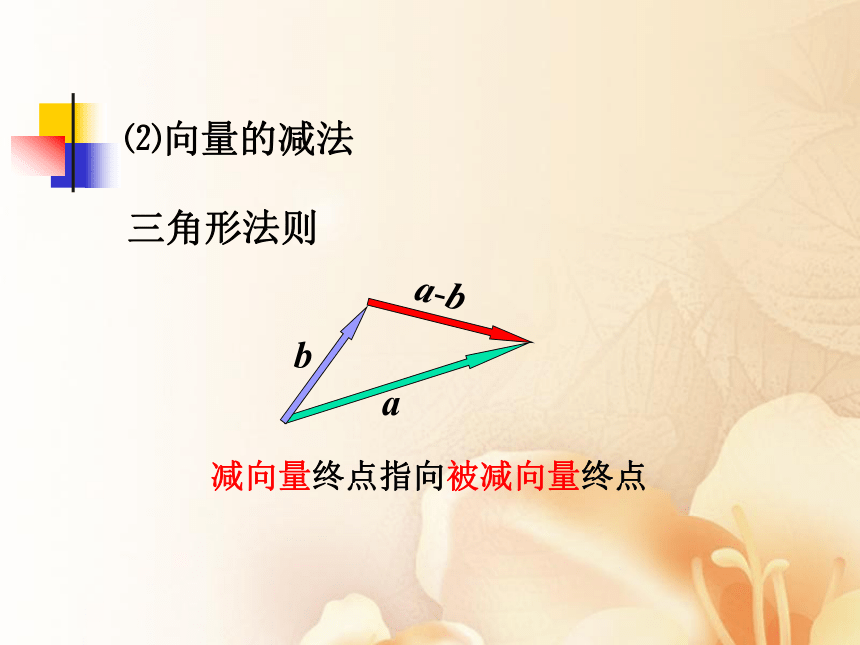
⑵向量的减法
a
b
a-b
三角形法则
减向量终点指向被减向量终点
⒊平面向量的加法运算律
加法交换律:
a+b=b+a
加法结合律:
(a+b)+c=a+(b+c)
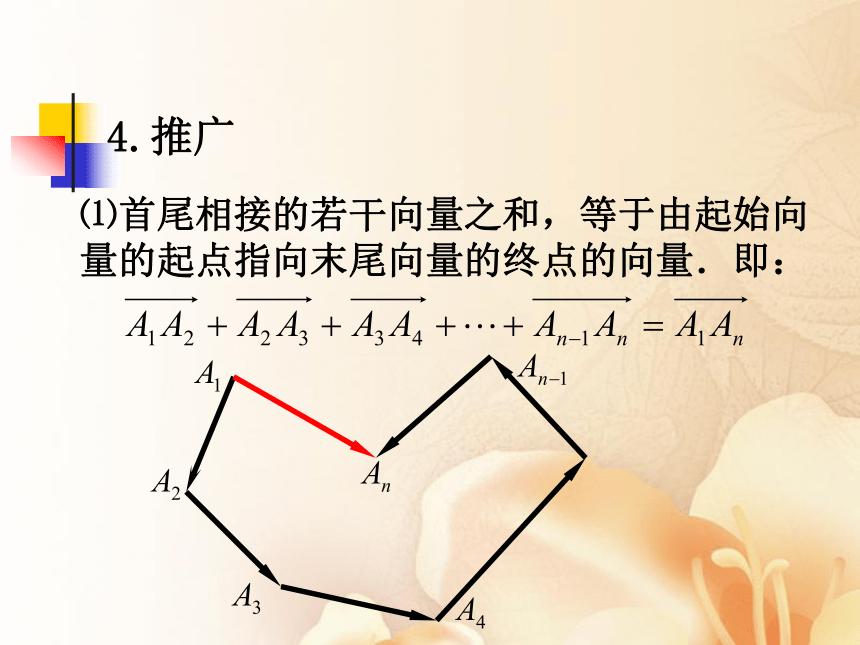
4.推广
⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
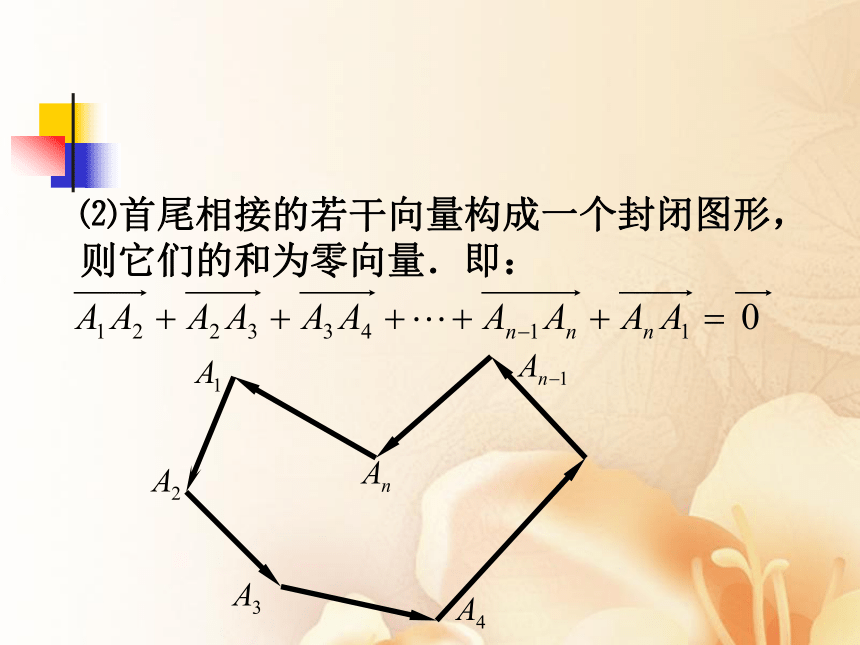
⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
二、空间向量及其加减运算
⒈空间向量:
空间中具有大小和方向的量叫做向量.
⑴定义:
⑵表示方法:
①空间向量的表示方法和平面向量一样;
③空间任意两个向量都可以用同一平面
内的两条有向线段表示.
②同向且等长的有向线段表示同一向量或
相等的向量;
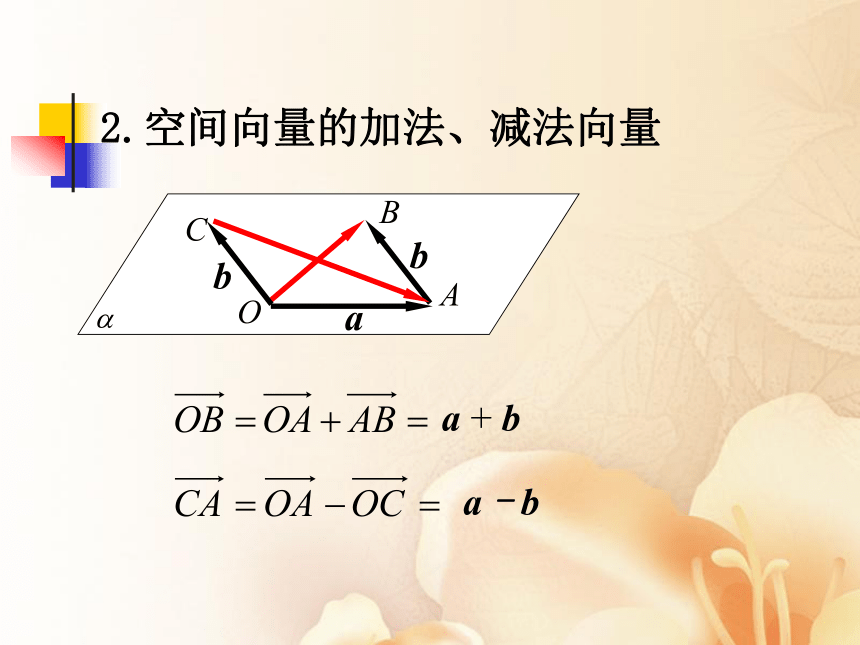
2.空间向量的加法、减法向量
a + b
a
b
A
B
b
C
O
a - b
⒊空间向量加法运算律
⑴加法交换律:
a + b = b + a;
⑵加法结合律:
(a + b) + c =a + (b + c);
a
b
c
a + b + c
a
b
c
a + b + c
a + b
b + c
对空间向量的加法、减法的说明:
⒈空间向量的运算就是平面向量运算的推广.
⒉两个向量相加的平行四边形法则在空间仍
然成立.
⒊空间向量的加法运算可以推广至若干个向
量相加.
4.推广
⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
例1、给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是( )
A.1 B.2 C.3 D.4
三、典例剖析:
A
B
C
D
A
B
C
D
A1
B1
C1
D1
a
平行四边形ABCD按向量 平移
到A1B1C1D1的轨迹所形成的几何体.
a
记做ABCD-A1B1C1D1
注:始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量
平行六面体:
解:
A
B
C
D
A'
B'
C'
D'
始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量
A
B
C
D
A'
B'
C'
D'
例2、
例3、在如图所示的平行六面体中,
求证:
A
B
C
D
A'
B'
C'
D'
变式:
已知平行六面体 则下列四式中:
其中正确的是 。
②
③
①
A
B
C
D
A'
B'
C'
D'
平面向量
概念
加法
减法
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量
具有大小和方向的量
加法交换律
加法结合律
四、小结
加法交换律
加法结合律
类比、数形结合
1、课本86页练习2、3;
2、预习3.1.2空间向量的数乘运算。
五、课后作业:
高中数学 选修2-1
第三章 空间向量与立体几何
3.1 空间向量及其运算
3.1.1 空间向量及其加减运算
一、平面向量复习
⒈定义:
既有大小又有方向的量叫向量.
几何表示法:
用有向线段表示;
字母表示法:
用字母a、b等或者用有向线段
的起点与终点字母 表示.
相等的向量:
长度相等且方向相同的向量.
A
B
C
D
⒉平面向量的加减法运算
⑴向量的加法:
a
b
a+b
平行四边形法则
a
b
a+b
三角形法则(首尾相连)
⑵向量的减法
a
b
a-b
三角形法则
减向量终点指向被减向量终点
⒊平面向量的加法运算律
加法交换律:
a+b=b+a
加法结合律:
(a+b)+c=a+(b+c)
4.推广
⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
二、空间向量及其加减运算
⒈空间向量:
空间中具有大小和方向的量叫做向量.
⑴定义:
⑵表示方法:
①空间向量的表示方法和平面向量一样;
③空间任意两个向量都可以用同一平面
内的两条有向线段表示.
②同向且等长的有向线段表示同一向量或
相等的向量;
2.空间向量的加法、减法向量
a + b
a
b
A
B
b
C
O
a - b
⒊空间向量加法运算律
⑴加法交换律:
a + b = b + a;
⑵加法结合律:
(a + b) + c =a + (b + c);
a
b
c
a + b + c
a
b
c
a + b + c
a + b
b + c
对空间向量的加法、减法的说明:
⒈空间向量的运算就是平面向量运算的推广.
⒉两个向量相加的平行四边形法则在空间仍
然成立.
⒊空间向量的加法运算可以推广至若干个向
量相加.
4.推广
⑴首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.即:
⑵首尾相接的若干向量构成一个封闭图形,则它们的和为零向量.即:
例1、给出以下命题:
(1)两个空间向量相等,则它们的起点、终点相同;
(2)若空间向量 满足 ,则 ;
(3)在正方体 中,必有 ;
(4)若空间向量 满足 ,则 ;
(5)空间中任意两个单位向量必相等。
其中不正确命题的个数是( )
A.1 B.2 C.3 D.4
三、典例剖析:
A
B
C
D
A
B
C
D
A1
B1
C1
D1
a
平行四边形ABCD按向量 平移
到A1B1C1D1的轨迹所形成的几何体.
a
记做ABCD-A1B1C1D1
注:始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量
平行六面体:
解:
A
B
C
D
A'
B'
C'
D'
始点相同的三个不共面向量之和,等于以这三个向量
为棱的平行六面体的以公共始点为始点的对角线所示向量
A
B
C
D
A'
B'
C'
D'
例2、
例3、在如图所示的平行六面体中,
求证:
A
B
C
D
A'
B'
C'
D'
变式:
已知平行六面体 则下列四式中:
其中正确的是 。
②
③
①
A
B
C
D
A'
B'
C'
D'
平面向量
概念
加法
减法
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量
具有大小和方向的量
加法交换律
加法结合律
四、小结
加法交换律
加法结合律
类比、数形结合
1、课本86页练习2、3;
2、预习3.1.2空间向量的数乘运算。
五、课后作业:
