3.1.3 空间向量的数量积运算 课件 19张PPT
文档属性
| 名称 | 3.1.3 空间向量的数量积运算 课件 19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 849.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
3.1.3空间向量的数量积运算
1.空间向量的加减法运算
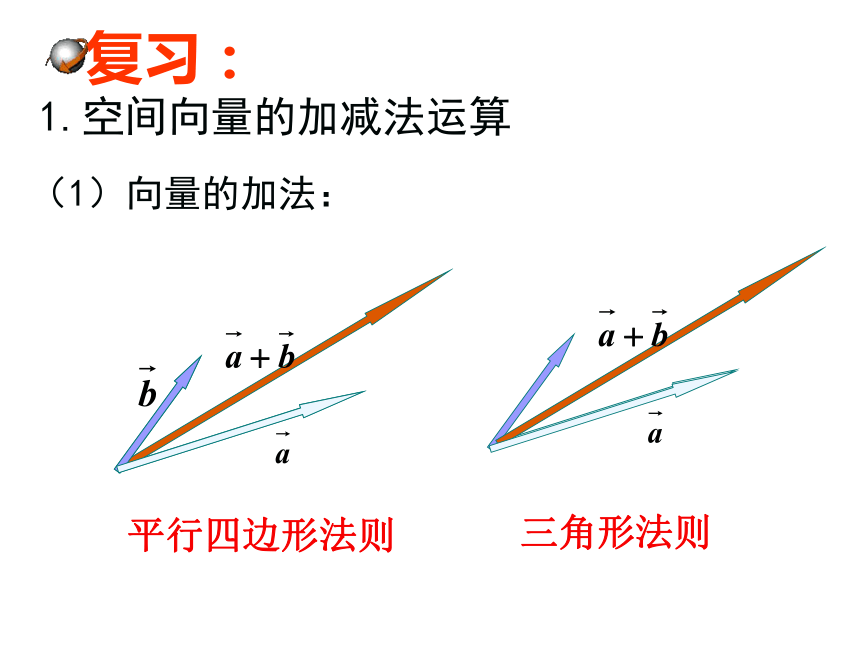
(1)向量的加法:
平行四边形法则
三角形法则
复习:
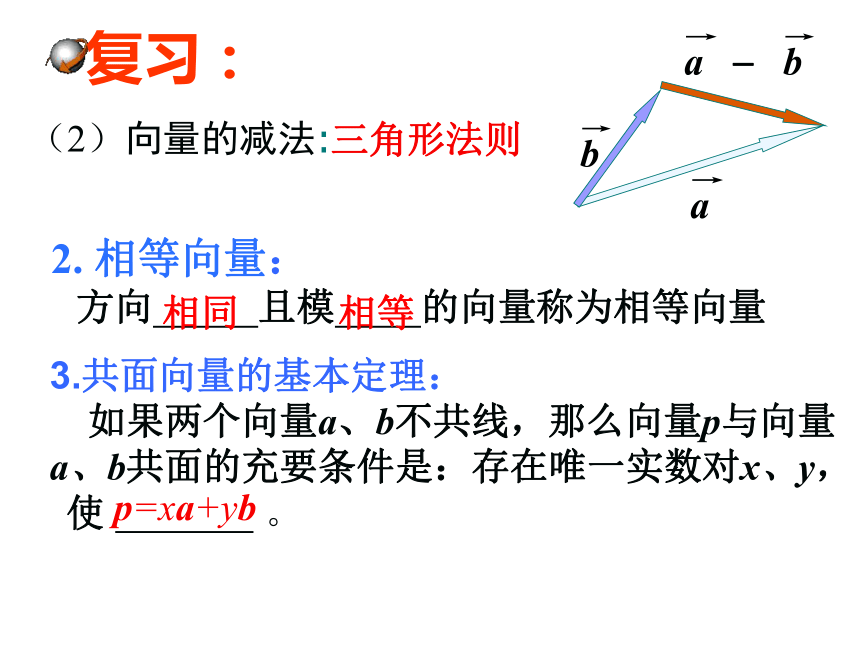
(2)向量的减法
:三角形法则
复习:
2. 相等向量:
方向 且模 的向量称为相等向量
相同
相等
3.共面向量的基本定理:
如果两个向量a、b不共线,那么向量p与向量a、b共面的充要条件是:存在唯一实数对x、y,
使 。
p=xa+yb
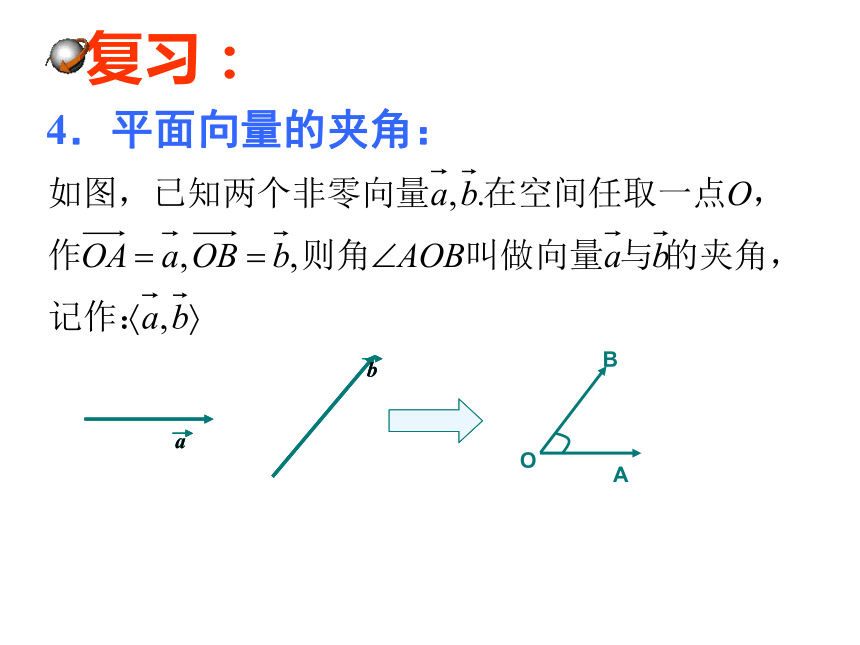
4.平面向量的夹角:
复习:
1) 空间两个向量的夹角的定义
思考:1、〈a,b〉与〈b,a〉相等吗?
2、〈a,b〉与〈a,-b〉相等吗?
注意:〈a,b〉=〈b,a〉,〈a,-b〉=π-〈a,b〉
3.1.3空间向量的数量积运算
2)两个向量的数量积
注:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
3)空间向量的数量积满足的运算律
思考:
4)空间向量的数量积性质:
(求角的依据)
(证明垂直的依据)
(求向量的长度的依据)
1.向量a、b之间的夹角为30°,且|a|=3,
| b |=4,则a·b =__________, a2=__________, (a+2b)·(a-b)=__________.
题型一 利用数量积求夹角
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
【例1】
分析:用向量来证明两直线垂直,只需证明两直线的方向向量的数量积为零即可!
题型二 利用数量积证明垂直关系
【例2】
证明:
为
如图所示,平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,求AC1的长.
题型三 利用数量积求两点间的距离
【例4】
课堂小 结:
空间向量数量积:
可利用数量积解决立体几何中的以下问题:
1、求两直线所成角.
2、证明两直线垂直;
3、求两点之间的距离或线段长度;
作业
P98 A组 3 4 5
B组 1 2
B
课后练习:
3.1.3空间向量的数量积运算
1.空间向量的加减法运算
(1)向量的加法:
平行四边形法则
三角形法则
复习:
(2)向量的减法
:三角形法则
复习:
2. 相等向量:
方向 且模 的向量称为相等向量
相同
相等
3.共面向量的基本定理:
如果两个向量a、b不共线,那么向量p与向量a、b共面的充要条件是:存在唯一实数对x、y,
使 。
p=xa+yb
4.平面向量的夹角:
复习:
1) 空间两个向量的夹角的定义
思考:1、〈a,b〉与〈b,a〉相等吗?
2、〈a,b〉与〈a,-b〉相等吗?
注意:〈a,b〉=〈b,a〉,〈a,-b〉=π-〈a,b〉
3.1.3空间向量的数量积运算
2)两个向量的数量积
注:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
3)空间向量的数量积满足的运算律
思考:
4)空间向量的数量积性质:
(求角的依据)
(证明垂直的依据)
(求向量的长度的依据)
1.向量a、b之间的夹角为30°,且|a|=3,
| b |=4,则a·b =__________, a2=__________, (a+2b)·(a-b)=__________.
题型一 利用数量积求夹角
如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求OA与BC所成角的余弦值.
【例1】
分析:用向量来证明两直线垂直,只需证明两直线的方向向量的数量积为零即可!
题型二 利用数量积证明垂直关系
【例2】
证明:
为
如图所示,平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,∠BAD=90°,∠BAA1=∠DAA1=60°,求AC1的长.
题型三 利用数量积求两点间的距离
【例4】
课堂小 结:
空间向量数量积:
可利用数量积解决立体几何中的以下问题:
1、求两直线所成角.
2、证明两直线垂直;
3、求两点之间的距离或线段长度;
作业
P98 A组 3 4 5
B组 1 2
B
课后练习:
