1.2.1 几个常见函数的导数 课件 19张PPT
文档属性
| 名称 | 1.2.1 几个常见函数的导数 课件 19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 880.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
1.2 导数的计算
1.2.1 几个常用函数的导数
1.导数的定义是什么?
2.导数的几何意义是什么?
函数 y = f (x) =c 的导数
y?=0表示函数y=x图象上每一点处的切线的斜率都为0.
若y=c表示路程关于时间的函数,则y?=0则为某物体的瞬时速度始终为0,即一直处于静止状态.
从几何的角度理解:
从物理的角度理解:
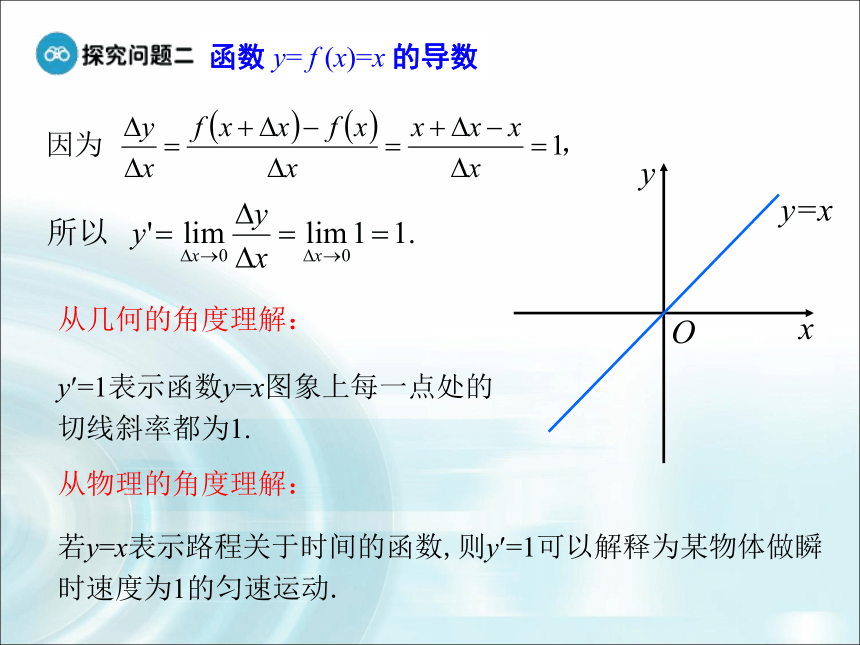
函数 y= f (x)=x 的导数
y?=1表示函数y=x图象上每一点处的切线斜率都为1.
若y=x表示路程关于时间的函数,则y?=1可以解释为某物体做瞬时速度为1的匀速运动.
从几何的角度理解:
从物理的角度理解:
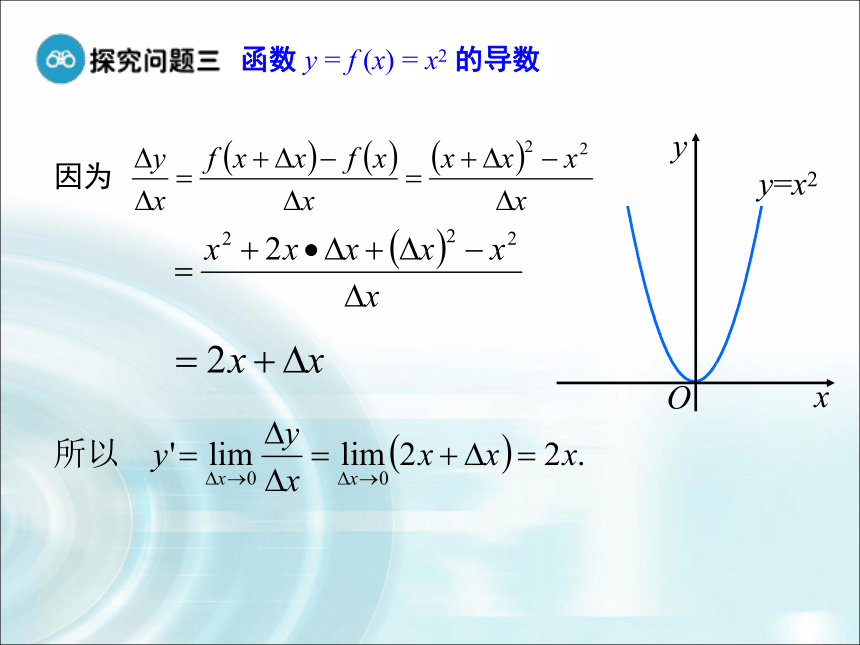
函数 y = f (x) = x2 的导数
y? =2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,
说明随着x的变化,切线的斜率也在变化.
从导数作为函数在一点的瞬时变化率来看,y?=2x表明: 当x<0时,随着x的增加,y=x2减少得越来越慢; 当x>0时,随着x的增加,y=x2增加得越来越快.
从几何的角度理解:
从物理的角度理解:
若y=x2表示路程关于时间的函数,则y?=2x可以解释为某物体作变速运动,它在时刻x的瞬时速度为2x.
探究问题五
例1.在同一平面直角坐标系中,画出函数y=2x,y=3x,y=4x的图象,并根据导数定义,求它们的导数.
(1)从图象上看,它们的导数分别表示什么?
(2)这三个函数中,哪一个增加得最快?哪一个增加得最慢?
(3)函数y=kx(k≠0)增(减)的快慢与什么有关?
问题3:如何求这条切线方程?
本节课我们学习了哪些知识,涉及到哪些数学思想方法?
2.思想:归纳概括思想、类比思想、数形结合的思想.
1.2 导数的计算
1.2.1 几个常用函数的导数
1.导数的定义是什么?
2.导数的几何意义是什么?
函数 y = f (x) =c 的导数
y?=0表示函数y=x图象上每一点处的切线的斜率都为0.
若y=c表示路程关于时间的函数,则y?=0则为某物体的瞬时速度始终为0,即一直处于静止状态.
从几何的角度理解:
从物理的角度理解:
函数 y= f (x)=x 的导数
y?=1表示函数y=x图象上每一点处的切线斜率都为1.
若y=x表示路程关于时间的函数,则y?=1可以解释为某物体做瞬时速度为1的匀速运动.
从几何的角度理解:
从物理的角度理解:
函数 y = f (x) = x2 的导数
y? =2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,
说明随着x的变化,切线的斜率也在变化.
从导数作为函数在一点的瞬时变化率来看,y?=2x表明: 当x<0时,随着x的增加,y=x2减少得越来越慢; 当x>0时,随着x的增加,y=x2增加得越来越快.
从几何的角度理解:
从物理的角度理解:
若y=x2表示路程关于时间的函数,则y?=2x可以解释为某物体作变速运动,它在时刻x的瞬时速度为2x.
探究问题五
例1.在同一平面直角坐标系中,画出函数y=2x,y=3x,y=4x的图象,并根据导数定义,求它们的导数.
(1)从图象上看,它们的导数分别表示什么?
(2)这三个函数中,哪一个增加得最快?哪一个增加得最慢?
(3)函数y=kx(k≠0)增(减)的快慢与什么有关?
问题3:如何求这条切线方程?
本节课我们学习了哪些知识,涉及到哪些数学思想方法?
2.思想:归纳概括思想、类比思想、数形结合的思想.
