1.7.2 定积分在物理中的应用 课件 27张PPT
文档属性
| 名称 | 1.7.2 定积分在物理中的应用 课件 27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 563.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 11:37:32 | ||
图片预览





文档简介
(共27张PPT)
1.7.2 定积分在物理中的应用
1.7 定积分的简单应用:
教学目标:
会用定积分求变速直线运动的路程、变力做功等问题。
教学重难点 :
重点:用定积分求变速直线运动的路程、变力做功等问题的步骤
难点:理解可用定积分求解的物理问题的特点,确定积分的上下限。
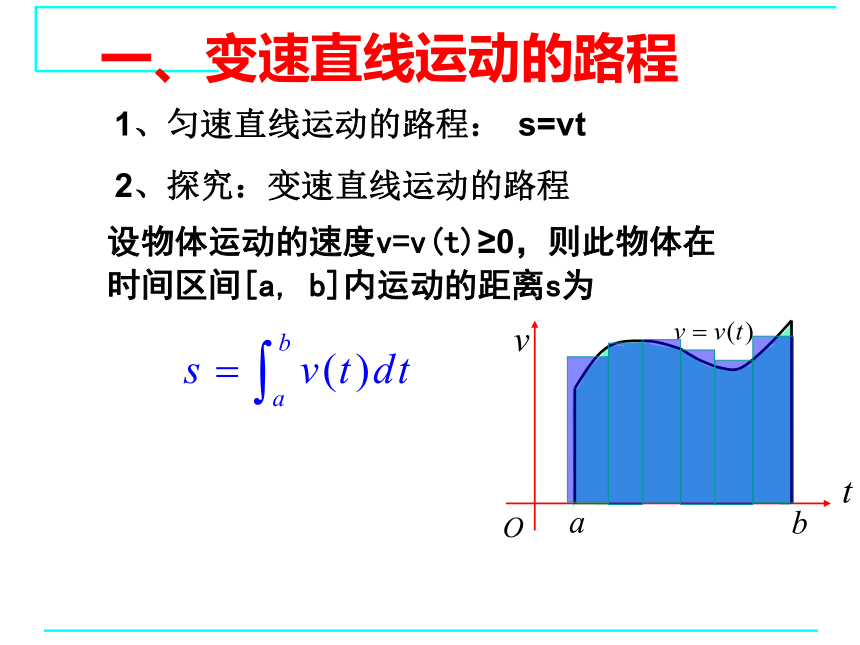
设物体运动的速度v=v(t)≥0,则此物体在
时间区间[a, b]内运动的距离s为
一、变速直线运动的路程
1、匀速直线运动的路程:
2、探究:变速直线运动的路程
s=vt
设物体运动的速度v=v(t)≥0,则此物体在时间区间[a, b]内运动的距离s为
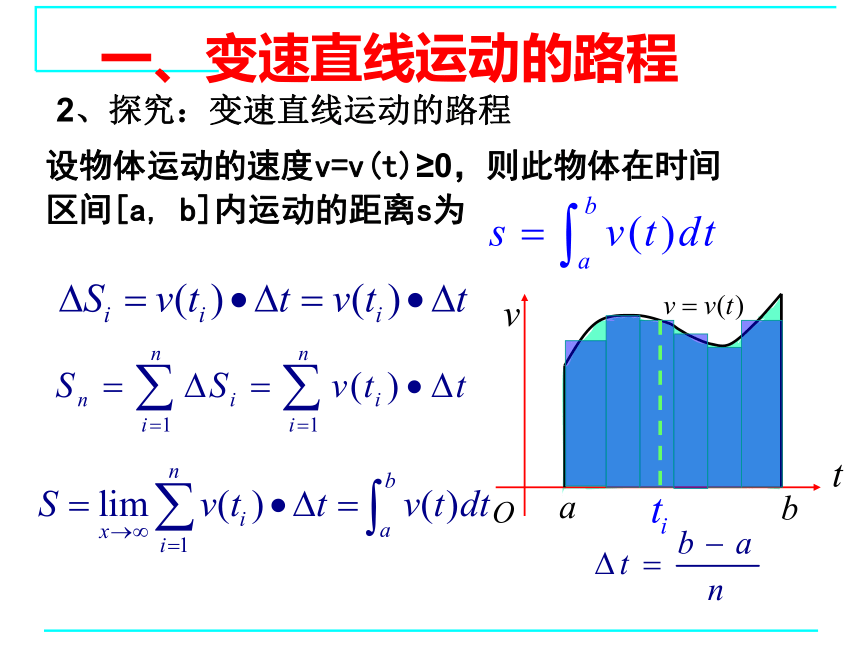
一、变速直线运动的路程
2、探究:变速直线运动的路程
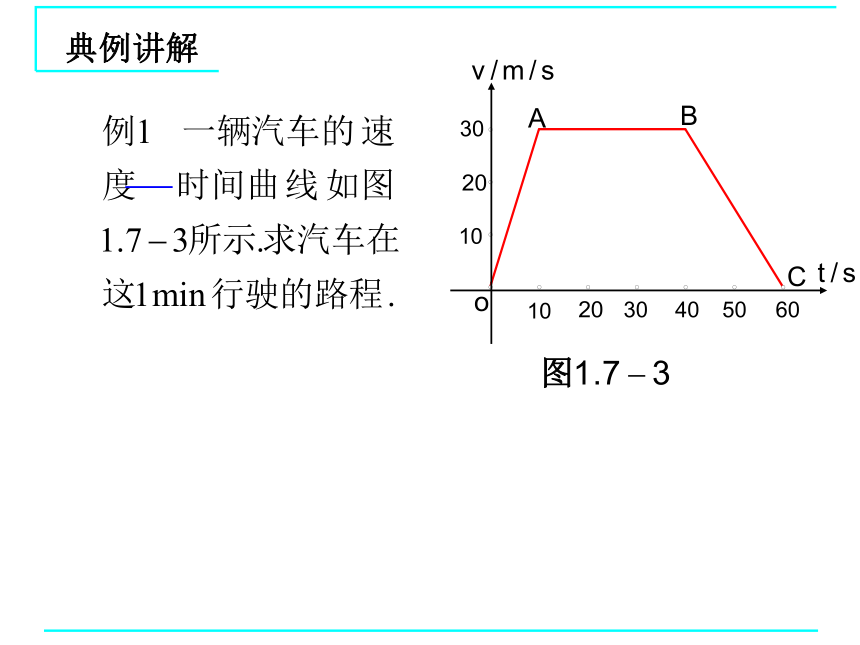
典例讲解
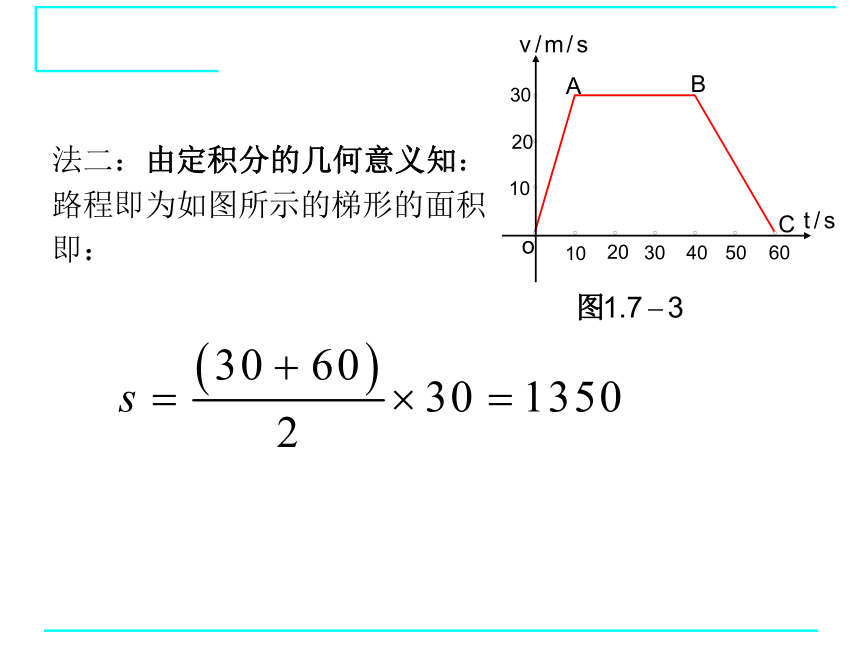
法二:由定积分的几何意义知:
路程即为如图所示的梯形的面积
即:
变速直线运动的物体V(t)区间[a, b]内的积分与位移和路程的关系:
(1)若V(t)≥0,则路程
位移M
(2)若V(t)≤0,则路程
位移M
A、B两站相距7.2km,一辆电车从A站开往B站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,速度为(24-1.2t)m/s,经ts后,在B点恰好停车。
试求:(1)A、C间的距离;
(2)B、D间的距离;
(3)电车从A站到B站所需的时间。
巩固练习
A
B
C
D
变速
Vc=24
匀速
变速
VB=0
VD=24
V=1.2t
V=24-1.2t
(1)设A到C的时间为t1则1.2t=24, t1=20(s),
则AC=
(2)设D到B的时间为t2则24-1.2t2=0, t2=20(s),
则DB=
A
B
C
D
变速
Vc=24
匀速
变速
VB=0
VD=24
V=1.2t
V=24-1.2t
(3)CD=7200-480=6720(m),易知从C到D的时间为280(s)
所求时间为20+280+20=320(s)
二、变力沿直线做功
变力沿直线所做的功
物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a移动到x=b(a
变力沿直线所做的功
物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a移动到x=b(a
典例讲解
如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功( )
A. 0.18J B. 0.26J C. 0.12J D. 0.28J
所以做功就是求定积分
则由题可得
解:设
A
巩固练习:
例3 一个带+q电量的点电荷放在r轴上坐标原点处,形成一个电场,已知该电场中,距离坐标原点为r处的单位电荷受到的电场力由公式: 确定,在该电场中,一个单位正电荷在电场力作用下,沿着r轴方向从r=a到r=b(a
变式训练
解:
由题意,所求功为
设物体运动的速度v=v(t) (v(t)≥0) ,则此物体在时间区间[a, b]内运动的路程s为
1、变速直线运动的路程
2、变力沿直线所作的功
物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a点移动到x= b点,则变力F(x) 所做的功为:
小结
发射火箭需要计算克服地球引力所作的功。设火箭的质量为 m 。
(1)将火箭垂直地向上发射到离地面高H 时,需作多少功?
(2)并由此计算初速度至少为多少时,方可使火箭脱离地球的引力范围?
课外拓展:探索宇宙
发射火箭需要计算克服地球引力所作的功。设火箭的质量为 m 。
课外拓展:探索宇宙
x
o
R
R+H
火箭所受地球的引力
当火箭在地面上(x=R)时,火箭所受的引力就是火箭的重力mg
(1)将火箭垂直地向上发射到离地面高H 时,需作多少功?
解
取 ox 轴竖直向上
x
o
R
R+H
地球半径设为R,质量为M,由万有引力定律,火箭所受地球的引力
f随高度 x 而变化
当火箭在地面上,火箭所受的引力就是火箭的重力mg,即 x =R 时
克服地球引力的外力F与 f 大小相等为了发射火箭,必须克服地球引力
所须作的功
为了使火箭脱离地球引力范围,即要把火箭发射到无穷远处
则动能为
因此要使火箭脱离地球引力范围,须有
代入上式得
—第二宇宙速度
这功是由火箭上的动能转化而来,若火箭离开地面时的初速度为
(2)并由此计算初速度至少为多少时,方可使火箭脱离地球的引力范围?
课后作业
1.课本59页练习1,2
2.课本60页习题A组4,5
1.7.2 定积分在物理中的应用
1.7 定积分的简单应用:
教学目标:
会用定积分求变速直线运动的路程、变力做功等问题。
教学重难点 :
重点:用定积分求变速直线运动的路程、变力做功等问题的步骤
难点:理解可用定积分求解的物理问题的特点,确定积分的上下限。
设物体运动的速度v=v(t)≥0,则此物体在
时间区间[a, b]内运动的距离s为
一、变速直线运动的路程
1、匀速直线运动的路程:
2、探究:变速直线运动的路程
s=vt
设物体运动的速度v=v(t)≥0,则此物体在时间区间[a, b]内运动的距离s为
一、变速直线运动的路程
2、探究:变速直线运动的路程
典例讲解
法二:由定积分的几何意义知:
路程即为如图所示的梯形的面积
即:
变速直线运动的物体V(t)区间[a, b]内的积分与位移和路程的关系:
(1)若V(t)≥0,则路程
位移M
(2)若V(t)≤0,则路程
位移M
A、B两站相距7.2km,一辆电车从A站开往B站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,速度为(24-1.2t)m/s,经ts后,在B点恰好停车。
试求:(1)A、C间的距离;
(2)B、D间的距离;
(3)电车从A站到B站所需的时间。
巩固练习
A
B
C
D
变速
Vc=24
匀速
变速
VB=0
VD=24
V=1.2t
V=24-1.2t
(1)设A到C的时间为t1则1.2t=24, t1=20(s),
则AC=
(2)设D到B的时间为t2则24-1.2t2=0, t2=20(s),
则DB=
A
B
C
D
变速
Vc=24
匀速
变速
VB=0
VD=24
V=1.2t
V=24-1.2t
(3)CD=7200-480=6720(m),易知从C到D的时间为280(s)
所求时间为20+280+20=320(s)
二、变力沿直线做功
变力沿直线所做的功
物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a移动到x=b(a
变力沿直线所做的功
物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a移动到x=b(a
典例讲解
如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功( )
A. 0.18J B. 0.26J C. 0.12J D. 0.28J
所以做功就是求定积分
则由题可得
解:设
A
巩固练习:
例3 一个带+q电量的点电荷放在r轴上坐标原点处,形成一个电场,已知该电场中,距离坐标原点为r处的单位电荷受到的电场力由公式: 确定,在该电场中,一个单位正电荷在电场力作用下,沿着r轴方向从r=a到r=b(a
变式训练
解:
由题意,所求功为
设物体运动的速度v=v(t) (v(t)≥0) ,则此物体在时间区间[a, b]内运动的路程s为
1、变速直线运动的路程
2、变力沿直线所作的功
物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a点移动到x= b点,则变力F(x) 所做的功为:
小结
发射火箭需要计算克服地球引力所作的功。设火箭的质量为 m 。
(1)将火箭垂直地向上发射到离地面高H 时,需作多少功?
(2)并由此计算初速度至少为多少时,方可使火箭脱离地球的引力范围?
课外拓展:探索宇宙
发射火箭需要计算克服地球引力所作的功。设火箭的质量为 m 。
课外拓展:探索宇宙
x
o
R
R+H
火箭所受地球的引力
当火箭在地面上(x=R)时,火箭所受的引力就是火箭的重力mg
(1)将火箭垂直地向上发射到离地面高H 时,需作多少功?
解
取 ox 轴竖直向上
x
o
R
R+H
地球半径设为R,质量为M,由万有引力定律,火箭所受地球的引力
f随高度 x 而变化
当火箭在地面上,火箭所受的引力就是火箭的重力mg,即 x =R 时
克服地球引力的外力F与 f 大小相等为了发射火箭,必须克服地球引力
所须作的功
为了使火箭脱离地球引力范围,即要把火箭发射到无穷远处
则动能为
因此要使火箭脱离地球引力范围,须有
代入上式得
—第二宇宙速度
这功是由火箭上的动能转化而来,若火箭离开地面时的初速度为
(2)并由此计算初速度至少为多少时,方可使火箭脱离地球的引力范围?
课后作业
1.课本59页练习1,2
2.课本60页习题A组4,5
