阅读与思考 平面与空间中的余弦定理 课件 30张PPT
文档属性
| 名称 | 阅读与思考 平面与空间中的余弦定理 课件 30张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
人教A版高二数学选修2-2第二章《阅读与思考》
古人由带齿的草叶和蝗虫的齿牙发明了锯,现代的科学家仿照鱼的外形和它们在水中的沉浮原理发明了潜水艇。这些发明作用了我们数学中的重要数学思想是什么呢?
一、课堂引入
类比推理
“即使在数学里,发现真理的主要工具也是归纳和类比”
—法国数学家拉普拉斯
一、课堂引入
“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密.” —开普勒
波利亚(George Polya,1887-1985),美籍匈牙利数学家,著名的数学教育家,享有国际盛誉的数学方法论大师。他一生发表了200多篇论文和许多专著,著有《怎样解题》、《数学的发现》、《数学与猜想》等。在数学教育领域最突出的贡献是开辟了数学启发法研究的新领域,为数学方法论研究的现代复兴奠定了必要的理论基础。
一、课堂引入
一、复习旧知
类比推理的定义:
类比推理的定义:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理,类比推理属于合情推理。
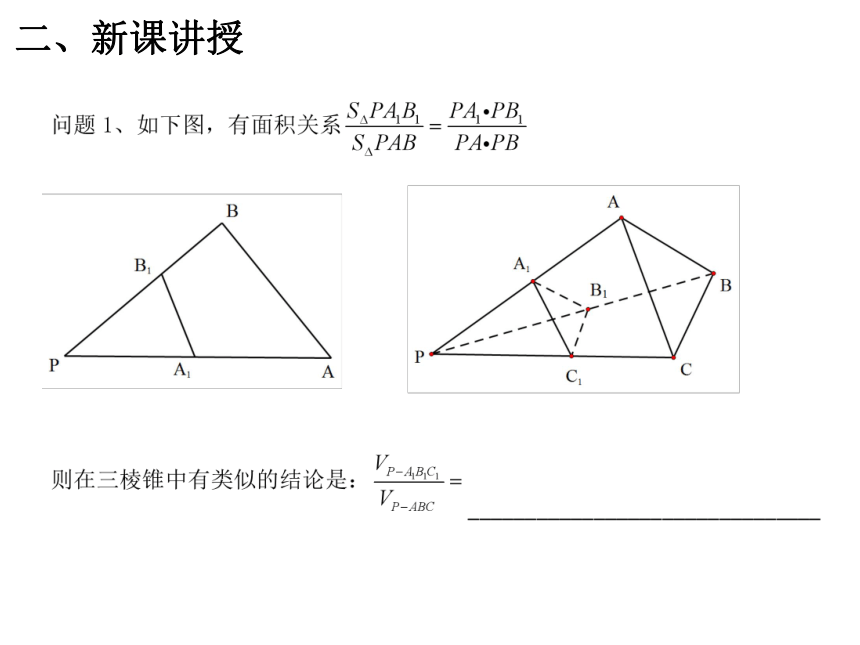
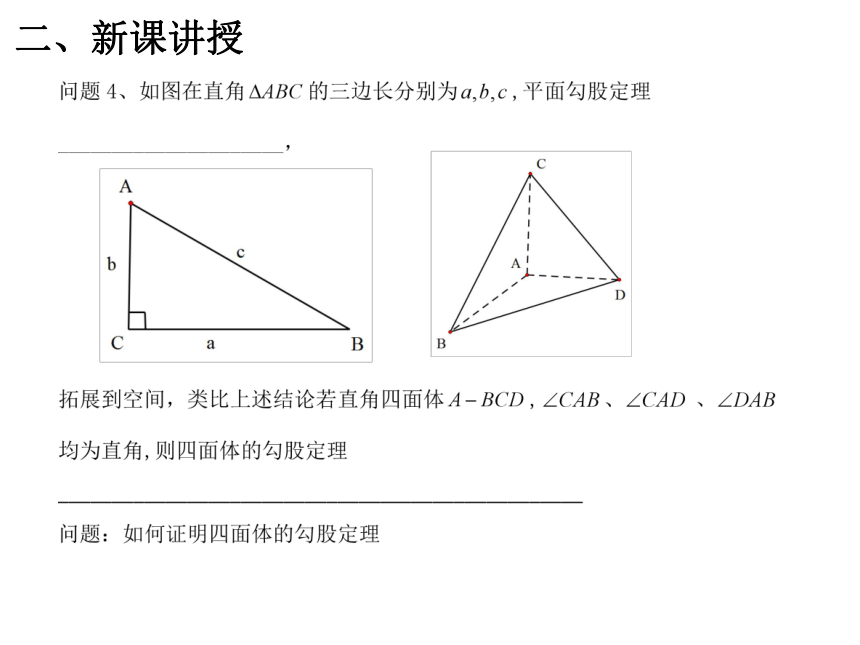
二、新课讲授
二、新课讲授
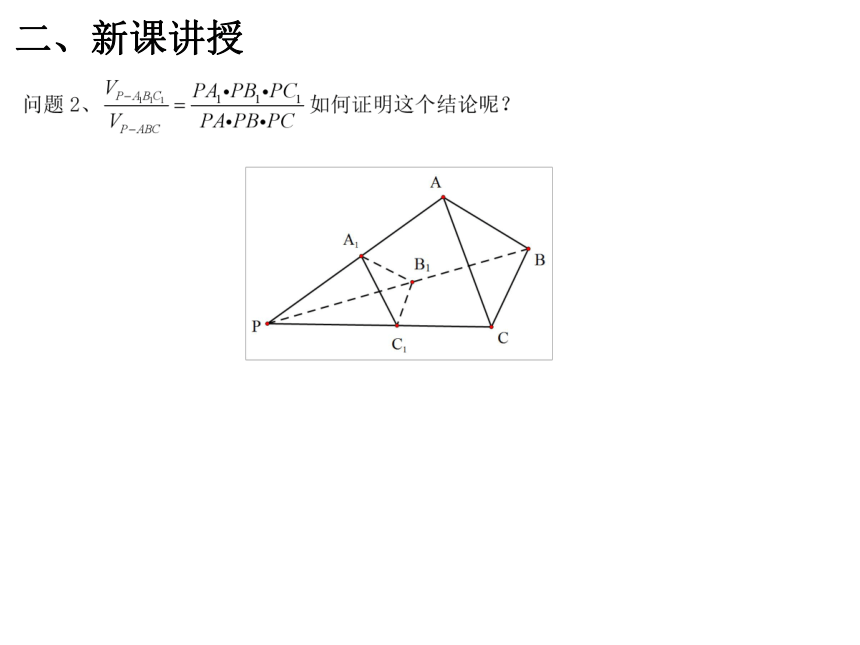
二、新课讲授
二、新课讲授
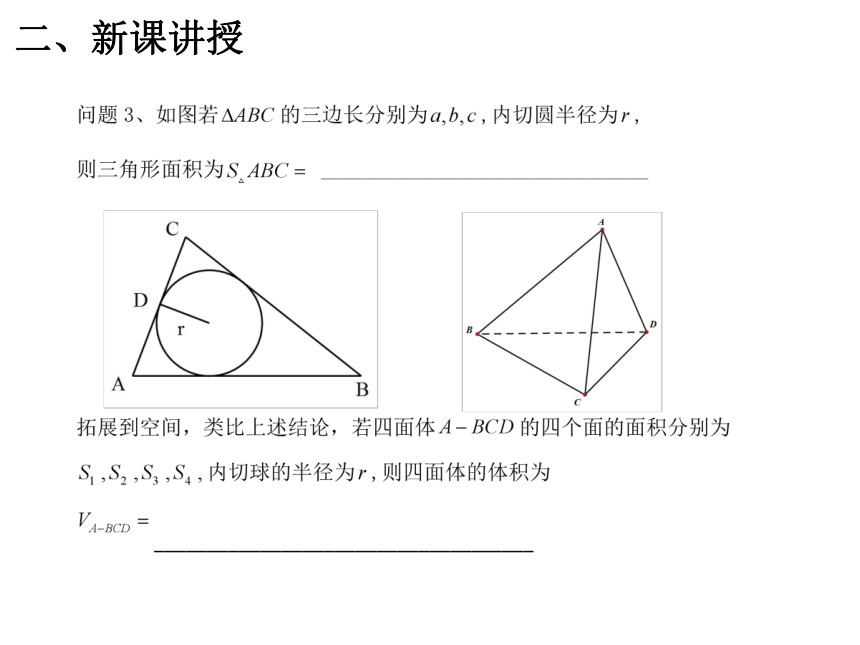
二、新课讲授
二、新课讲授
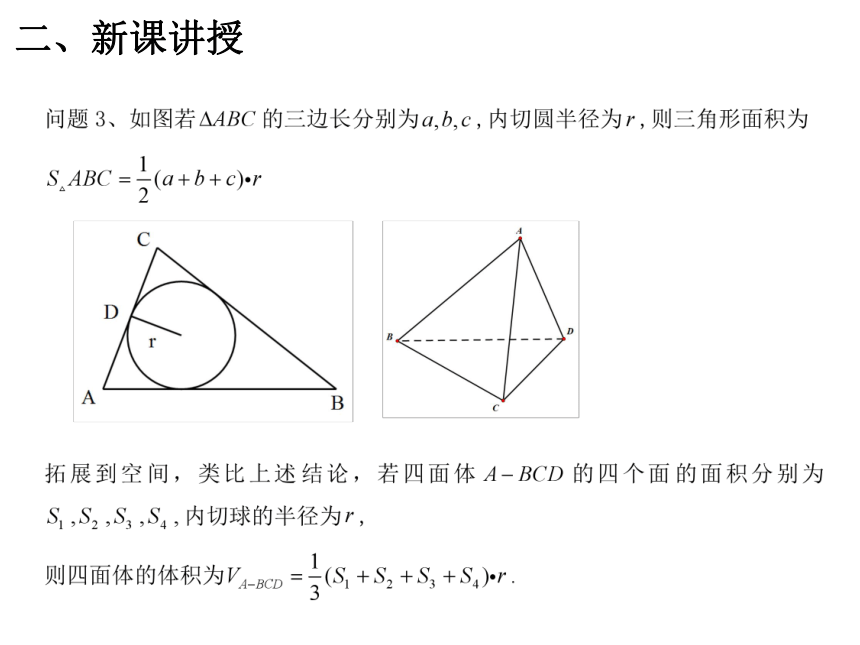
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
延时符
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
延时符
二、新课讲授
延时符
二、新课讲授
___________
___________
___________
②③④代入⑤得
证明:
二、新课讲授
本节课由平面余弦定理类比得到了空间余弦定理,空间余弦定理揭示了四面体各面面积与夹角间的内在联系,形式上与平面余弦定理极为相似,仅仅是量纲和维数的差异。我们从平面几何出发,运用类比推理的形式,通过猜想发现立体几何中存在的类似结论,所以平面几何与立体几何之间有着千丝万缕的联系.
三、课堂小结
人教A版高二数学选修2-2第二章《阅读与思考》
古人由带齿的草叶和蝗虫的齿牙发明了锯,现代的科学家仿照鱼的外形和它们在水中的沉浮原理发明了潜水艇。这些发明作用了我们数学中的重要数学思想是什么呢?
一、课堂引入
类比推理
“即使在数学里,发现真理的主要工具也是归纳和类比”
—法国数学家拉普拉斯
一、课堂引入
“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密.” —开普勒
波利亚(George Polya,1887-1985),美籍匈牙利数学家,著名的数学教育家,享有国际盛誉的数学方法论大师。他一生发表了200多篇论文和许多专著,著有《怎样解题》、《数学的发现》、《数学与猜想》等。在数学教育领域最突出的贡献是开辟了数学启发法研究的新领域,为数学方法论研究的现代复兴奠定了必要的理论基础。
一、课堂引入
一、复习旧知
类比推理的定义:
类比推理的定义:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理,类比推理属于合情推理。
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
延时符
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
二、新课讲授
延时符
二、新课讲授
延时符
二、新课讲授
___________
___________
___________
②③④代入⑤得
证明:
二、新课讲授
本节课由平面余弦定理类比得到了空间余弦定理,空间余弦定理揭示了四面体各面面积与夹角间的内在联系,形式上与平面余弦定理极为相似,仅仅是量纲和维数的差异。我们从平面几何出发,运用类比推理的形式,通过猜想发现立体几何中存在的类似结论,所以平面几何与立体几何之间有着千丝万缕的联系.
三、课堂小结
