阅读与思考 平面与空间中的余弦定理 课件 38张PPT
文档属性
| 名称 | 阅读与思考 平面与空间中的余弦定理 课件 38张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
阅读与思考
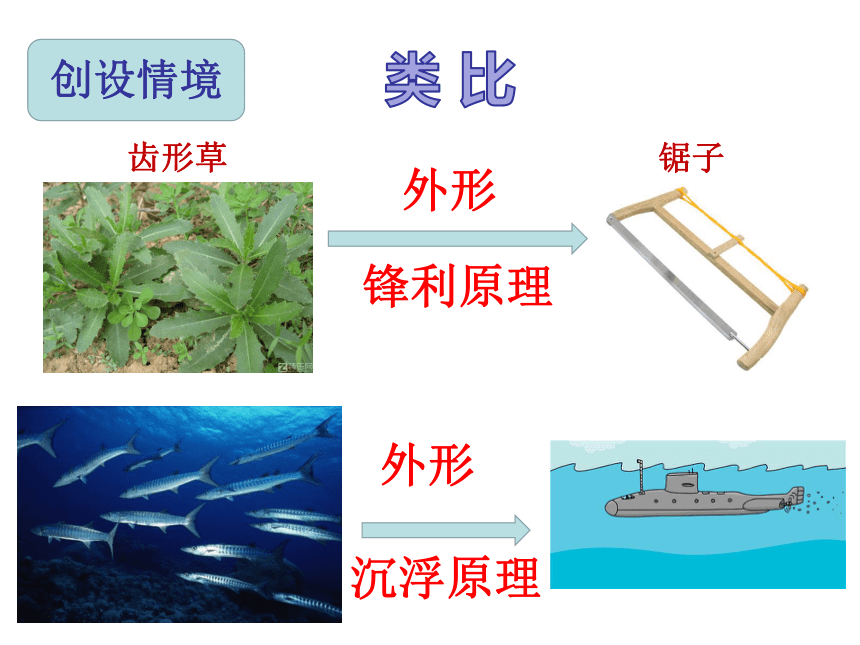
外形
锋利原理
齿形草
锯子
外形
沉浮原理
创设情境
由其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理。
复习回顾
类比推理的特点:
由特殊到特殊的推理;具有探索、发现的功能;
结论不一定正确。
从具体问题
出发
观察、分析、
比较、联想
猜想
类比
证明
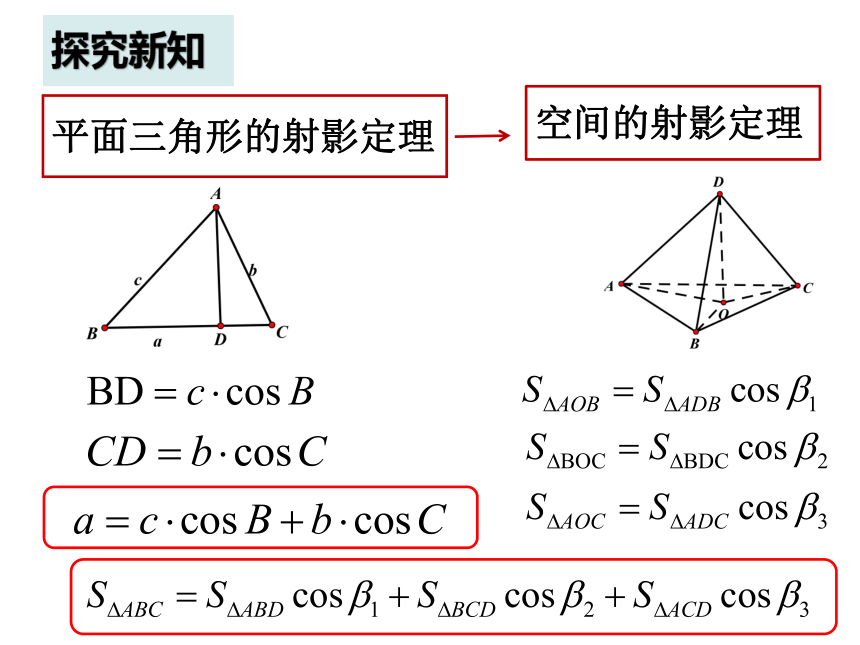
平面三角形的射影定理
空间的射影定理
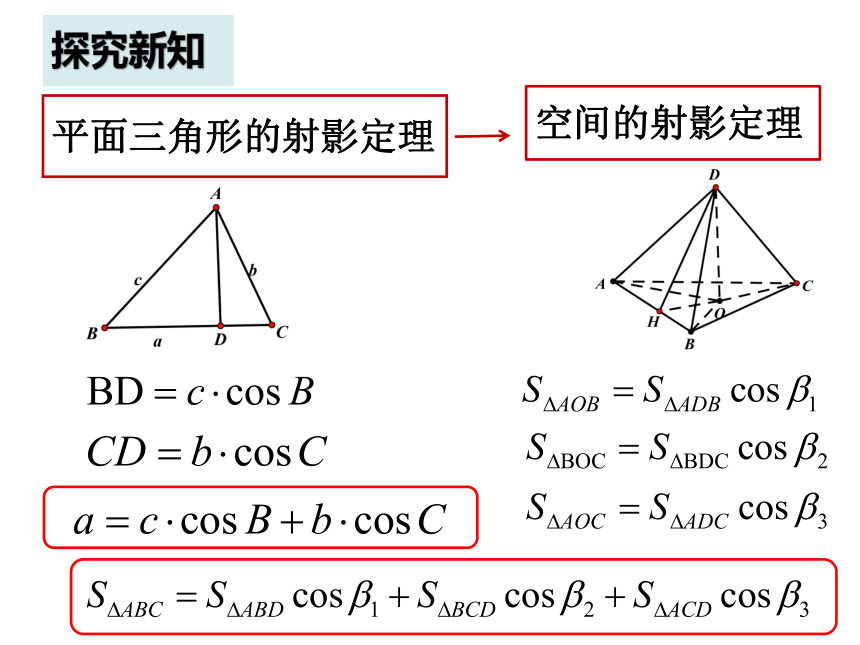
探究新知
平面三角形的射影定理
空间的射影定理
探究新知
一边
探究新知
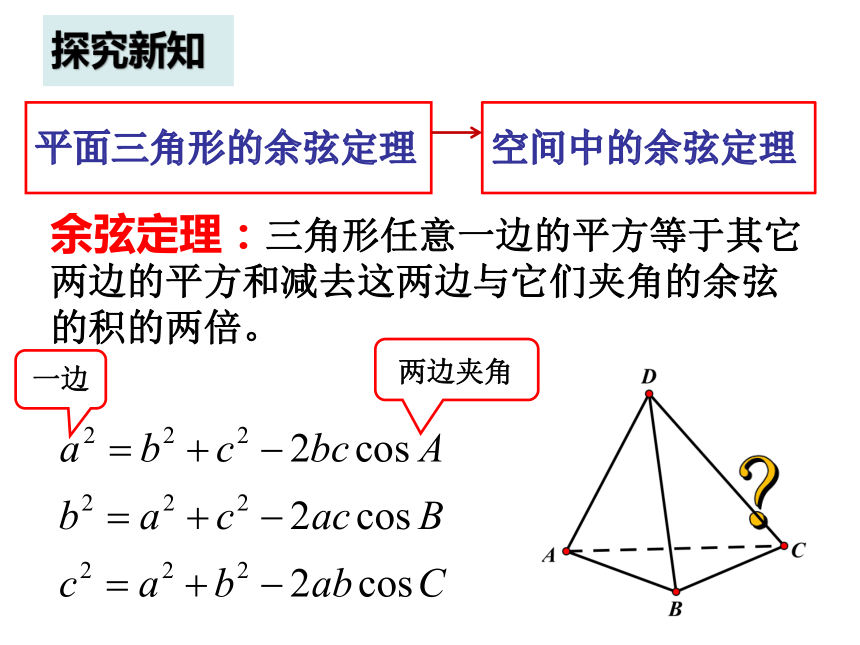
余弦定理:三角形任意一边的平方等于其它 两边的平方和减去这两边与它们夹角的余弦的积的两倍。
把??代入上式,得
由射影定理知:
化简可得:
巩固训练:
直角三角形勾股定理
引申拓展
已知三角形ABC内切圆半径为R,
则三角形的面积
若四面体ABCD的内切球半径为R,则四面体的体积等于
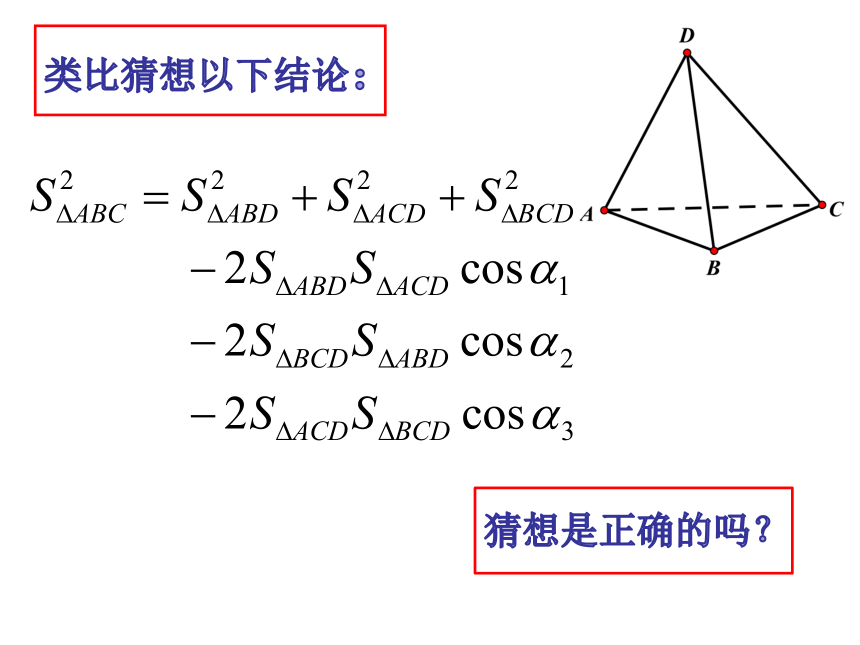
类比到空间会有什么结论?
小试牛刀
今天你学了什么?
从具体问题
出发
观察、分析、
比较、联想
猜想
类比
证明
今天你学了什么?
我们知道:
三角形ABC的内切圆
四面体的内切球R=??
三角形的特征 四面体的特征
三边a,b,c
三内角A,B,C
三角形的性质
四面体的性质
三角形的两边之和大于第三边 四面体的任意三个面面积之和大于第四个面面积
三角形的内角平分线交于一点,且这个点是三角形的内切圆圆心
四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心
(1)圆有切线,切线与圆只交于一点,切点到圆心的距离等于圆的半径;
(2)平面内不共线的3个点确定一个圆。
(1)球存在这样的平面,与球只交于一点,该点到球心的距离等于球大的半径;
(2)空间中不共面的4个点确定一个球。
圆的周长 球的表面积
圆的面积 球的体积
以点P(a,b)为圆心,r为半径的圆方程为
以点P(a,b,c)为球心,r为半径的球方程为
我国古代工匠鲁班类比带齿的草叶和蝗虫的齿牙,发明了锯;
人们仿照鱼类的外形和它们在水中的沉浮原理,发明了潜水艇;
为了回答“火星上是否由生命”这个问题,科学家们把火星与地球作类比,发现火星具有一些与地球类似的特征,如火星也是围绕太阳运行、绕轴自传的行星,也有大气层,在一年中也有季节的变更,而且火星上大部分时间的温度适合地球上某些已知生物的生存,等等。因此,科学家猜想:火星上也可能由生命存在。
余弦定理:三角形任意一边的平方等于其它 两边的平方和减去这两边与它们夹角的余弦的积的两倍。
一边
猜想:
火星可能有
生命存在
围绕太阳运行、绕轴自传的行星,
也有大气层,有季节的变更,
而且火星上大部分时间的温度
适合地球上某些已知生物的生存
相同特征
直角三角形
两条边互相垂直 三个面两两垂直
勾股定理
平面三角形的射影定理
空间的射影定理
平面三角形的射影定理
空间的射影定理
外形
锋利原理
我国古代工匠鲁班类比带齿的草叶,
发明了锯;
齿形草
锯子
引入
外形
沉浮原理
人们仿照鱼类的外形和它们在水中的
沉浮原理,发明了潜水艇;
引入
由其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理。
类比推理的步骤:
从具体问题
出发
观察、分析、
比较、联想
猜想
类比
复习回顾
类比推理的特点:
由特殊到特殊的推理;具有探索、发现的功能;
结论不一定正确。
已知三角形的特征 类比四面体的特征
三边a,b,c
三内角A,B,C
波利亚(George Polya1887-1985),美籍匈牙利数学家,
著名的数学教育家,享有国际盛誉的数学方法论大师。
他一生发表了200多篇论文和许多专著,著有《怎样解题》、
《数学的发现》、《数学与猜想》等。
在数学教育领域最突出的贡献是开辟了数学启发法研究的新领域,为数学方法论研究的现代复兴奠定了必要的理论基础。
阅读与思考
外形
锋利原理
齿形草
锯子
外形
沉浮原理
创设情境
由其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理。
复习回顾
类比推理的特点:
由特殊到特殊的推理;具有探索、发现的功能;
结论不一定正确。
从具体问题
出发
观察、分析、
比较、联想
猜想
类比
证明
平面三角形的射影定理
空间的射影定理
探究新知
平面三角形的射影定理
空间的射影定理
探究新知
一边
探究新知
余弦定理:三角形任意一边的平方等于其它 两边的平方和减去这两边与它们夹角的余弦的积的两倍。
把??代入上式,得
由射影定理知:
化简可得:
巩固训练:
直角三角形勾股定理
引申拓展
已知三角形ABC内切圆半径为R,
则三角形的面积
若四面体ABCD的内切球半径为R,则四面体的体积等于
类比到空间会有什么结论?
小试牛刀
今天你学了什么?
从具体问题
出发
观察、分析、
比较、联想
猜想
类比
证明
今天你学了什么?
我们知道:
三角形ABC的内切圆
四面体的内切球R=??
三角形的特征 四面体的特征
三边a,b,c
三内角A,B,C
三角形的性质
四面体的性质
三角形的两边之和大于第三边 四面体的任意三个面面积之和大于第四个面面积
三角形的内角平分线交于一点,且这个点是三角形的内切圆圆心
四面体的六个二面角的平分面交于一点,且这个点是四面体内切球的球心
(1)圆有切线,切线与圆只交于一点,切点到圆心的距离等于圆的半径;
(2)平面内不共线的3个点确定一个圆。
(1)球存在这样的平面,与球只交于一点,该点到球心的距离等于球大的半径;
(2)空间中不共面的4个点确定一个球。
圆的周长 球的表面积
圆的面积 球的体积
以点P(a,b)为圆心,r为半径的圆方程为
以点P(a,b,c)为球心,r为半径的球方程为
我国古代工匠鲁班类比带齿的草叶和蝗虫的齿牙,发明了锯;
人们仿照鱼类的外形和它们在水中的沉浮原理,发明了潜水艇;
为了回答“火星上是否由生命”这个问题,科学家们把火星与地球作类比,发现火星具有一些与地球类似的特征,如火星也是围绕太阳运行、绕轴自传的行星,也有大气层,在一年中也有季节的变更,而且火星上大部分时间的温度适合地球上某些已知生物的生存,等等。因此,科学家猜想:火星上也可能由生命存在。
余弦定理:三角形任意一边的平方等于其它 两边的平方和减去这两边与它们夹角的余弦的积的两倍。
一边
猜想:
火星可能有
生命存在
围绕太阳运行、绕轴自传的行星,
也有大气层,有季节的变更,
而且火星上大部分时间的温度
适合地球上某些已知生物的生存
相同特征
直角三角形
两条边互相垂直 三个面两两垂直
勾股定理
平面三角形的射影定理
空间的射影定理
平面三角形的射影定理
空间的射影定理
外形
锋利原理
我国古代工匠鲁班类比带齿的草叶,
发明了锯;
齿形草
锯子
引入
外形
沉浮原理
人们仿照鱼类的外形和它们在水中的
沉浮原理,发明了潜水艇;
引入
由其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理。
类比推理的步骤:
从具体问题
出发
观察、分析、
比较、联想
猜想
类比
复习回顾
类比推理的特点:
由特殊到特殊的推理;具有探索、发现的功能;
结论不一定正确。
已知三角形的特征 类比四面体的特征
三边a,b,c
三内角A,B,C
波利亚(George Polya1887-1985),美籍匈牙利数学家,
著名的数学教育家,享有国际盛誉的数学方法论大师。
他一生发表了200多篇论文和许多专著,著有《怎样解题》、
《数学的发现》、《数学与猜想》等。
在数学教育领域最突出的贡献是开辟了数学启发法研究的新领域,为数学方法论研究的现代复兴奠定了必要的理论基础。
