2020年六年级下册数学总复习课件-第21课时 找规律 人教版(共23张PPT)
文档属性
| 名称 | 2020年六年级下册数学总复习课件-第21课时 找规律 人教版(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 679.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 15:02:36 | ||
图片预览







文档简介
(共23张PPT)
专题十 数学思考
第21课时 找规律
考点一 数列的规律
例1 (2019?抚顺)找规律填空:0、1、1、2、3、5、8、13、( )、( )……
解析:这类题目一般先要找出排列的规律,并按规律继续写出几个数,或将中间缺少的数填起来。解答时,需要较强的数感,一般情况下有相邻两个数的和(或差、商)相等或呈现一定的规律,不同数位上的数字按一定的规律排列等。而本题中的数在逐渐变大,但又不是简单地做加上一个固定数的加法,或是所加数在递增的加法。从最前面开始,0+1=1,1+1=2,再接着有1+2=3,2+3=5,3+5=8,5+8=13,8+13=21,13+21=34……
答案:21 34
[小试身手]
(2019?兴化)按规律填数:
(1) 8、11、14、17、( )、23……
(2) 一列数1、2、2、3、3、3、4、4、4、4……中的第35个数是( )。
(2019?泰兴)有一列数:、、、……则第6个数是( ),第n个数是( )。
(2018?四川)先找规律,再填数。
+ -1= , + - , + - = , + - = …则
+ - ( )=
20
8
考点二 图形变化的规律
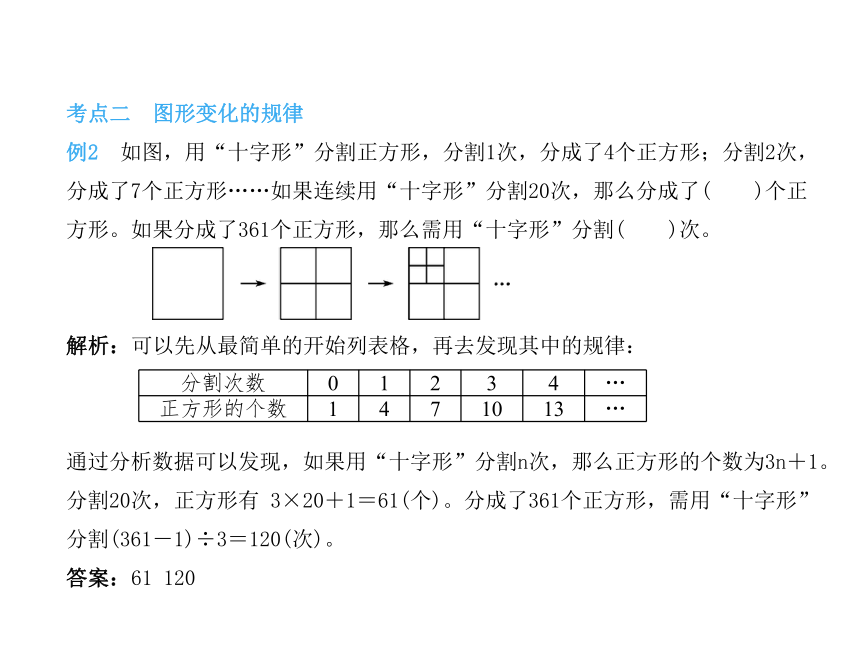
例2 如图,用“十字形”分割正方形,分割1次,分成了4个正方形;分割2次,分成了7个正方形……如果连续用“十字形”分割20次,那么分成了( )个正方形。如果分成了361个正方形,那么需用“十字形”分割( )次。
解析:可以先从最简单的开始列表格,再去发现其中的规律:
通过分析数据可以发现,如果用“十字形”分割n次,那么正方形的个数为3n+1。分割20次,正方形有 3×20+1=61(个)。分成了361个正方形,需用“十字形”分割(361-1)÷3=120(次)。
答案:61 120
分割次数 0 1 2 3 4 …
正方形的个数 1 4 7 10 13 …
[小试身手]
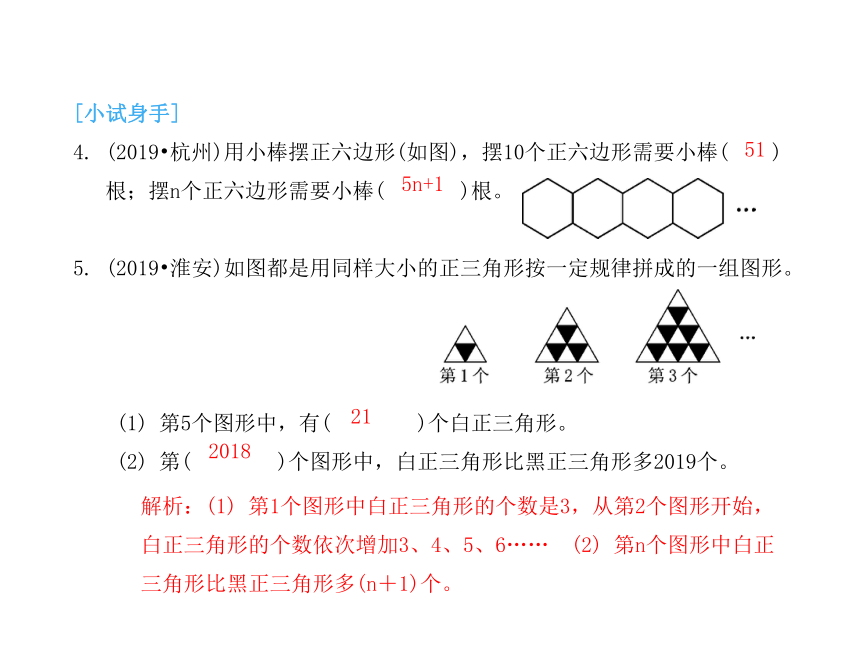
(2019?杭州)用小棒摆正六边形(如图),摆10个正六边形需要小棒( )根;摆n个正六边形需要小棒( )根。
(2019?淮安)如图都是用同样大小的正三角形按一定规律拼成的一组图形。
(1) 第5个图形中,有( )个白正三角形。
(2) 第( )个图形中,白正三角形比黑正三角形多2019个。
51
5n+1
21
2018
解析:(1) 第1个图形中白正三角形的个数是3,从第2个图形开始,白正三角形的个数依次增加3、4、5、6…… (2) 第n个图形中白正三角形比黑正三角形多(n+1)个。
6. 在下面的方格图中画一条直线,最多能穿过几个方格?
穿过1×1的方格图,最多可穿过( )个方格。
穿过2×2的方格图,最多可穿过( )个方格。
穿过10×10的方格图,最多可穿过( )个方格。
1
3
19
考点三 间隔现象的规律
例3 (2019?武汉)300米长的道路两旁,均每隔30米种1棵树(端点处都种),一共种了多少棵树?每两棵树之间放3张躺椅,一共有多少张躺椅?
解析:根据题意,端点处都种也就是两端都种树,所以树的棵数=间隔数+1。300÷30=10(个)间隔,就有10+1=11(棵)树。然后还有一个关键条件需要注意,路的两旁都种树,所以共有11×2=22(棵)树。每两棵树之间有3张躺椅,即有10×2×3=60(张)躺椅。
答案:300÷30=10(个)
10+1=11(棵)
11×2=22(棵)
10×3×2=60(张)
答:一共种了22棵树,一共有60张躺椅。
运用分类讨论法解题
间隔现象的规律在实际生活中很常见,本题需注意分类讨论,在不封闭图形中,有三种情况:(1) 两端都栽,植树的棵数=间隔数+1;(2) 两端都不栽,植树的棵数=间隔数-1;(3) 一端栽,一端不栽,植树的棵数=间隔数。
[小试身手]
(1) 一条从南往北的河的一边栽了75棵柳树(两端都栽),每两棵柳树之间栽了1棵杨树,杨树栽了( )棵。
(2) 沿圆形池塘的一周栽了75棵柳树,每两棵柳树之间栽了1棵杨树,杨树栽了( )棵。
学校的圆形花坛的周长为32米,每隔 4米放一盆花,共放( )盆花。
A. 7 B. 8 C. 9
(2018?大理)20面小旗插在迎宾道的两旁(两端都插),每相邻两面小旗的距离是10米,这条迎宾道长多少米?
74
75
20÷2=10(面) 10-1=9(个) 10×9=90(米)
B
考点四 搭配的规律
例4 (2019?商丘)从6名候选人中选出2人参加演讲比赛,共有( )种选法。
A. 10 B. 12 C. 15 D. 18
解析:本题要有序思考,不妨将6人依次编号为1、2、3、4、5、6,然后从1开始去选人搭配,1与2、1与3、1与4、1与5、1与6,共5种选法,接着从2去选人搭配,2与3、2与4、2与5、2与6,共4种选法,依此类推,共有3种、2种和1种选法,这样一共有5+4+3+2+1=15(种)。这道题还可以这样想,1人出来选人搭配,共有5种选法,这样6人就有6个5种选法,然后因为重复,再除以2即可。
答案:C
[小试身手]
(2019?广元)学校为艺术节选送节目,要从2个合唱节目中选1个,3个舞蹈节目中选1个,一共有( )种不同的选送方案。
(2019?太仓)有4支足球队进行踢足球比赛,每两支队都要赛一场,一共要赛( )场。有4个小朋友每两人互寄一张贺卡,一共要准备( )张贺卡。
甲、乙、丙、丁四位同学进行乒乓球比赛,每两位同学之间都要比一场,一共要比( )场。如果甲的成绩是两胜一负,乙的成绩是三战全胜,丙的成绩是三战皆负,那么丁的成绩是( )。
6
6
一胜两负
12
6
考点五 周期的规律
例5 (2019?海安)海边灯塔上的一盏照明灯以固定的规律发出亮光。下图表示前14秒照明灯明暗变化的情况,第1秒是亮的,第2秒是暗的,第3秒是暗的……根据下图,第36秒照明灯是( )的,第52秒照明灯是( )的。
解析:周期规律的问题中首先要搞清楚周期是什么,然后看要求的个数里面有几个这样的周期,还多几个(多下来的几个肯定是从一个周期的第一个开始的),再进行相关计算。注意有时在计算中,要在开头或结尾处去掉非周期的几个数。不难发现本题灯光变化的周期是6秒。36里面正好有6个6,所以是暗的。52里有8个6还余4,看第一个周期里的第4秒即可。
答案:暗 亮
[小试身手]
(2018?息县)25个小球按如下顺序排成一排: 第18个小球是( )球,黑球一共有( )个。
(2019?南充)有249朵花,按照5朵红花、9朵黄花、13朵绿花的顺序循环排列,最后一朵花是( )花。这249朵花中,绿花有( )朵。
黑
16
黄
117
一、填空题。
(2019?岳阳)按规律填空。
(1) (48,8)、(42,7)、(36,6)、( ,5)……
(2) 、、( )、4、( )……
(3) 100%、0.9、 、( )(百分数)、( )(分数)、( )(小数)、( )成……
(4) 0.01a、0.04a、0.09a、( )、0.25a……
(5) 2345、3452、4523、( )……
30
1
0.5
70%
16
四
0.16a
5234
找出规律,填一填。
(1) △□○☆△□○☆△□○☆△□○☆……第33个图形是( )。
(2) △□☆★△△□☆★△△□☆★……当△最多是( )个时,其他三种图形一共是24个。
(2018?三门峡)书架上有3本不同的画报和5本不同的故事书,从书架上取出1本画报和1本故事书,共有( )种不同的取法。
体育课上,六年级(3)班23名男生排成一行,从最左边一人开始,依次按“一、二、三、四”报数(如下图)。
小明排在左起第18个,应该报( );这些男生中,报“一”的有( )名。
△
17
15
二
6
小明按照一定的规律写数:+1、+3、-5、+7、+9、-11、+13、+15、-17……写完第90个数时,他不写了。他写的数中共有( )个正数,( )个负数。
(2019?莆田)如下图,观察下面正三角形的三个顶点所标的数字规律,那么2019这个数在第( )个三角形的( )顶点处(填“上”“左下”“右下”)。
(2018?太仓)元旦时,校园内挂起一串彩灯,每两盏白灯之间依次有红、黄、绿灯各一盏,也就是说从第一盏白灯起,每盏白灯后都紧跟三盏彩灯,第23盏灯是( )灯。
(2019?山东)有一列数:2、5、8、11、14、…,则104在这列数中是第( )个数。
60
30
673
右下
黄
35
下面的四个图形中,数的排列有规律也有联系,则A=( )。
(2019?石家庄)下图中,第四个正方形有( )个点,第五个正方形有( )个点。如果某个正方形每边上的点的个数用a表示,则这个正方形的点的总的个数可表示为( )。
54
16
25
a2
二、 选择题。
(2018?如皋)如图,用小正方体搭图形,从上往下数,第1层需要1块,第2层需要5块,第3层需要9块,像这样,第6层需要( )块小正方体。
A. 25 B. 21
C. 17 D. 14
加法算式1+2、2+5、3+8、1+11、2+14、3+17……是按一定规律排列的,第40个加法算式是( )
A. 1+120 B. 2+119 C. 1+119
(2019?东台)填在下面各正方形中的四个数遵循相同的规律,根据此规律,m的值是( )。
A. 86 B. 52
C. 38 D. 74
B
C
A
填在下面图形中的三个数之间都有相同的规律,根据此规律,a的值是( )。
A. 216 B. 432
C. 900 D. 1080
一个正方形池塘的边长是12米,要在池塘的四周每隔2米栽1棵树,四个顶点各栽1棵,一共要栽( )棵树。
A. 30 B. 28
C. 26 D. 24
C
D
如图,用棱长为1厘米的小正方体可以拼成长方体,10个小正方体拼成的长方体的表面积比原先小正方体的表面积之和减少了( )平方厘米。
A. 10 B. 20
C. 9 D. 18
四个小朋友玩换位置的游戏(他们分别为A、B、C、D),开始时按A、B、C、D分别坐在第1、2、3、4号位置上(如图)。第一次他们前后两排换,第二次左右两排换,第三次又前后两排换,第四次又左右两排换。这样交换下去,第十次换位置后,C在( )号位置上。
A. 1 B. 2
C. 3 D. 4
用1、3、4、5四张数字卡片能摆出( )个不同的两位数。
A. 3 B. 6 C. 9 D. 12
D
D
A
正方形的个数 1 2 3 4 …
拼成图形的周长 ? ? ? ? …
三、解答下面各题。
(2019?盐城)把边长为1的正方形纸片按下面的规律拼成长方形。
填表:
(2) 用6个正方形拼成的长方形的周长是( )。
(3) 用m个正方形拼成的长方形的周长是( )。
2.如图,最大正方形的边长为10厘米,依次连接各正方形四条边的中点,第三次围成的小正方形的面积是多少?
4
14
2m+2
10×10÷2÷2÷2=12.5(平方厘米)
6
8
10
? 第①号
长方形 第②号
长方形 第③号
长方形 第④号
长方形 …
长(cm) 2 3 5 8 …
宽(cm) 1 2 3 ? …
周长(cm) 6 10 16 ? …
3. (2019?如皋)探索规律。
[阅读] 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1、1、2、3、5、8、13、21、34、…,其中从第三个数起,每一个数都等于它前面两个数的和,如3=1+2,5=2+3……
[探究] 现在以这组数中的各个数作为正方形的边长画出正方形,再如下图依次拼成长方形(单位:cm)。
第④号长方形的宽、周长分别是多少?请在表格中填一填。
如果按照这个规律继续画下去,那么第⑧号长方形的周长是( )cm。
5
178
26
专题十 数学思考
第21课时 找规律
考点一 数列的规律
例1 (2019?抚顺)找规律填空:0、1、1、2、3、5、8、13、( )、( )……
解析:这类题目一般先要找出排列的规律,并按规律继续写出几个数,或将中间缺少的数填起来。解答时,需要较强的数感,一般情况下有相邻两个数的和(或差、商)相等或呈现一定的规律,不同数位上的数字按一定的规律排列等。而本题中的数在逐渐变大,但又不是简单地做加上一个固定数的加法,或是所加数在递增的加法。从最前面开始,0+1=1,1+1=2,再接着有1+2=3,2+3=5,3+5=8,5+8=13,8+13=21,13+21=34……
答案:21 34
[小试身手]
(2019?兴化)按规律填数:
(1) 8、11、14、17、( )、23……
(2) 一列数1、2、2、3、3、3、4、4、4、4……中的第35个数是( )。
(2019?泰兴)有一列数:、、、……则第6个数是( ),第n个数是( )。
(2018?四川)先找规律,再填数。
+ -1= , + - , + - = , + - = …则
+ - ( )=
20
8
考点二 图形变化的规律
例2 如图,用“十字形”分割正方形,分割1次,分成了4个正方形;分割2次,分成了7个正方形……如果连续用“十字形”分割20次,那么分成了( )个正方形。如果分成了361个正方形,那么需用“十字形”分割( )次。
解析:可以先从最简单的开始列表格,再去发现其中的规律:
通过分析数据可以发现,如果用“十字形”分割n次,那么正方形的个数为3n+1。分割20次,正方形有 3×20+1=61(个)。分成了361个正方形,需用“十字形”分割(361-1)÷3=120(次)。
答案:61 120
分割次数 0 1 2 3 4 …
正方形的个数 1 4 7 10 13 …
[小试身手]
(2019?杭州)用小棒摆正六边形(如图),摆10个正六边形需要小棒( )根;摆n个正六边形需要小棒( )根。
(2019?淮安)如图都是用同样大小的正三角形按一定规律拼成的一组图形。
(1) 第5个图形中,有( )个白正三角形。
(2) 第( )个图形中,白正三角形比黑正三角形多2019个。
51
5n+1
21
2018
解析:(1) 第1个图形中白正三角形的个数是3,从第2个图形开始,白正三角形的个数依次增加3、4、5、6…… (2) 第n个图形中白正三角形比黑正三角形多(n+1)个。
6. 在下面的方格图中画一条直线,最多能穿过几个方格?
穿过1×1的方格图,最多可穿过( )个方格。
穿过2×2的方格图,最多可穿过( )个方格。
穿过10×10的方格图,最多可穿过( )个方格。
1
3
19
考点三 间隔现象的规律
例3 (2019?武汉)300米长的道路两旁,均每隔30米种1棵树(端点处都种),一共种了多少棵树?每两棵树之间放3张躺椅,一共有多少张躺椅?
解析:根据题意,端点处都种也就是两端都种树,所以树的棵数=间隔数+1。300÷30=10(个)间隔,就有10+1=11(棵)树。然后还有一个关键条件需要注意,路的两旁都种树,所以共有11×2=22(棵)树。每两棵树之间有3张躺椅,即有10×2×3=60(张)躺椅。
答案:300÷30=10(个)
10+1=11(棵)
11×2=22(棵)
10×3×2=60(张)
答:一共种了22棵树,一共有60张躺椅。
运用分类讨论法解题
间隔现象的规律在实际生活中很常见,本题需注意分类讨论,在不封闭图形中,有三种情况:(1) 两端都栽,植树的棵数=间隔数+1;(2) 两端都不栽,植树的棵数=间隔数-1;(3) 一端栽,一端不栽,植树的棵数=间隔数。
[小试身手]
(1) 一条从南往北的河的一边栽了75棵柳树(两端都栽),每两棵柳树之间栽了1棵杨树,杨树栽了( )棵。
(2) 沿圆形池塘的一周栽了75棵柳树,每两棵柳树之间栽了1棵杨树,杨树栽了( )棵。
学校的圆形花坛的周长为32米,每隔 4米放一盆花,共放( )盆花。
A. 7 B. 8 C. 9
(2018?大理)20面小旗插在迎宾道的两旁(两端都插),每相邻两面小旗的距离是10米,这条迎宾道长多少米?
74
75
20÷2=10(面) 10-1=9(个) 10×9=90(米)
B
考点四 搭配的规律
例4 (2019?商丘)从6名候选人中选出2人参加演讲比赛,共有( )种选法。
A. 10 B. 12 C. 15 D. 18
解析:本题要有序思考,不妨将6人依次编号为1、2、3、4、5、6,然后从1开始去选人搭配,1与2、1与3、1与4、1与5、1与6,共5种选法,接着从2去选人搭配,2与3、2与4、2与5、2与6,共4种选法,依此类推,共有3种、2种和1种选法,这样一共有5+4+3+2+1=15(种)。这道题还可以这样想,1人出来选人搭配,共有5种选法,这样6人就有6个5种选法,然后因为重复,再除以2即可。
答案:C
[小试身手]
(2019?广元)学校为艺术节选送节目,要从2个合唱节目中选1个,3个舞蹈节目中选1个,一共有( )种不同的选送方案。
(2019?太仓)有4支足球队进行踢足球比赛,每两支队都要赛一场,一共要赛( )场。有4个小朋友每两人互寄一张贺卡,一共要准备( )张贺卡。
甲、乙、丙、丁四位同学进行乒乓球比赛,每两位同学之间都要比一场,一共要比( )场。如果甲的成绩是两胜一负,乙的成绩是三战全胜,丙的成绩是三战皆负,那么丁的成绩是( )。
6
6
一胜两负
12
6
考点五 周期的规律
例5 (2019?海安)海边灯塔上的一盏照明灯以固定的规律发出亮光。下图表示前14秒照明灯明暗变化的情况,第1秒是亮的,第2秒是暗的,第3秒是暗的……根据下图,第36秒照明灯是( )的,第52秒照明灯是( )的。
解析:周期规律的问题中首先要搞清楚周期是什么,然后看要求的个数里面有几个这样的周期,还多几个(多下来的几个肯定是从一个周期的第一个开始的),再进行相关计算。注意有时在计算中,要在开头或结尾处去掉非周期的几个数。不难发现本题灯光变化的周期是6秒。36里面正好有6个6,所以是暗的。52里有8个6还余4,看第一个周期里的第4秒即可。
答案:暗 亮
[小试身手]
(2018?息县)25个小球按如下顺序排成一排: 第18个小球是( )球,黑球一共有( )个。
(2019?南充)有249朵花,按照5朵红花、9朵黄花、13朵绿花的顺序循环排列,最后一朵花是( )花。这249朵花中,绿花有( )朵。
黑
16
黄
117
一、填空题。
(2019?岳阳)按规律填空。
(1) (48,8)、(42,7)、(36,6)、( ,5)……
(2) 、、( )、4、( )……
(3) 100%、0.9、 、( )(百分数)、( )(分数)、( )(小数)、( )成……
(4) 0.01a、0.04a、0.09a、( )、0.25a……
(5) 2345、3452、4523、( )……
30
1
0.5
70%
16
四
0.16a
5234
找出规律,填一填。
(1) △□○☆△□○☆△□○☆△□○☆……第33个图形是( )。
(2) △□☆★△△□☆★△△□☆★……当△最多是( )个时,其他三种图形一共是24个。
(2018?三门峡)书架上有3本不同的画报和5本不同的故事书,从书架上取出1本画报和1本故事书,共有( )种不同的取法。
体育课上,六年级(3)班23名男生排成一行,从最左边一人开始,依次按“一、二、三、四”报数(如下图)。
小明排在左起第18个,应该报( );这些男生中,报“一”的有( )名。
△
17
15
二
6
小明按照一定的规律写数:+1、+3、-5、+7、+9、-11、+13、+15、-17……写完第90个数时,他不写了。他写的数中共有( )个正数,( )个负数。
(2019?莆田)如下图,观察下面正三角形的三个顶点所标的数字规律,那么2019这个数在第( )个三角形的( )顶点处(填“上”“左下”“右下”)。
(2018?太仓)元旦时,校园内挂起一串彩灯,每两盏白灯之间依次有红、黄、绿灯各一盏,也就是说从第一盏白灯起,每盏白灯后都紧跟三盏彩灯,第23盏灯是( )灯。
(2019?山东)有一列数:2、5、8、11、14、…,则104在这列数中是第( )个数。
60
30
673
右下
黄
35
下面的四个图形中,数的排列有规律也有联系,则A=( )。
(2019?石家庄)下图中,第四个正方形有( )个点,第五个正方形有( )个点。如果某个正方形每边上的点的个数用a表示,则这个正方形的点的总的个数可表示为( )。
54
16
25
a2
二、 选择题。
(2018?如皋)如图,用小正方体搭图形,从上往下数,第1层需要1块,第2层需要5块,第3层需要9块,像这样,第6层需要( )块小正方体。
A. 25 B. 21
C. 17 D. 14
加法算式1+2、2+5、3+8、1+11、2+14、3+17……是按一定规律排列的,第40个加法算式是( )
A. 1+120 B. 2+119 C. 1+119
(2019?东台)填在下面各正方形中的四个数遵循相同的规律,根据此规律,m的值是( )。
A. 86 B. 52
C. 38 D. 74
B
C
A
填在下面图形中的三个数之间都有相同的规律,根据此规律,a的值是( )。
A. 216 B. 432
C. 900 D. 1080
一个正方形池塘的边长是12米,要在池塘的四周每隔2米栽1棵树,四个顶点各栽1棵,一共要栽( )棵树。
A. 30 B. 28
C. 26 D. 24
C
D
如图,用棱长为1厘米的小正方体可以拼成长方体,10个小正方体拼成的长方体的表面积比原先小正方体的表面积之和减少了( )平方厘米。
A. 10 B. 20
C. 9 D. 18
四个小朋友玩换位置的游戏(他们分别为A、B、C、D),开始时按A、B、C、D分别坐在第1、2、3、4号位置上(如图)。第一次他们前后两排换,第二次左右两排换,第三次又前后两排换,第四次又左右两排换。这样交换下去,第十次换位置后,C在( )号位置上。
A. 1 B. 2
C. 3 D. 4
用1、3、4、5四张数字卡片能摆出( )个不同的两位数。
A. 3 B. 6 C. 9 D. 12
D
D
A
正方形的个数 1 2 3 4 …
拼成图形的周长 ? ? ? ? …
三、解答下面各题。
(2019?盐城)把边长为1的正方形纸片按下面的规律拼成长方形。
填表:
(2) 用6个正方形拼成的长方形的周长是( )。
(3) 用m个正方形拼成的长方形的周长是( )。
2.如图,最大正方形的边长为10厘米,依次连接各正方形四条边的中点,第三次围成的小正方形的面积是多少?
4
14
2m+2
10×10÷2÷2÷2=12.5(平方厘米)
6
8
10
? 第①号
长方形 第②号
长方形 第③号
长方形 第④号
长方形 …
长(cm) 2 3 5 8 …
宽(cm) 1 2 3 ? …
周长(cm) 6 10 16 ? …
3. (2019?如皋)探索规律。
[阅读] 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1、1、2、3、5、8、13、21、34、…,其中从第三个数起,每一个数都等于它前面两个数的和,如3=1+2,5=2+3……
[探究] 现在以这组数中的各个数作为正方形的边长画出正方形,再如下图依次拼成长方形(单位:cm)。
第④号长方形的宽、周长分别是多少?请在表格中填一填。
如果按照这个规律继续画下去,那么第⑧号长方形的周长是( )cm。
5
178
26
