2020春人教版八下数学第18.1.1平行四边形的性质教学课件(2课时 21张)
文档属性
| 名称 | 2020春人教版八下数学第18.1.1平行四边形的性质教学课件(2课时 21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 303.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 00:00:00 | ||
图片预览


文档简介
课件21张PPT。第1课时 平行四边形的边、角特征第十八章 平行四边形
18.1 平行四边形
18.1.1 平行四边形的性质目习标1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
3.培养学生发现问题、解决问题的能力及逻辑推理能力.反习馈阅读教材P41~43,完成下列问题.
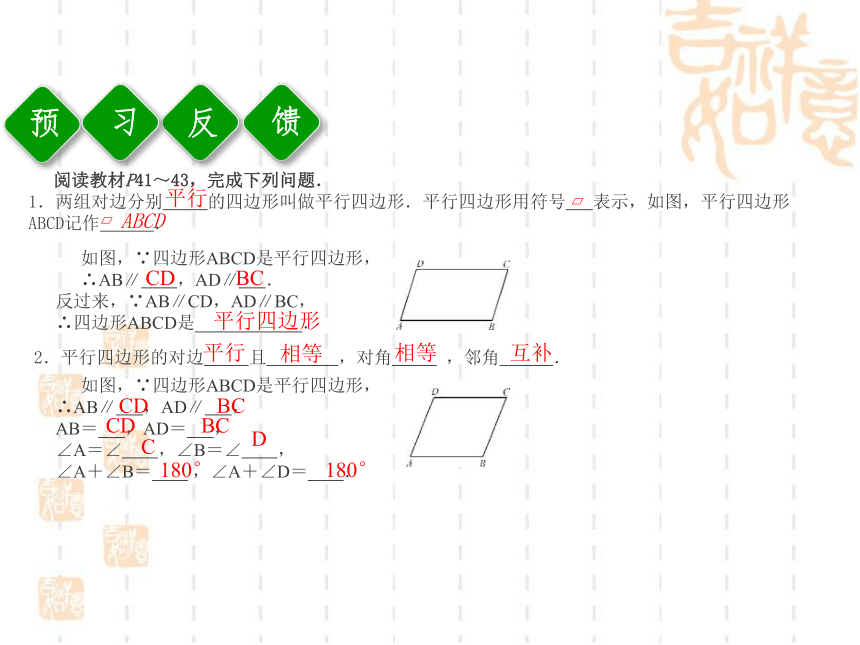
1.两组对边分别 的四边形叫做平行四边形.平行四边形用符号 表示,如图,平行四边形ABCD记作 .如图,∵四边形ABCD是平行四边形,
∴AB∥ ,AD∥ .
反过来,∵AB∥CD,AD∥BC,
∴四边形ABCD是 .平行??ABCDCDBC平行四边形如图,∵四边形ABCD是平行四边形,
∴AB∥ ,AD∥ ,
AB= ,AD= ,
∠A=∠ ,∠B=∠ ,
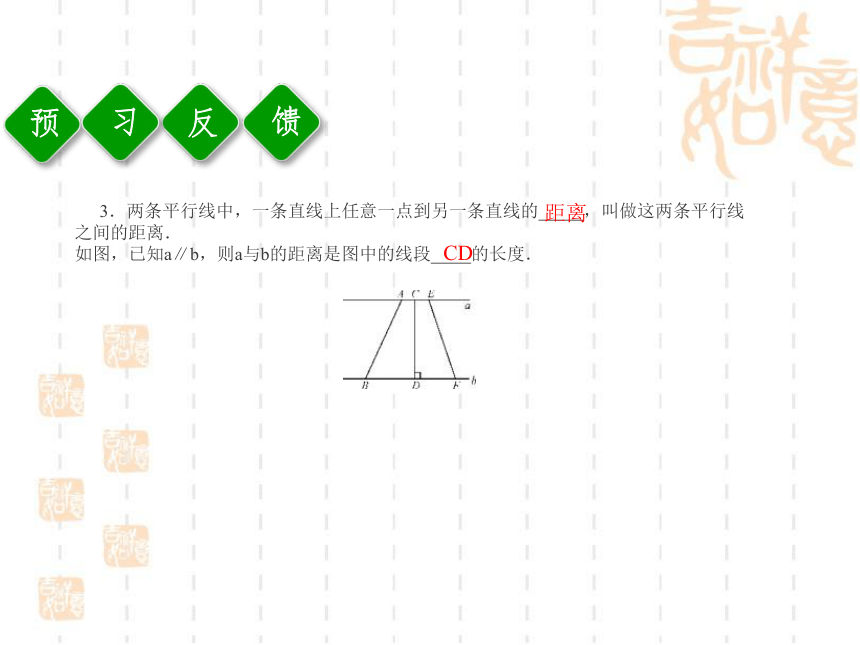
∠A+∠B= ,∠A+∠D= .2.平行四边形的对边 且 ,对角 ,邻角 .平行相等相等互补CDCDBCBCCD180°180°反习馈3.两条平行线中,一条直线上任意一点到另一条直线的 ,叫做这两条平行线之间的距离.
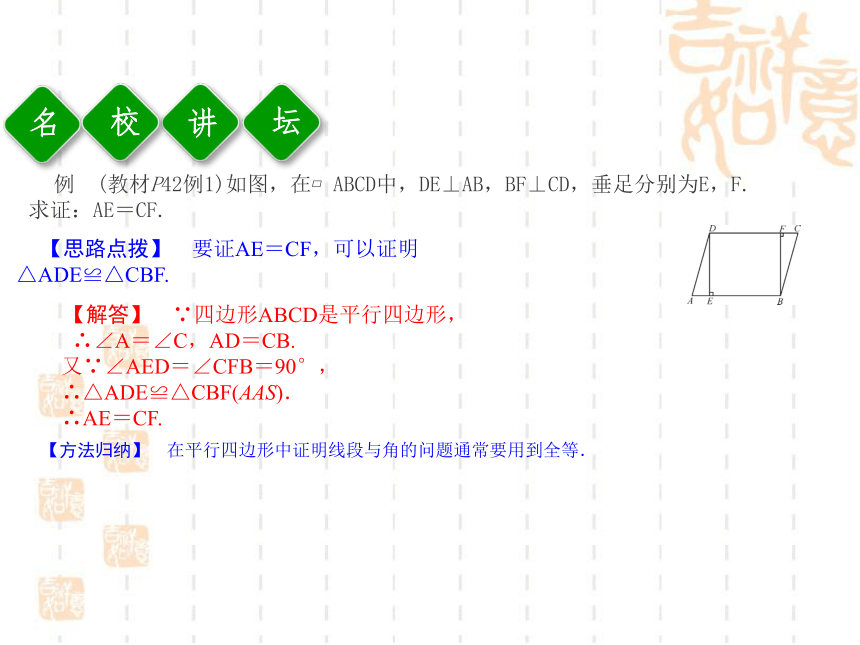
如图,已知a∥b,则a与b的距离是图中的线段 的长度.距离CD讲校坛例 (教材P42例1)如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.【思路点拨】 要证AE=CF,可以证明△ADE≌△CBF.【解答】 ∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS).
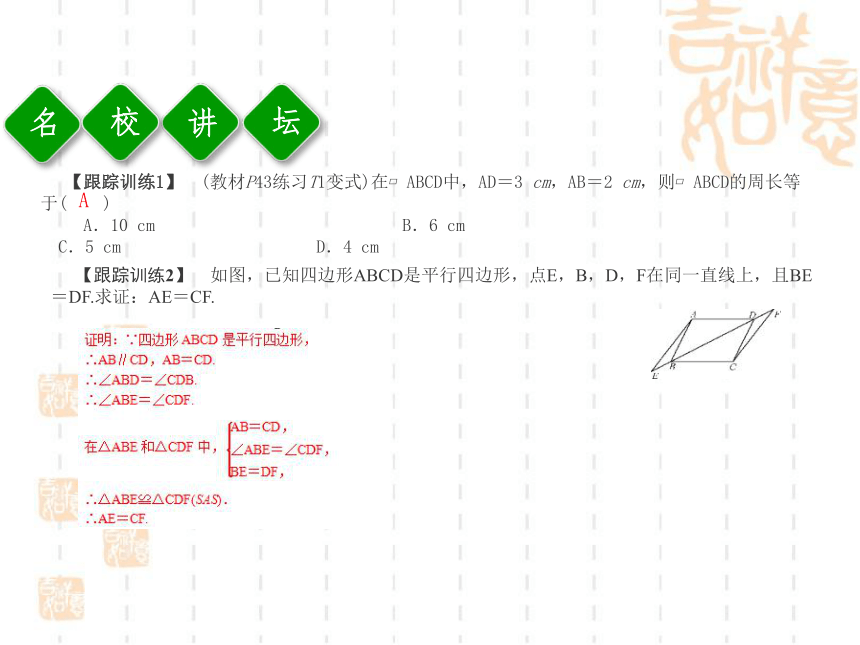
∴AE=CF.【方法归纳】 在平行四边形中证明线段与角的问题通常要用到全等.讲校坛【跟踪训练1】 (教材P43练习T1变式)在?ABCD中,AD=3 cm,AB=2 cm,则?ABCD的周长等于( )
A.10 cm B.6 cm
C.5 cm D.4 cm【跟踪训练2】 如图,已知四边形ABCD是平行四边形,点E,B,D,F在同一直线上,且BE=DF.求证:AE=CF.
A训固练1.已知在?ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
2.如图,在?ABCD中,AB=3,BC=5,∠ABC的平分线交AD于点E,则DE的长为( )
3.若平行四边形中两个内角的度数比为1∶2,则其中较大的内角是( )
A.45° B.60° C.90° D.120°
4.在?ABCD中,若AB=3 cm,AD=4 cm,则?ABCD的周长为 .
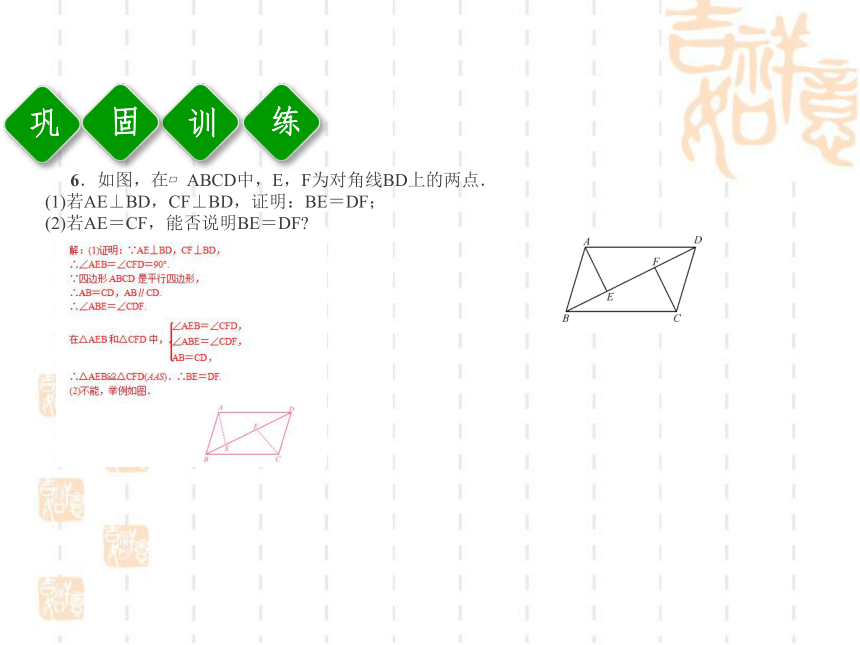
5.在平面直角坐标系中,若?ABCD的三个顶点坐标为A(1,0),B(0,2),C(-4,2),则另外一个顶点D的坐标为 . A.5 B.4 C.3 D.2BDD14 cm(-3,0)训固练6.如图,在?ABCD中,E,F为对角线BD上的两点.
(1)若AE⊥BD,CF⊥BD,证明:BE=DF;
(2)若AE=CF,能否说明BE=DF?小堂结第2课时 平行四边形的对角线性质目习标1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2.能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.
3.培养学生的推理论证能力和逻辑思维能力.反习馈阅读教材P43~44,完成下列问题.
1.平行四边形的对角线 .
如图,∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,
∴AO= = ,BO= = .互相平分OCACDOBD2.(1)平行四边形的面积=底× .
如图1,在?ABCD中,AE⊥BC于E,AF⊥CD于F,则S?ABCD=BC·
=CD· .AEAF(2)如图2,?ABCD的对角线AC,BD相交于点O,则S△AOB S△BOC S△COD S△DOA
S?ABCD.====高 讲校坛例 (教材P44例2)如图,在?ABCD中,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长,以及?ABCD的面积.【思路点拨】 根据平行四边形的性质即可得到BC和CD的长,根据AC⊥BC,在Rt△ABC中运用勾股定理即可得出AC的长,又OA等于AC的一半即可求出OA,?ABCD的面积=BC·AC.讲校坛【跟踪训练1】 (教材P44练习T1)如图,在?ABCD中,BC=10,AC=8,BD=14.△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?讲校坛【跟踪训练2】 (《名校课堂》18.1.1第2课时习题)如图所示,在?ABCD中,对角线AC与BD相交于点O,点M,N在对角线AC上,且AM=CN,求证:BM∥DN.训固练1.如图,?ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB2.如图,?ABCD的对角线AC和BD相交于点O,与△OBC面积相等的三角形(不包括自身)的个数是( )
A.4 B.3 C.2 D.1CB训固练3.如图,在?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD=( )
A.61° B.63° C.65° D.67°
4.如图,在?ABCD中,∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( )
A.4 cm B.5 cm C.6 cm D.8 cmCA5.已知在?ABCD中,AC,BD交于点O,△AOB的面积为2,那么?ABCD的面积为 .8训固练6.如图,已知?ABCD的对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,求证:△ADE≌△CBF.
训固练7.如图,在?ABCD中,对角线AC,BD交于点O,过点O作直线EF,交AD,BC于点E,F.
(1)求证:OE=OF;
(2)四边形ABFE的面积与四边形FCDE的面积间有何关系?小堂结THANK YOU!
18.1 平行四边形
18.1.1 平行四边形的性质目习标1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
3.培养学生发现问题、解决问题的能力及逻辑推理能力.反习馈阅读教材P41~43,完成下列问题.
1.两组对边分别 的四边形叫做平行四边形.平行四边形用符号 表示,如图,平行四边形ABCD记作 .如图,∵四边形ABCD是平行四边形,
∴AB∥ ,AD∥ .
反过来,∵AB∥CD,AD∥BC,
∴四边形ABCD是 .平行??ABCDCDBC平行四边形如图,∵四边形ABCD是平行四边形,
∴AB∥ ,AD∥ ,
AB= ,AD= ,
∠A=∠ ,∠B=∠ ,
∠A+∠B= ,∠A+∠D= .2.平行四边形的对边 且 ,对角 ,邻角 .平行相等相等互补CDCDBCBCCD180°180°反习馈3.两条平行线中,一条直线上任意一点到另一条直线的 ,叫做这两条平行线之间的距离.
如图,已知a∥b,则a与b的距离是图中的线段 的长度.距离CD讲校坛例 (教材P42例1)如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.【思路点拨】 要证AE=CF,可以证明△ADE≌△CBF.【解答】 ∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
又∵∠AED=∠CFB=90°,
∴△ADE≌△CBF(AAS).
∴AE=CF.【方法归纳】 在平行四边形中证明线段与角的问题通常要用到全等.讲校坛【跟踪训练1】 (教材P43练习T1变式)在?ABCD中,AD=3 cm,AB=2 cm,则?ABCD的周长等于( )
A.10 cm B.6 cm
C.5 cm D.4 cm【跟踪训练2】 如图,已知四边形ABCD是平行四边形,点E,B,D,F在同一直线上,且BE=DF.求证:AE=CF.
A训固练1.已知在?ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
2.如图,在?ABCD中,AB=3,BC=5,∠ABC的平分线交AD于点E,则DE的长为( )
3.若平行四边形中两个内角的度数比为1∶2,则其中较大的内角是( )
A.45° B.60° C.90° D.120°
4.在?ABCD中,若AB=3 cm,AD=4 cm,则?ABCD的周长为 .
5.在平面直角坐标系中,若?ABCD的三个顶点坐标为A(1,0),B(0,2),C(-4,2),则另外一个顶点D的坐标为 . A.5 B.4 C.3 D.2BDD14 cm(-3,0)训固练6.如图,在?ABCD中,E,F为对角线BD上的两点.
(1)若AE⊥BD,CF⊥BD,证明:BE=DF;
(2)若AE=CF,能否说明BE=DF?小堂结第2课时 平行四边形的对角线性质目习标1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2.能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.
3.培养学生的推理论证能力和逻辑思维能力.反习馈阅读教材P43~44,完成下列问题.
1.平行四边形的对角线 .
如图,∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,
∴AO= = ,BO= = .互相平分OCACDOBD2.(1)平行四边形的面积=底× .
如图1,在?ABCD中,AE⊥BC于E,AF⊥CD于F,则S?ABCD=BC·
=CD· .AEAF(2)如图2,?ABCD的对角线AC,BD相交于点O,则S△AOB S△BOC S△COD S△DOA
S?ABCD.====高 讲校坛例 (教材P44例2)如图,在?ABCD中,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长,以及?ABCD的面积.【思路点拨】 根据平行四边形的性质即可得到BC和CD的长,根据AC⊥BC,在Rt△ABC中运用勾股定理即可得出AC的长,又OA等于AC的一半即可求出OA,?ABCD的面积=BC·AC.讲校坛【跟踪训练1】 (教材P44练习T1)如图,在?ABCD中,BC=10,AC=8,BD=14.△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?讲校坛【跟踪训练2】 (《名校课堂》18.1.1第2课时习题)如图所示,在?ABCD中,对角线AC与BD相交于点O,点M,N在对角线AC上,且AM=CN,求证:BM∥DN.训固练1.如图,?ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB2.如图,?ABCD的对角线AC和BD相交于点O,与△OBC面积相等的三角形(不包括自身)的个数是( )
A.4 B.3 C.2 D.1CB训固练3.如图,在?ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD=( )
A.61° B.63° C.65° D.67°
4.如图,在?ABCD中,∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( )
A.4 cm B.5 cm C.6 cm D.8 cmCA5.已知在?ABCD中,AC,BD交于点O,△AOB的面积为2,那么?ABCD的面积为 .8训固练6.如图,已知?ABCD的对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,求证:△ADE≌△CBF.
训固练7.如图,在?ABCD中,对角线AC,BD交于点O,过点O作直线EF,交AD,BC于点E,F.
(1)求证:OE=OF;
(2)四边形ABFE的面积与四边形FCDE的面积间有何关系?小堂结THANK YOU!
