高中数学人教新课标A选修4-2第三讲逆变换与逆矩阵二 二阶行列式与逆矩阵(共27张PPT)
文档属性
| 名称 | 高中数学人教新课标A选修4-2第三讲逆变换与逆矩阵二 二阶行列式与逆矩阵(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 881.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 14:48:53 | ||
图片预览







文档简介
(共27张PPT)
我们已经知道二阶矩阵不一定可逆,但如何判断它是否可逆?如何求它的逆呢?
掌握判断矩阵是否可逆的方法
会求逆矩阵
搞清二阶行列式与二阶矩阵的区别
通过从特殊到一般的过程,体会逆矩阵的存在性及求法
培养学生的从一般到特殊的归纳,总结和类比的能力,获得新知
用行列式是求逆矩阵
用变换的观点认识解二元一次方程组的意义,并会用系数矩阵的逆矩阵解系数矩阵可逆的二元一次方程组
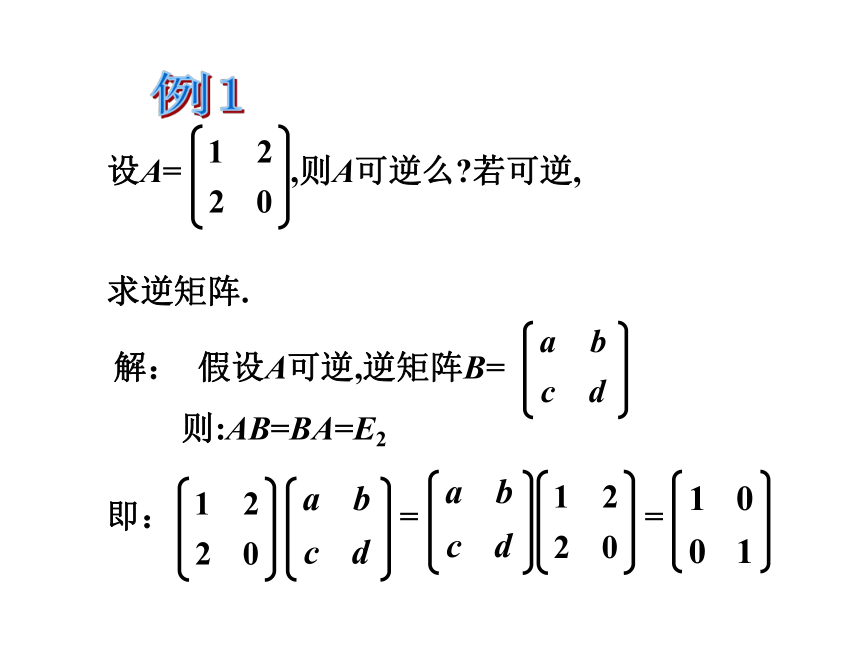
则:AB=BA=E2
则:AB=BA=E2
无解.
∴矩阵A的逆矩阵不存在.
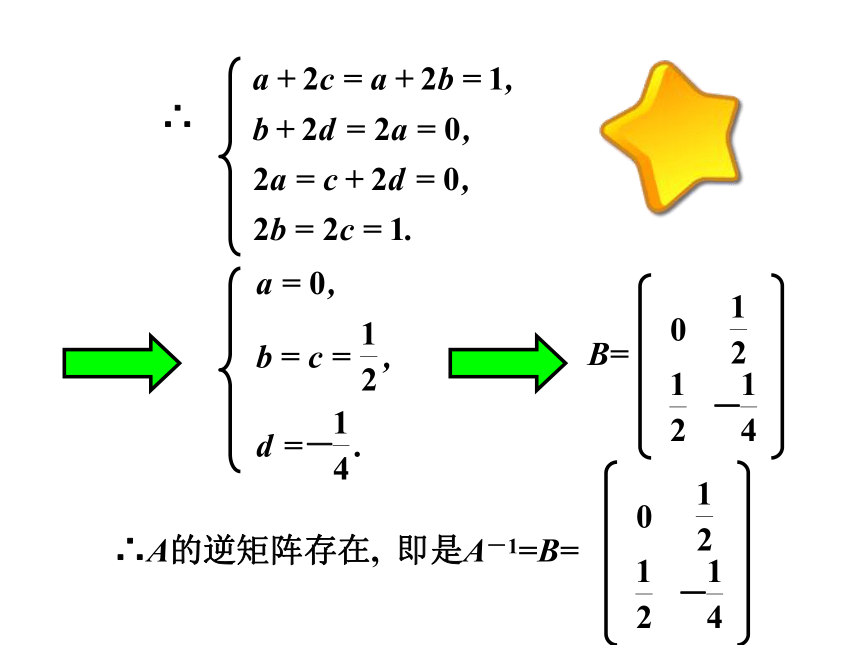
例1中A的对角线上的数相乘再相减不等于0
例2中A的对角线上的数相乘再相减等于0.
解: 设A是可逆的,逆矩阵B=
则有AB=BA=E2.
当det A=ad-bc≠0时,由
-3
18
11
解: (1) 原式=(1-λ)(2-λ)-3×2
=λ2-3λ-4
二阶矩阵仅仅是一个数表,二阶行列式表示一个数或代数式.
∴当k≠1时,矩阵A可逆.
3.矩阵可逆的条件是一个充要条件.
2.二阶矩阵仅仅是一个数表,二阶行列式表示一个数或代数式.
6
☆
■■
汤
我们已经知道二阶矩阵不一定可逆,但如何判断它是否可逆?如何求它的逆呢?
掌握判断矩阵是否可逆的方法
会求逆矩阵
搞清二阶行列式与二阶矩阵的区别
通过从特殊到一般的过程,体会逆矩阵的存在性及求法
培养学生的从一般到特殊的归纳,总结和类比的能力,获得新知
用行列式是求逆矩阵
用变换的观点认识解二元一次方程组的意义,并会用系数矩阵的逆矩阵解系数矩阵可逆的二元一次方程组
则:AB=BA=E2
则:AB=BA=E2
无解.
∴矩阵A的逆矩阵不存在.
例1中A的对角线上的数相乘再相减不等于0
例2中A的对角线上的数相乘再相减等于0.
解: 设A是可逆的,逆矩阵B=
则有AB=BA=E2.
当det A=ad-bc≠0时,由
-3
18
11
解: (1) 原式=(1-λ)(2-λ)-3×2
=λ2-3λ-4
二阶矩阵仅仅是一个数表,二阶行列式表示一个数或代数式.
∴当k≠1时,矩阵A可逆.
3.矩阵可逆的条件是一个充要条件.
2.二阶矩阵仅仅是一个数表,二阶行列式表示一个数或代数式.
6
☆
■■
汤
