高中数学人教新课标A版选修4-2第四讲变换的不变量与矩阵的特征向量二 特征向量的应用(共30张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修4-2第四讲变换的不变量与矩阵的特征向量二 特征向量的应用(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 14:47:52 | ||
图片预览





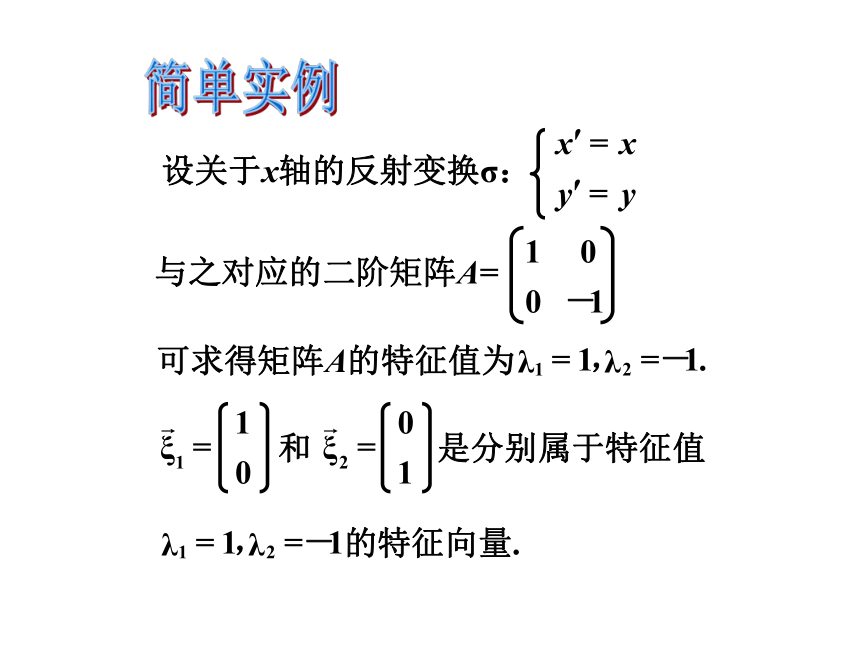






文档简介
(共30张PPT)
特征向量在实际问题的应用.
对于任意的正整数n
……
证明:(1)当n=1时
∴性质1成立;
(2)假设当n = k-1时性质1成立,即:
当n=k时
∴当n=k 时,性质1成立.
在扩散理论中的应用
设某物质能以液态和气态的混合状态存在,又假设在任意一分钟内
(1)液态的5%蒸发成气态;
(2)气态的1%凝结成液态.
现在这些物质中70%是气态的.
求:1分钟以后气态物质占总物质的比例是多少?2分钟?10分钟?最终的情况如何?
记总物质为N.
⑴ 1分钟后
气态物质:
液态物质:
即:
矩阵表示形式:
矩阵P 描述了1分钟以后气态物质和液态物质的转变情况
类似上述推导过程得:
……
③
④
∴1分钟以后,气态物质占总物质的70.8%,
液态物质占总物质的29.2%.
由②式得:
(2) 2分钟后
∴2分钟以后,气态物质占总物质的71.6%,
液态物质占总物质的28.4%.
(3) 10分钟后
利用性质1
即:
由性质1得
∴10分钟以后,气态物质占总物质的76.2%,
液态物质占总物质的23.8%.
∴对任意的自然数n ,由性质1得
解: 矩阵A的特征多项式:
同理:
由性质1得
2.证明:(1)矩阵P的特征多项式为
3.略.
特征向量在实际问题的应用.
对于任意的正整数n
……
证明:(1)当n=1时
∴性质1成立;
(2)假设当n = k-1时性质1成立,即:
当n=k时
∴当n=k 时,性质1成立.
在扩散理论中的应用
设某物质能以液态和气态的混合状态存在,又假设在任意一分钟内
(1)液态的5%蒸发成气态;
(2)气态的1%凝结成液态.
现在这些物质中70%是气态的.
求:1分钟以后气态物质占总物质的比例是多少?2分钟?10分钟?最终的情况如何?
记总物质为N.
⑴ 1分钟后
气态物质:
液态物质:
即:
矩阵表示形式:
矩阵P 描述了1分钟以后气态物质和液态物质的转变情况
类似上述推导过程得:
……
③
④
∴1分钟以后,气态物质占总物质的70.8%,
液态物质占总物质的29.2%.
由②式得:
(2) 2分钟后
∴2分钟以后,气态物质占总物质的71.6%,
液态物质占总物质的28.4%.
(3) 10分钟后
利用性质1
即:
由性质1得
∴10分钟以后,气态物质占总物质的76.2%,
液态物质占总物质的23.8%.
∴对任意的自然数n ,由性质1得
解: 矩阵A的特征多项式:
同理:
由性质1得
2.证明:(1)矩阵P的特征多项式为
3.略.
