冀教版数学八年级下册21.4 一次函数的应用 第1课时 课件(26张ppt)
文档属性
| 名称 | 冀教版数学八年级下册21.4 一次函数的应用 第1课时 课件(26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 00:00:00 | ||
图片预览






文档简介
课件26张PPT。第二十一章
一次函数21.4 一次函数的应用
第1课时冀教版数学八年级下册1.会根据问题情境的数量关系建立相应的一次函数表达式.(重点)
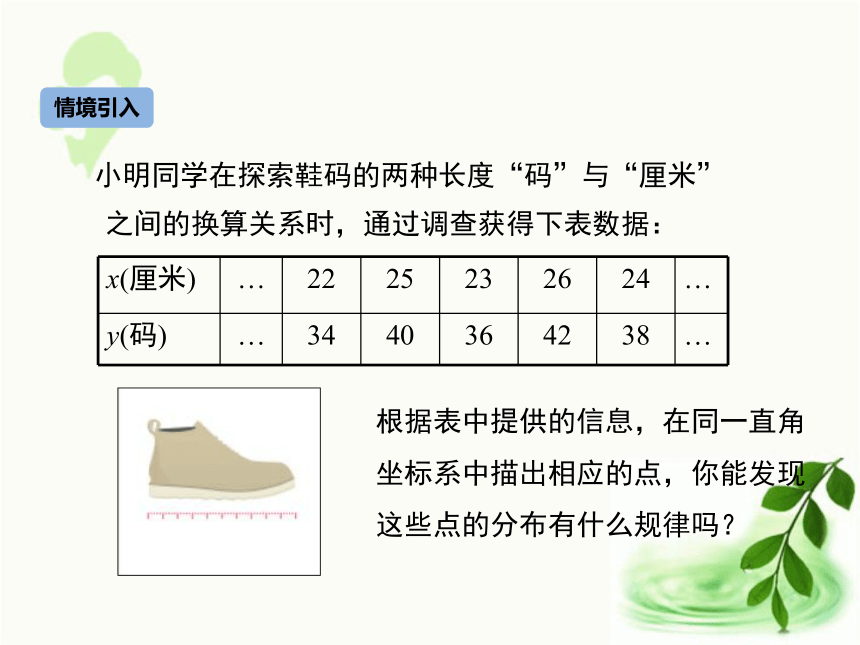
2.能利用一次函数的相关性质解决简单的实际问题.(难点)学习目标情境引入 小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?3032383634424023252421222726y (码)x(厘米)据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?52码,你是怎么判断的呢?O例1.某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.1.设某销售员销售产品x件,他应得的工资记为y元.求y与x之间的函数关系式.y=10x+3000典例精析2.用求出的函数关系式,解决下列问题
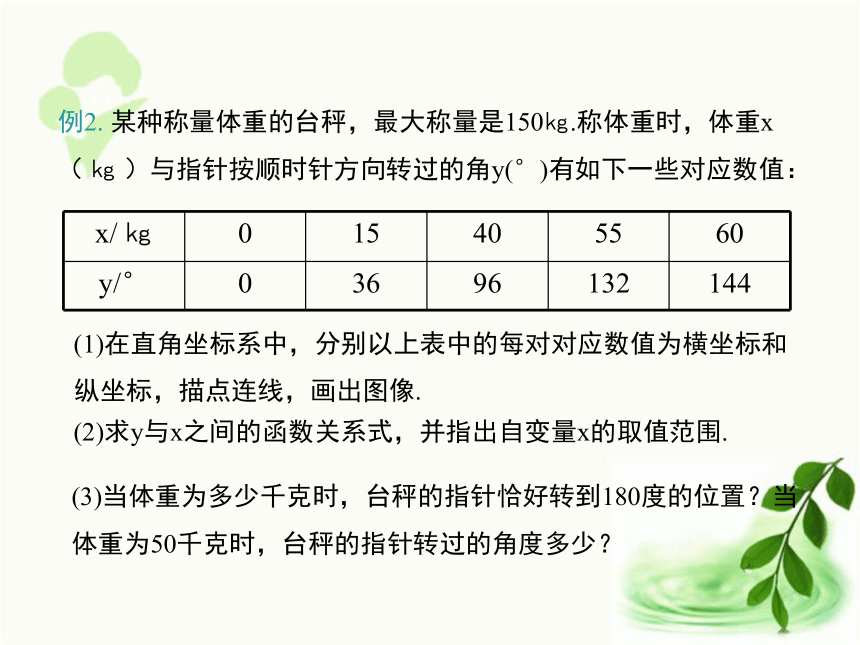
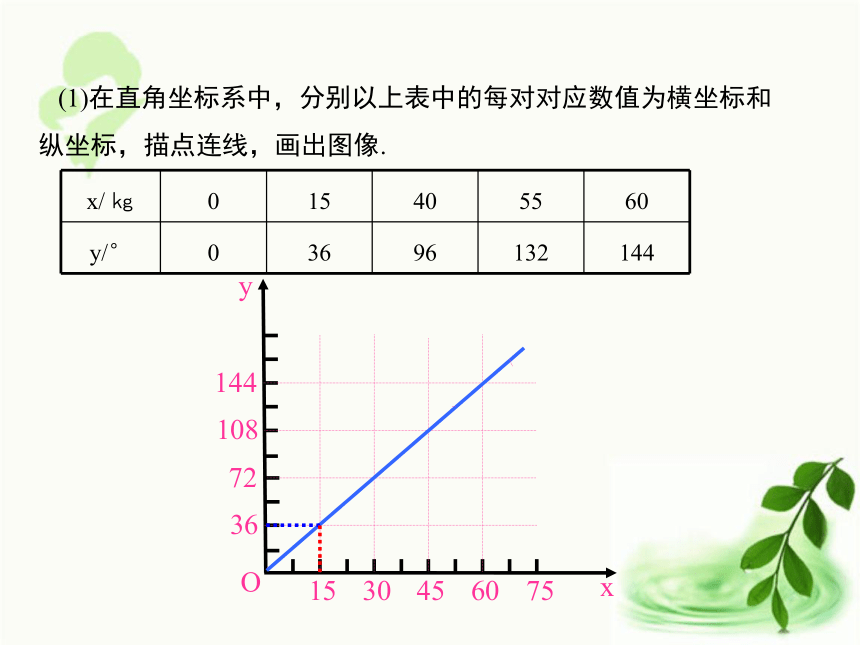
(1)某销售员的工资为4100元,他这个月销售了多少件产品?当y=4100时,4100=10x+3000.解得x=110.(2)要使月工资超过4500元,该月的销售量应当超过多少件?由题意得10x+3000>4500.解得x>150.例2. 某种称量体重的台秤,最大称量是150㎏.称体重时,体重x( ㎏ )与指针按顺时针方向转过的角y(°)有如下一些对应数值: (1)在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像.(2)求y与x之间的函数关系式,并指出自变量x的取值范围.(3)当体重为多少千克时,台秤的指针恰好转到180度的位置?当体重为50千克时,台秤的指针转过的角度多少?xyO15304560753614472108 (1)在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像. (2)求y与x之间的函数关系式,并指出自变量x的取值范围. 分析:由表格给出的数据可以看出,每增加5千克,台秤的指针按顺时针方向旋转12度,所以y是x的正比例函数.根据条件可得y=12/5x(0≤x≤150)(3)当体重为多少千克时,台秤的指针恰好转到180度的位置?当体重为50千克时,台秤的指针转过的角度多少?当y=180时,180=12/5x.解得x=75
当x=50时,y=12/5×50=120.
即当体重为75千克时,台秤的指针恰好转到180度的位置.当体重为50千克时,台秤的指针转过的角度是120度. A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元;从B市调运一台机器到C村和D村的运费分别是300元和500元.
① 设B市运往C市机器x台,求总运费W(元)关于x的函数关系式.② 求总运费最低的调运方案的最低运费是多少.例3.分析① :A 市和 B 市库存机器共:( )台,C 村和D 村共需( )台,B 市运到 C 村 台, B 市剩余 台运到 D 村A 市运到 C 村 台, A 市剩余 台运到 D 村.x(10-x)〔 12-(10-x)〕(6-x)分析② :先求出总运费的关系式,再对照一次函数最值相关问题具体分析.12+610+8解:① B 市运往 C 市机器x台,则有题意可知:
W = 300x + 500 (6-x) + 400(10-x) +800〔12-(10-x)〕
= 200 x + 8600 ( 0 ≤ x ≤ 6 )
∴总运费W(元)关于x的函数关系式为:
W = 200 x + 8600 ( 0 ≤ x ≤ 6 )② ∵ W = 200 x + 8600 ( 0 ≤ x ≤ 6 )是一次函数,且W随x的增大而增大
∴当 x取最小值时,W 有最大值
即当 x = 0 时,W = 8600元
∴ 总运费最低的调运方案的最低运费是8600元 一次函数“最大值”和“最小值”的产生和自变量的取值范围相辅相成:
k > 0 ,a ≤ x ≤ c 时:
x = a 时,y = ka + b 就是最小值,x = c 时,y = kc + b 就是最大值;
k < 0 ,a ≤ x ≤ c 时:
x = a 时, y = ka + b 就是最大值,x = c 时, y = kc+ b 就是最小值.方法归纳例4.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数关系式;
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量. 分析:
(1)x≤8时,每立方米收费(1+0.3)元;
(2)x>8时,超过的部分每立方米收费(1.5+1.2)元. 解:(1)y关于x的函数关系式为:(2)当x=10时,y=2.7×10-11.2=15.8.(3)因为1.3×8=10.4<26.6,所以该用户用水量超过8立方米.所以2.7x-11.2=26.6,解得x=14答:应缴水费为15.8元答:该户这月用水量为14吨总结归纳在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用. 某市出租车的收费标准:不超过3km计费为7元,3km后按2.4元/km计费.(1)写出车费y(元)与路程x(km)之间的函数关系式;(1)当03km时, y=7+2.4(x-3) (2)小亮乘出租车出行,付费12.3元,你能算出小亮乘车的路程吗?(精确到0.1km)∵12.3>7 ∴12.3=7+2.4(x-3) x=5.2(km)做一做1.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:(1) 求身高y与指距x之间的函数关系式;
(2) 当李华的指距为22cm时,你能预测他的身高吗?分析:上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以尝试建立一次函数模型.当堂练习(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解:当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗?2.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数关系式;解:当0≤x≤50 时,由图象可设 y=k1x,∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;
当x>50时,由图象可设 y=k2x+b,∵其经过(50,25)、(100,70),得k2=0.9,b=-20,∴y=0.9x-20.255075100255070100Oy(元)x(度)75⑵根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准是多少?解:不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算.课堂小结简单的一次函数的应用求一次函数的表达式及其应用分段函数的应用谢谢!
一次函数21.4 一次函数的应用
第1课时冀教版数学八年级下册1.会根据问题情境的数量关系建立相应的一次函数表达式.(重点)
2.能利用一次函数的相关性质解决简单的实际问题.(难点)学习目标情境引入 小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?3032383634424023252421222726y (码)x(厘米)据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?52码,你是怎么判断的呢?O例1.某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.1.设某销售员销售产品x件,他应得的工资记为y元.求y与x之间的函数关系式.y=10x+3000典例精析2.用求出的函数关系式,解决下列问题
(1)某销售员的工资为4100元,他这个月销售了多少件产品?当y=4100时,4100=10x+3000.解得x=110.(2)要使月工资超过4500元,该月的销售量应当超过多少件?由题意得10x+3000>4500.解得x>150.例2. 某种称量体重的台秤,最大称量是150㎏.称体重时,体重x( ㎏ )与指针按顺时针方向转过的角y(°)有如下一些对应数值: (1)在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像.(2)求y与x之间的函数关系式,并指出自变量x的取值范围.(3)当体重为多少千克时,台秤的指针恰好转到180度的位置?当体重为50千克时,台秤的指针转过的角度多少?xyO15304560753614472108 (1)在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像. (2)求y与x之间的函数关系式,并指出自变量x的取值范围. 分析:由表格给出的数据可以看出,每增加5千克,台秤的指针按顺时针方向旋转12度,所以y是x的正比例函数.根据条件可得y=12/5x(0≤x≤150)(3)当体重为多少千克时,台秤的指针恰好转到180度的位置?当体重为50千克时,台秤的指针转过的角度多少?当y=180时,180=12/5x.解得x=75
当x=50时,y=12/5×50=120.
即当体重为75千克时,台秤的指针恰好转到180度的位置.当体重为50千克时,台秤的指针转过的角度是120度. A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元;从B市调运一台机器到C村和D村的运费分别是300元和500元.
① 设B市运往C市机器x台,求总运费W(元)关于x的函数关系式.② 求总运费最低的调运方案的最低运费是多少.例3.分析① :A 市和 B 市库存机器共:( )台,C 村和D 村共需( )台,B 市运到 C 村 台, B 市剩余 台运到 D 村A 市运到 C 村 台, A 市剩余 台运到 D 村.x(10-x)〔 12-(10-x)〕(6-x)分析② :先求出总运费的关系式,再对照一次函数最值相关问题具体分析.12+610+8解:① B 市运往 C 市机器x台,则有题意可知:
W = 300x + 500 (6-x) + 400(10-x) +800〔12-(10-x)〕
= 200 x + 8600 ( 0 ≤ x ≤ 6 )
∴总运费W(元)关于x的函数关系式为:
W = 200 x + 8600 ( 0 ≤ x ≤ 6 )② ∵ W = 200 x + 8600 ( 0 ≤ x ≤ 6 )是一次函数,且W随x的增大而增大
∴当 x取最小值时,W 有最大值
即当 x = 0 时,W = 8600元
∴ 总运费最低的调运方案的最低运费是8600元 一次函数“最大值”和“最小值”的产生和自变量的取值范围相辅相成:
k > 0 ,a ≤ x ≤ c 时:
x = a 时,y = ka + b 就是最小值,x = c 时,y = kc + b 就是最大值;
k < 0 ,a ≤ x ≤ c 时:
x = a 时, y = ka + b 就是最大值,x = c 时, y = kc+ b 就是最小值.方法归纳例4.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数关系式;
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量. 分析:
(1)x≤8时,每立方米收费(1+0.3)元;
(2)x>8时,超过的部分每立方米收费(1.5+1.2)元. 解:(1)y关于x的函数关系式为:(2)当x=10时,y=2.7×10-11.2=15.8.(3)因为1.3×8=10.4<26.6,所以该用户用水量超过8立方米.所以2.7x-11.2=26.6,解得x=14答:应缴水费为15.8元答:该户这月用水量为14吨总结归纳在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用. 某市出租车的收费标准:不超过3km计费为7元,3km后按2.4元/km计费.(1)写出车费y(元)与路程x(km)之间的函数关系式;(1)当0
(2) 当李华的指距为22cm时,你能预测他的身高吗?分析:上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以尝试建立一次函数模型.当堂练习(1) 求身高y与指距x之间的函数表达式;解得k = 9, b = -20.
于是y = 9x -20. ①将x = 21,y = 169代入①式也符合.
公式①就是身高y与指距x之间的函数表达式.解:当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.(2) 当李华的指距为22cm时,你能预测他的身高吗?2.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数关系式;解:当0≤x≤50 时,由图象可设 y=k1x,∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;
当x>50时,由图象可设 y=k2x+b,∵其经过(50,25)、(100,70),得k2=0.9,b=-20,∴y=0.9x-20.255075100255070100Oy(元)x(度)75⑵根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准是多少?解:不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算.课堂小结简单的一次函数的应用求一次函数的表达式及其应用分段函数的应用谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
