冀教版数学八年级下册21.4 一次函数的应用 第2课时 课件(23张ppt)
文档属性
| 名称 | 冀教版数学八年级下册21.4 一次函数的应用 第2课时 课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 00:00:00 | ||
图片预览







文档简介
课件23张PPT。第二十一章
一次函数21.4 一次函数的应用
第2课时冀教版数学八年级下册1.会根据问题情境的数量关系建立相应的一次函数表达式.
(重点)
2.能利用两个一次函数解决实际问题.(难点)学习目标问题引入老师为了教学,需要在家上网查资料.电信公司提供了两种上网收费方式:
方式 1 :按上网时间以每小时 1 元计费;
方式 2 :月租费 20 元,再按上网时间以每小时 0.6 元计费.
请同学们帮老师选择:
以何种方式上网更合算?典例精析由于小红比小明晚出发2 h,因此小红所用时间为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3. (1)分别写出y1 ,y2与x之间的函数表达式;过点(0,40)作射线l 与x 轴平行,它先与射线
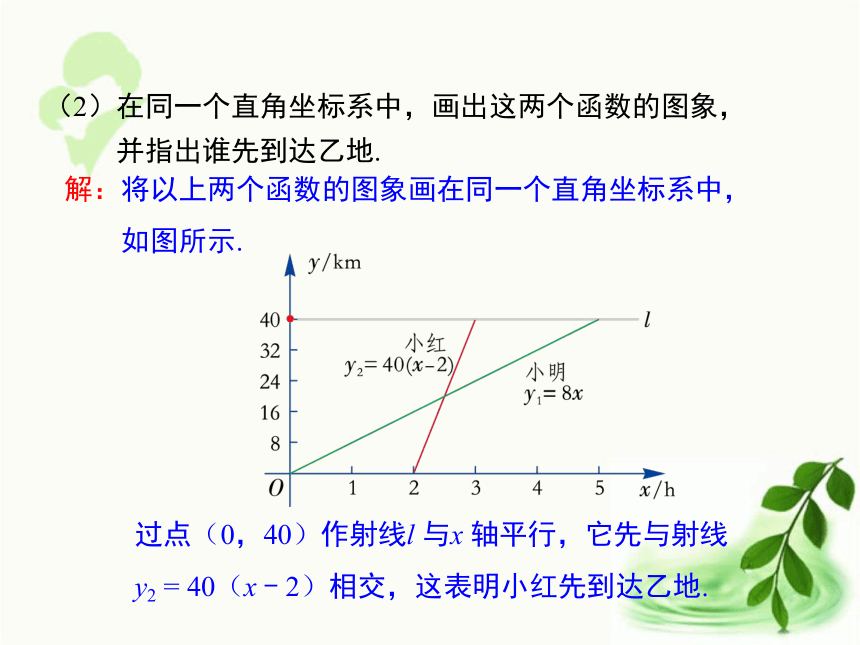
y2 = 40(x - 2)相交,这表明小红先到达乙地. (2)在同一个直角坐标系中,画出这两个函数的图象,
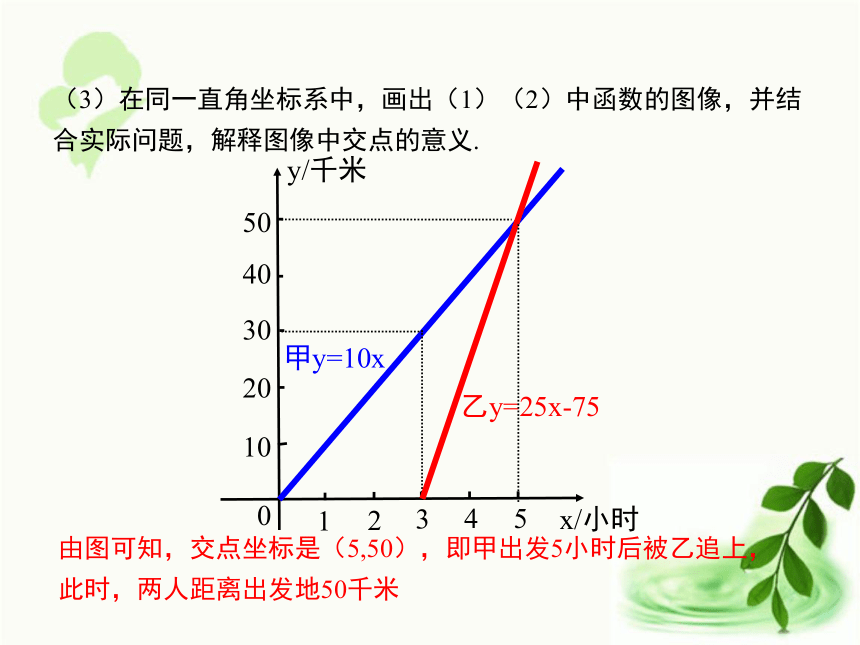
并指出谁先到达乙地.甲骑自行车以10千米每小时的速度沿公路行驶,出发3小时后,乙骑摩托车从同一地点出发沿公路与甲同向行驶,速度为25千米每小时.设甲离开出发地的时间为x小时.(2)写出乙离开出发地的路程y与x之间的函数关系式,并指出自变量x的取值范围;y=10x(x≥0)y=25x-75(x≥3)做一做(1)写出甲离开出发地的路程y与x之间的函数关系式,并指出自变量x的取值范围;y/千米0x/小时532110504030204甲y=10x乙y=25x-75由图可知,交点坐标是(5,50),即甲出发5小时后被乙追上,此时,两人距离出发地50千米(3)在同一直角坐标系中,画出(1)(2)中函数的图像,并结合实际问题,解释图像中交点的意义.例2 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少? 分析:假设该单位参加旅游人数为x,按甲旅行社的优惠条件,应付费用80x 元;按乙旅行社的优惠条件,应付费用(60x+1000)元.问题变为比较80x 与60x+1000 的大小了.解法一:设该单位参加旅游人数为x.
那么选甲旅行社,应付费用80x 元;
选乙旅行社,应付(60x+1000)元
记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
解:观察图象,可知:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
解法二:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50. 所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;解法三:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
它与x轴交点为(50,0) 由图可知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2. 某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费
为0.2元/min;
B方案: 零月租费,通话费为0.3元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出那
种付费方式合算?做一做(2)这两个函数的图象如下:t(min)y = 15+0.2ty = 0.5t观察图象,可知:
当通话时间为150min时,选择A或B方案费用一样;
当通话时间少于150min时,选择A方案费合算;
当通话时间多于150min时,选择B方案合算. 1.小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )A.小亮骑自行车的平均速度是12km/h
B.小明比小亮提前0.5小时到达滨湖湿地公园
C.小明在距学校12km处追上小亮
D.9:30小明与小亮相距4km当堂练习解:A.根据函数图象小亮去滨湖湿地公园所用时间为10﹣8=2小时,
∴小亮骑自行车的平均速度为:24÷2=12(km/h),故正确;
B.由图象可得,小明到滨湖湿地公园对应的时间t=9.5,小亮到滨湖湿地公园对应的时间t=10,10﹣9.5=0.5(小时),
∴小明比小亮提前0.5小时到达滨湖湿地公园,故正确;
C.由图象可知,当t=9时,小明追上小亮,此时小亮离开学校的时间为9﹣8=1小时,
∴小亮走的路程为:1×12=12km,
∴小明在距学校12km出追上小亮,故正确;
D.由图象可知,当t=9.5时,小明的路程为24km,小亮的路程为12×(9.5﹣8)=18km,此时小明与小亮相距24﹣18=6km,故错误;故选D.2.如图所示,l1反映了某公司产品的销售成本与销售量的关系, l2反映了此公司产品的销售收入与销售量的关系.根据图象填空:
Ox(吨)y(元)100020003000400050001234567l1l2(1)l1对应的表达是 ,l2对应的表达式是 ;
(2)当销售量为2吨时, 销售收入= 元,销售成本
= 元;
(3)当销售量为6吨时,销售收入= 元,销售成本
= 元;
(4)当销售量 吨时,销售收入等于销售成本;
(5)当销售量 吨时,该公司盈利(收入大于成本).当销售 吨时,该公司亏损(收入小于成本).y=500x+2000y=1000x3000等于4大于4小于46000500020003.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧
前的高度分别是 ,
从点燃到燃尽所用的时间
分别是 . 30厘米、25厘米 2时、2.5时(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?
在什么时间段内,甲蜡烛比乙蜡烛高?
在什么时间段内,甲蜡烛比乙蜡烛低?
y甲=-15x+30y乙=-10x+25x=1x>1x<1课堂小结两个一次函数的综合应用方案选择问题实际生活中的问题谢谢!
一次函数21.4 一次函数的应用
第2课时冀教版数学八年级下册1.会根据问题情境的数量关系建立相应的一次函数表达式.
(重点)
2.能利用两个一次函数解决实际问题.(难点)学习目标问题引入老师为了教学,需要在家上网查资料.电信公司提供了两种上网收费方式:
方式 1 :按上网时间以每小时 1 元计费;
方式 2 :月租费 20 元,再按上网时间以每小时 0.6 元计费.
请同学们帮老师选择:
以何种方式上网更合算?典例精析由于小红比小明晚出发2 h,因此小红所用时间为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3. (1)分别写出y1 ,y2与x之间的函数表达式;过点(0,40)作射线l 与x 轴平行,它先与射线
y2 = 40(x - 2)相交,这表明小红先到达乙地. (2)在同一个直角坐标系中,画出这两个函数的图象,
并指出谁先到达乙地.甲骑自行车以10千米每小时的速度沿公路行驶,出发3小时后,乙骑摩托车从同一地点出发沿公路与甲同向行驶,速度为25千米每小时.设甲离开出发地的时间为x小时.(2)写出乙离开出发地的路程y与x之间的函数关系式,并指出自变量x的取值范围;y=10x(x≥0)y=25x-75(x≥3)做一做(1)写出甲离开出发地的路程y与x之间的函数关系式,并指出自变量x的取值范围;y/千米0x/小时532110504030204甲y=10x乙y=25x-75由图可知,交点坐标是(5,50),即甲出发5小时后被乙追上,此时,两人距离出发地50千米(3)在同一直角坐标系中,画出(1)(2)中函数的图像,并结合实际问题,解释图像中交点的意义.例2 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少? 分析:假设该单位参加旅游人数为x,按甲旅行社的优惠条件,应付费用80x 元;按乙旅行社的优惠条件,应付费用(60x+1000)元.问题变为比较80x 与60x+1000 的大小了.解法一:设该单位参加旅游人数为x.
那么选甲旅行社,应付费用80x 元;
选乙旅行社,应付(60x+1000)元
记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
解:观察图象,可知:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
解法二:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50. 所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;解法三:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
它与x轴交点为(50,0) 由图可知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2. 某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费
为0.2元/min;
B方案: 零月租费,通话费为0.3元/min.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(min)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出那
种付费方式合算?做一做(2)这两个函数的图象如下:t(min)y = 15+0.2ty = 0.5t观察图象,可知:
当通话时间为150min时,选择A或B方案费用一样;
当通话时间少于150min时,选择A方案费合算;
当通话时间多于150min时,选择B方案合算. 1.小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )A.小亮骑自行车的平均速度是12km/h
B.小明比小亮提前0.5小时到达滨湖湿地公园
C.小明在距学校12km处追上小亮
D.9:30小明与小亮相距4km当堂练习解:A.根据函数图象小亮去滨湖湿地公园所用时间为10﹣8=2小时,
∴小亮骑自行车的平均速度为:24÷2=12(km/h),故正确;
B.由图象可得,小明到滨湖湿地公园对应的时间t=9.5,小亮到滨湖湿地公园对应的时间t=10,10﹣9.5=0.5(小时),
∴小明比小亮提前0.5小时到达滨湖湿地公园,故正确;
C.由图象可知,当t=9时,小明追上小亮,此时小亮离开学校的时间为9﹣8=1小时,
∴小亮走的路程为:1×12=12km,
∴小明在距学校12km出追上小亮,故正确;
D.由图象可知,当t=9.5时,小明的路程为24km,小亮的路程为12×(9.5﹣8)=18km,此时小明与小亮相距24﹣18=6km,故错误;故选D.2.如图所示,l1反映了某公司产品的销售成本与销售量的关系, l2反映了此公司产品的销售收入与销售量的关系.根据图象填空:
Ox(吨)y(元)100020003000400050001234567l1l2(1)l1对应的表达是 ,l2对应的表达式是 ;
(2)当销售量为2吨时, 销售收入= 元,销售成本
= 元;
(3)当销售量为6吨时,销售收入= 元,销售成本
= 元;
(4)当销售量 吨时,销售收入等于销售成本;
(5)当销售量 吨时,该公司盈利(收入大于成本).当销售 吨时,该公司亏损(收入小于成本).y=500x+2000y=1000x3000等于4大于4小于46000500020003.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧
前的高度分别是 ,
从点燃到燃尽所用的时间
分别是 . 30厘米、25厘米 2时、2.5时(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?
在什么时间段内,甲蜡烛比乙蜡烛高?
在什么时间段内,甲蜡烛比乙蜡烛低?
y甲=-15x+30y乙=-10x+25x=1x>1x<1课堂小结两个一次函数的综合应用方案选择问题实际生活中的问题谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
