冀教版数学八年级下册22.2 平行四边形的判定 第1课时 课件(18张ppt)
文档属性
| 名称 | 冀教版数学八年级下册22.2 平行四边形的判定 第1课时 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 22:43:33 | ||
图片预览





文档简介
课件18张PPT。第二十二章
四边形22.2 平行四边形的判定
第1课时冀教版数学八年级下册1.运用类比的方法,探索平行四边形的判定方法.
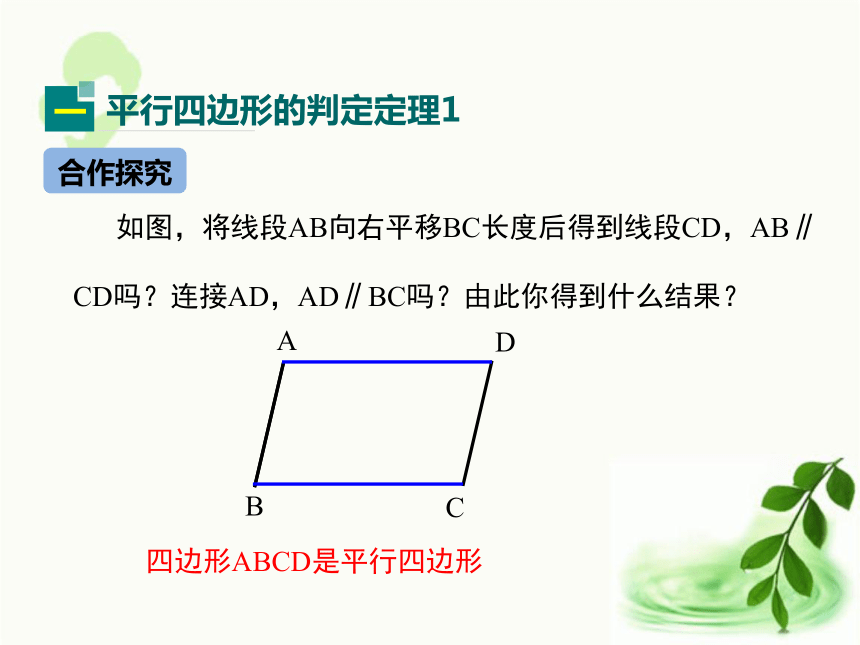
2.理解平行四边形的判定方法,并会简单运用.(重难点)学习目标 定义:有两组对边分别平行的四边形叫做平行四边形.平行四边形的对边相等,对角相等平行四边形的对角线互相平分.既是平行四边形的性质也是平行四边形的判定. 性质:复习引入 平行四边形定义是什么?它有哪些性质?合作探究BA 如图,将线段AB向右平移BC长度后得到线段CD,AB∥
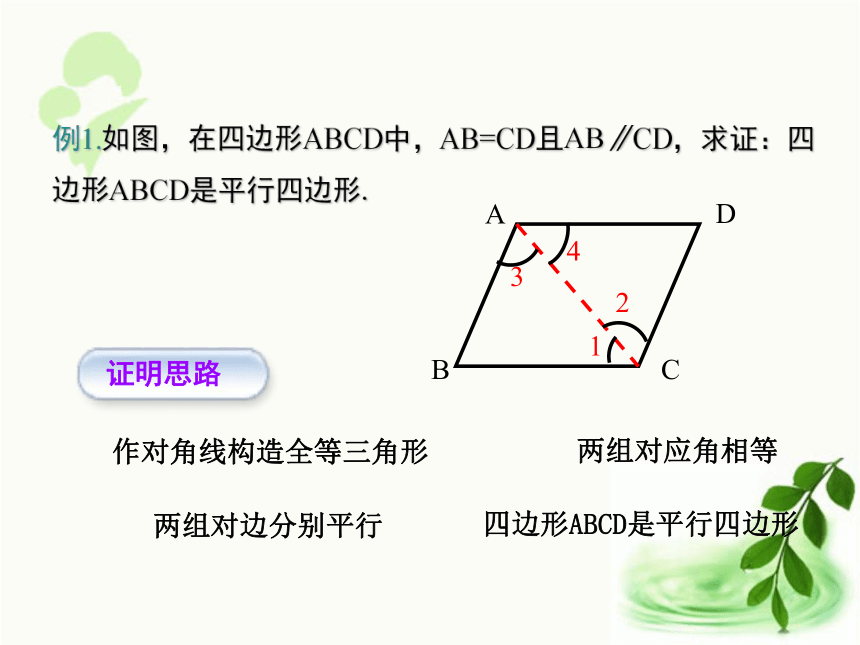
CD吗?连接AD,AD∥BC吗?由此你得到什么结果?DC四边形ABCD是平行四边形作对角线构造全等三角形两组对应角相等两组对边分别平行四边形ABCD是平行四边形例1.如图,在四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.证明:连结AC,
∵AB∥CD, ∴∠2=∠3
在△ABC和△CDA中,AB=CD (已知)AC=AC(公共边)∠3=∠2∴△ABC≌△CDA(SAS)∴ ∠1=∠4.∴AD∥ BC.
又AB∥ CD , ∴四边形ABCD是平行四边形.一组对边平行且相等的四边形是平行四边形.知识要点平行四边形的判定定理1:如等腰梯形 满足下列条件的四边形ABCD是不是平行四边形,若是,在括号内打“√”,若不是,则打“×”.√√√×(1)AB=CD,AB∥CD ( )
(2)AB ∥ CD,AD ∥ BC ( )
(3)AB ∥ CD,AD=BC ( )
(4)∠A+∠B=180°,AD=BC ( )练一练例2. 已知:如图,E,F分别是平行四边形ABCD 的边AD,BC的中点.求证:BE=DF.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵E,F分别是AD,BC的中点,∴ED=1/2AD,BF==1/2AD,即ED=BF.∴四边形EBFD是平行四边形∴BE=DF又ED∥BF,如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形. 证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线
∴∠B=∠D,AB=CD,
∠BAE=∠DCF= ∠DAB= ∠BCD ∴△ABE≌△CDF(ASA)
∴BE=DF,∴AF=CE .
又∵AF∥CE
∴四边形AFCE是平行四边形.如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出这些垂线段的长度.经过测量,我们发现这些垂线段的长度都相等.这种现象说明了平行线的又一个性质:平行线之间的距离处处相等.合作探究尝试证明这个结论.例3 如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .分析:利用平行线之间的距离处处相等.解:设AE与BD之间的距离为h,则S△ABD= ·BD·h=16,则h=4,
所以S △ACE= ·AE·h= ×5 ×4=10.10h证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.1.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.当堂练习2.已知:如图,AD∥BC,且AB=CD=5,AC=4,BC=3;
求证:AB∥CD.温馨提示:可利用勾股定理及其逆定理解题证明:∵在△ABC中,AB=5,AC=4,BC=3
∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°
∵ AD∥BC
∴∠DAC=∠ACB=90°
∵CD=5, AC=4,∴AD=3
∴AD∥BC 且AD=BC
∴四边形ABCD是平行四边形
∴ AB∥CD.3.(1)在□ABCD中,∠A=150°,AB=8cm,BC=10cm,则S □ABCD= .提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.40cm2(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .20cm2提示:△PBC与□ABCD是同底等高.平行四边形的判定定理1课堂小结一组对边平行且相等的四边形是平行四边形平行四边形的判定定理1平行线间的距离处处相等谢谢!
四边形22.2 平行四边形的判定
第1课时冀教版数学八年级下册1.运用类比的方法,探索平行四边形的判定方法.
2.理解平行四边形的判定方法,并会简单运用.(重难点)学习目标 定义:有两组对边分别平行的四边形叫做平行四边形.平行四边形的对边相等,对角相等平行四边形的对角线互相平分.既是平行四边形的性质也是平行四边形的判定. 性质:复习引入 平行四边形定义是什么?它有哪些性质?合作探究BA 如图,将线段AB向右平移BC长度后得到线段CD,AB∥
CD吗?连接AD,AD∥BC吗?由此你得到什么结果?DC四边形ABCD是平行四边形作对角线构造全等三角形两组对应角相等两组对边分别平行四边形ABCD是平行四边形例1.如图,在四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.证明:连结AC,
∵AB∥CD, ∴∠2=∠3
在△ABC和△CDA中,AB=CD (已知)AC=AC(公共边)∠3=∠2∴△ABC≌△CDA(SAS)∴ ∠1=∠4.∴AD∥ BC.
又AB∥ CD , ∴四边形ABCD是平行四边形.一组对边平行且相等的四边形是平行四边形.知识要点平行四边形的判定定理1:如等腰梯形 满足下列条件的四边形ABCD是不是平行四边形,若是,在括号内打“√”,若不是,则打“×”.√√√×(1)AB=CD,AB∥CD ( )
(2)AB ∥ CD,AD ∥ BC ( )
(3)AB ∥ CD,AD=BC ( )
(4)∠A+∠B=180°,AD=BC ( )练一练例2. 已知:如图,E,F分别是平行四边形ABCD 的边AD,BC的中点.求证:BE=DF.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵E,F分别是AD,BC的中点,∴ED=1/2AD,BF==1/2AD,即ED=BF.∴四边形EBFD是平行四边形∴BE=DF又ED∥BF,如图,在平行四边形ABCD中,已知AE、CF分别是∠DAB、∠BCD的角平分线,试证明四边形AFCE是平行四边形. 证明:∵在平行四边形ABCD中,
AE、CF分别是∠DAB、 ∠BCD的角平分线
∴∠B=∠D,AB=CD,
∠BAE=∠DCF= ∠DAB= ∠BCD ∴△ABE≌△CDF(ASA)
∴BE=DF,∴AF=CE .
又∵AF∥CE
∴四边形AFCE是平行四边形.如图,在方格纸上画两条互相平行的直线,在其中一条直线上任取若干点,过这些点作另一条直线的垂线,用刻度尺量出这些垂线段的长度.经过测量,我们发现这些垂线段的长度都相等.这种现象说明了平行线的又一个性质:平行线之间的距离处处相等.合作探究尝试证明这个结论.例3 如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .分析:利用平行线之间的距离处处相等.解:设AE与BD之间的距离为h,则S△ABD= ·BD·h=16,则h=4,
所以S △ACE= ·AE·h= ×5 ×4=10.10h证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.1.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.当堂练习2.已知:如图,AD∥BC,且AB=CD=5,AC=4,BC=3;
求证:AB∥CD.温馨提示:可利用勾股定理及其逆定理解题证明:∵在△ABC中,AB=5,AC=4,BC=3
∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°
∵ AD∥BC
∴∠DAC=∠ACB=90°
∵CD=5, AC=4,∴AD=3
∴AD∥BC 且AD=BC
∴四边形ABCD是平行四边形
∴ AB∥CD.3.(1)在□ABCD中,∠A=150°,AB=8cm,BC=10cm,则S □ABCD= .提示:过点A作AE⊥BC于E,然后利用勾股定理求出AE的值.40cm2(2)若点P是□ABCD上AD上任意一点,那么△PBC的面积是 .20cm2提示:△PBC与□ABCD是同底等高.平行四边形的判定定理1课堂小结一组对边平行且相等的四边形是平行四边形平行四边形的判定定理1平行线间的距离处处相等谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
