冀教版数学八年级下册22.3 三角形的中位线 课件(18张ppt)
文档属性
| 名称 | 冀教版数学八年级下册22.3 三角形的中位线 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 00:00:00 | ||
图片预览






文档简介
课件18张PPT。第二十二章
四边形22.3 三角形的中位线冀教版数学八年级下册1.理解三角形中位线的概念,掌握三角形的中位线定理.(重点)
2.能利用三角形的中位线定理解决有关证明和计算问题.
(重点)学习目标复习引入 在三角形中,连结一个 和它的 的
叫做三角形的中线. 它就是我们这节课要学习的三角形的中位线.顶点对边中点线段观察与思考2.一个三角形有几条中位线?3.三角形的中位线与中线有什么区别?答:三条.答:中位线是连接三角形两边中点的线段. 中线是连结一个顶点和它的对边中点的线段.定义:连接三角形两边中点的线段叫做
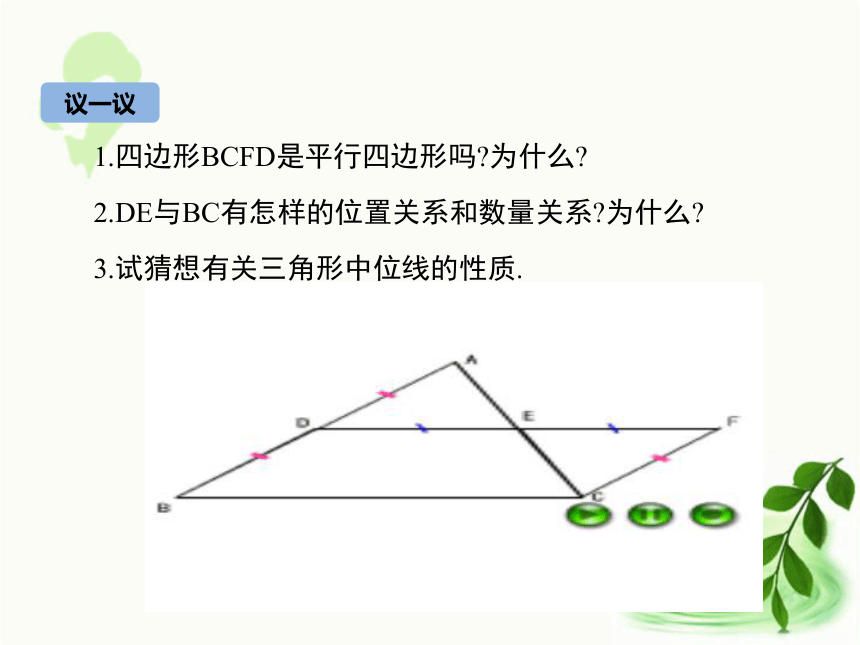
三角形的中位线.1.剪一个三角形,记为△ABC;2.分别取AB 、AC的中点D 、E,连结DE;3.沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180度,得四边形BCFD.怎样将一张三角形的纸片剪成两部分,使分成的两部分能拼成一个平行四边形?动手操作议一议1.四边形BCFD是平行四边形吗?为什么?2.DE与BC有怎样的位置关系和数量关系?为什么?3.试猜想有关三角形中位线的性质.BC试一试三角形中位线平行于第三边,并且等于它的一半.知识要点三角形的中位线定理:三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半.应用时要具体分析,需要哪一个就用哪一个.练一练己知:如图, E、F分别为AB、AC的中点.
(1)∵ E、F分别为AB、AC的中点.
∴ EF∥BC(根据? ???? ? ???? )
(2)若BC =10cm,
则EF = cm;
(3)若EF =6cm,
则BC = cm.ABCEF三角形中位线定理512求证:四边形EFGH是平行四边形.例1.如图,在四边形ABCD中, E,F,G,H分别为各边的中点.分析:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.典例精析证明:连接AC.∵E,F,G,H分别为各边的中点,∴ EF∥HG, EF=HG.∴EF∥AC,HG∥AC,∴四边形EFGH是平行四边形.结论:顺次连结四边形四条边的中点,所得的四边形是平行四边形.例2.如图,在四边形ABCD中,AD=BC,E,F分别是边AB,CD的中点,G为对角线BD的中点.
求证:△EFG是等腰三角形.例3.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.解:取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴在直角△EGF中,由用勾股定理,得∴EG∥AC,FG∥BD,G当堂练习1.已知:如图,点 D、E、F 分别是 △ABC 的三边
AB、BC、AC 的中点.
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
5015ABCDFE2.已知:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,有通过学习方法估测出了A,B两地之间的距离:先在AB外选一点C,然后找到AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗?解:其中的道理是:
∵MN是△ABC的的中位线,
∴AB=2MN.3.如图,在四边形ABCD中,E,F,G,H分别是边AB,CD,AC,BD的中点.
求证:四边形EGFH是平行四边形.证明:∵四边形ABCD中,点E、F、G、H分别是AB、CD、AC、BD的中点,∴FG∥AD,HE∥AD,FH∥CB,GE∥BC,
∴GE∥FH,GF∥EH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形; 课堂小结三角形的中位线三角形中位线平行于第三边,并且等于它的一半三角形的中位线定理三角形的中位线定理的应用谢谢!
四边形22.3 三角形的中位线冀教版数学八年级下册1.理解三角形中位线的概念,掌握三角形的中位线定理.(重点)
2.能利用三角形的中位线定理解决有关证明和计算问题.
(重点)学习目标复习引入 在三角形中,连结一个 和它的 的
叫做三角形的中线. 它就是我们这节课要学习的三角形的中位线.顶点对边中点线段观察与思考2.一个三角形有几条中位线?3.三角形的中位线与中线有什么区别?答:三条.答:中位线是连接三角形两边中点的线段. 中线是连结一个顶点和它的对边中点的线段.定义:连接三角形两边中点的线段叫做
三角形的中位线.1.剪一个三角形,记为△ABC;2.分别取AB 、AC的中点D 、E,连结DE;3.沿DE将△ABC剪成两部分,并将△ADE绕点E旋转180度,得四边形BCFD.怎样将一张三角形的纸片剪成两部分,使分成的两部分能拼成一个平行四边形?动手操作议一议1.四边形BCFD是平行四边形吗?为什么?2.DE与BC有怎样的位置关系和数量关系?为什么?3.试猜想有关三角形中位线的性质.BC试一试三角形中位线平行于第三边,并且等于它的一半.知识要点三角形的中位线定理:三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半.应用时要具体分析,需要哪一个就用哪一个.练一练己知:如图, E、F分别为AB、AC的中点.
(1)∵ E、F分别为AB、AC的中点.
∴ EF∥BC(根据? ???? ? ???? )
(2)若BC =10cm,
则EF = cm;
(3)若EF =6cm,
则BC = cm.ABCEF三角形中位线定理512求证:四边形EFGH是平行四边形.例1.如图,在四边形ABCD中, E,F,G,H分别为各边的中点.分析:将四边形ABCD分割为三角形,利用三角形的中位线可转化两组对边分别平行或一组对边平行且相等来证明.典例精析证明:连接AC.∵E,F,G,H分别为各边的中点,∴ EF∥HG, EF=HG.∴EF∥AC,HG∥AC,∴四边形EFGH是平行四边形.结论:顺次连结四边形四条边的中点,所得的四边形是平行四边形.例2.如图,在四边形ABCD中,AD=BC,E,F分别是边AB,CD的中点,G为对角线BD的中点.
求证:△EFG是等腰三角形.例3.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.解:取BC边的中点G,连接EG、FG.
∵E,F分别为AB,CD的中点,
∴EG是△ABC的中位线,FG是△BCD的中位线,又BD=12,AC=16,AC⊥BD,
∴EG=8,FG=6,EG⊥FG,
∴在直角△EGF中,由用勾股定理,得∴EG∥AC,FG∥BD,G当堂练习1.已知:如图,点 D、E、F 分别是 △ABC 的三边
AB、BC、AC 的中点.
(1)若∠ADF=50°,则∠B= °;
(2)已知三边AB、BC、AC分别为12、10、8,
则△ DEF的周长为 .
5015ABCDFE2.已知:如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,有通过学习方法估测出了A,B两地之间的距离:先在AB外选一点C,然后找到AC,BC的中点M,N,并测出MN的长,由此他就知道了A,B间的距离.你能说出其中的道理吗?解:其中的道理是:
∵MN是△ABC的的中位线,
∴AB=2MN.3.如图,在四边形ABCD中,E,F,G,H分别是边AB,CD,AC,BD的中点.
求证:四边形EGFH是平行四边形.证明:∵四边形ABCD中,点E、F、G、H分别是AB、CD、AC、BD的中点,∴FG∥AD,HE∥AD,FH∥CB,GE∥BC,
∴GE∥FH,GF∥EH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形; 课堂小结三角形的中位线三角形中位线平行于第三边,并且等于它的一半三角形的中位线定理三角形的中位线定理的应用谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
