冀教版数学八年级下册22.4 矩形 第1课时 课件(23张ppt)
文档属性
| 名称 | 冀教版数学八年级下册22.4 矩形 第1课时 课件(23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 22:50:24 | ||
图片预览





文档简介
课件23张PPT。第二十二章
四边形22.4 矩形
第1课时冀教版数学八年级下册1.了解矩形的概念及其与平行四边形的关系;
2.探索并证明矩形的性质定理.(重点)
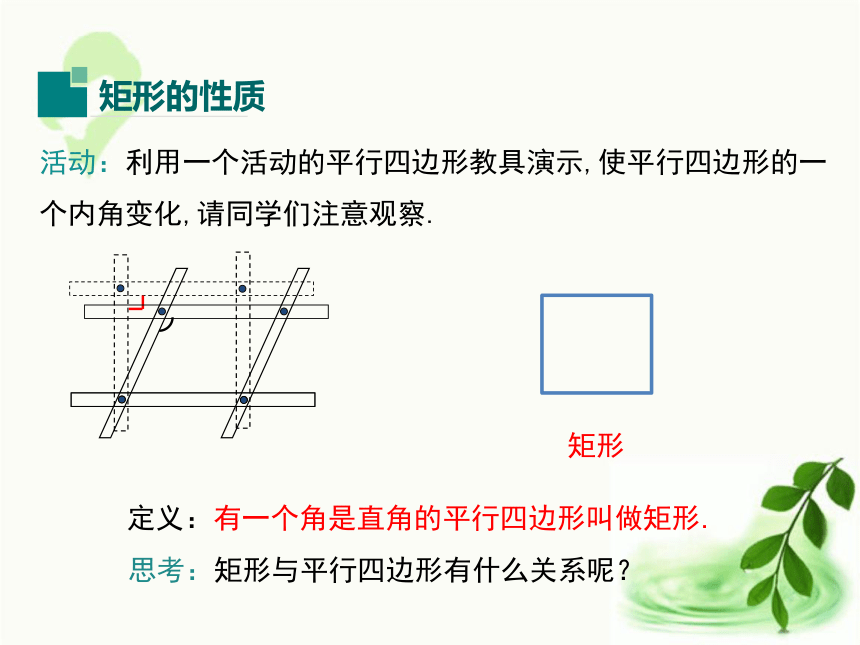
3.应用矩形的性质定理解决相关问题.(难点)学习目标活动:观察下面的图形,它们都含有平行四边形,请把它们全部找出来.问题:上面的平行四边形有什么共同的特征?图片引入活动:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.定义:有一个角是直角的平行四边形叫做矩形.矩形思考:矩形与平行四边形有什么关系呢?活动探究:
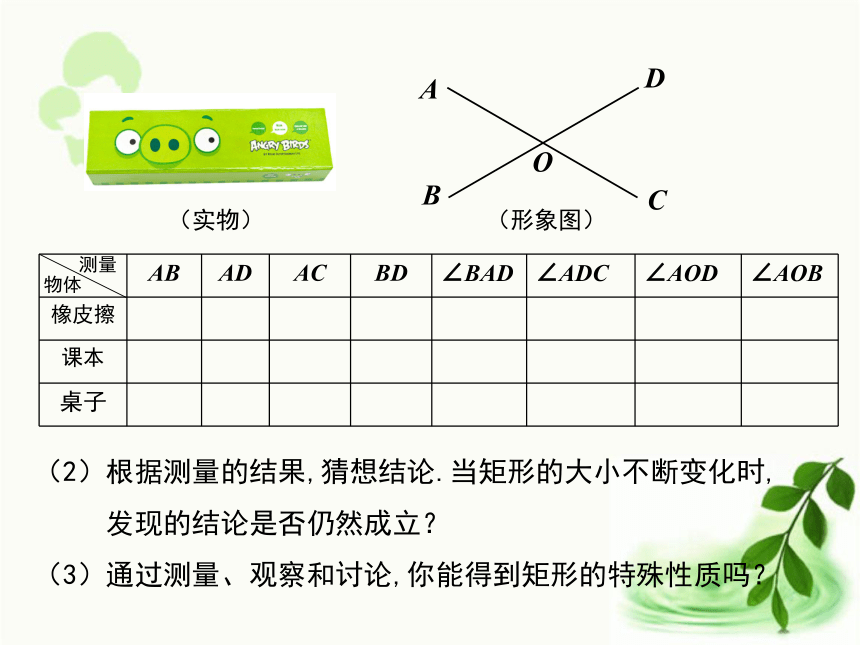
准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.
(1)请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.(2)根据测量的结果,猜想结论.当矩形的大小不断变化时,
发现的结论是否仍然成立?
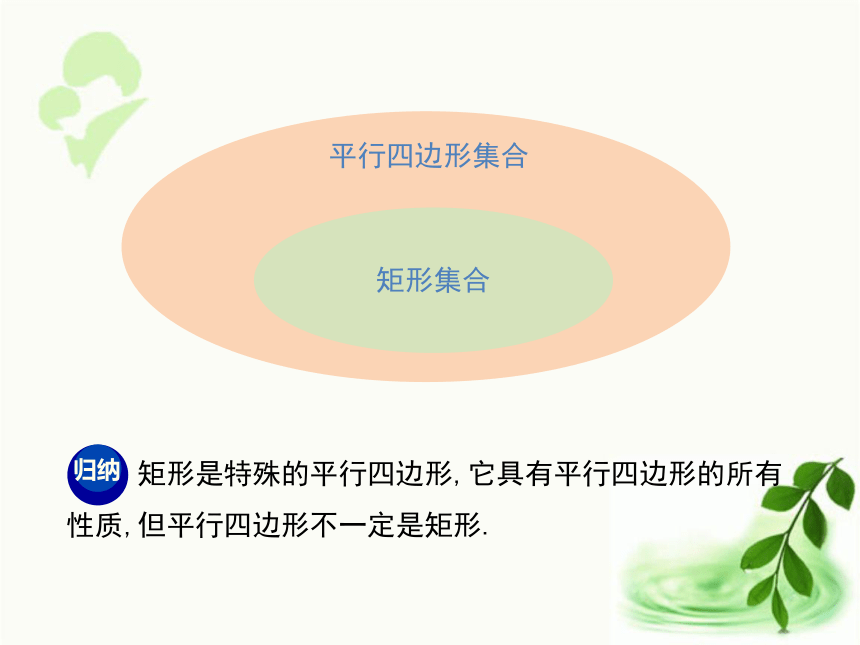
(3)通过测量、观察和讨论,你能得到矩形的特殊性质吗?ABCDO物体测量(实物)(形象图) 矩形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是矩形.矩形集合平行四边形集合填一填 根据上面探究出来结论填在下面横线上.
角: .
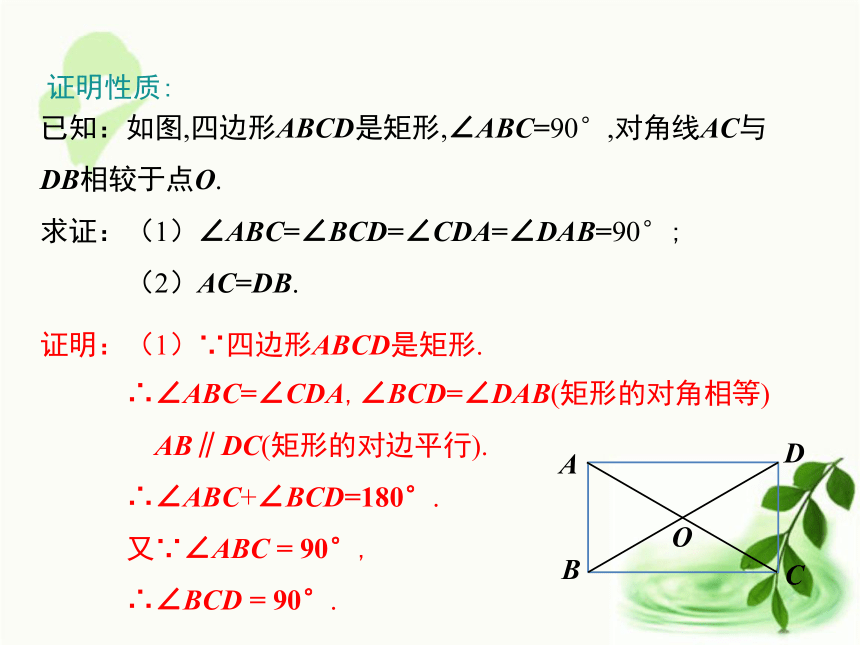
对角线: .ABCD四个角为90°相等O证明:(1)∵四边形ABCD是矩形.
∴∠ABC=∠CDA,∠BCD=∠DAB(矩形的对角相等)
AB∥DC(矩形的对边平行).
∴∠ABC+∠BCD=180°.
又∵∠ABC = 90°,
∴∠BCD = 90°.证明性质:已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.
求证:(1)∠ABC=∠BCD=∠CDA=∠DAB=90°;
(2)AC=DB.ABCDO∴∠ABC=∠BCD=∠CDA=∠DAB =90°.
(2)∵四边形ABCD是矩形,
∴AB=DC(矩形的对边相等).
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
∴AC=DB. 1.矩形的四个内角都是直角.
2.矩形的对角线相等.ABCDO做一做:请同学们拿出准备好的矩形纸片,折一折,观察并思考.??
(1)矩形是不是中心对称图形? 如果是,那么对称中心是什么?
(2)矩形是不是轴对称图形?如果是,那么对称轴有几条?矩形的性质(除中心对称外)
对称性: .
对称轴: .
轴对称图形2条归纳结论 矩形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.对称性:是轴对称图形.
角:四条内角都是90°.
对角线:相等. 角:对角相等.
边:对边平行且相等.
对角线:相互平分.矩形的特殊性质平行四边形的性质例1:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形对角线相互平分)
∴OA = OD.ABCDO典例精析∵∠AOD=120°,
∴∠ODA=∠OAD= (180°- 120°)=30°.
又∵∠DAB=90° ,
(矩形的四个角都是直角)
∴BD = 2AB = 2 ×2.5 = 5.提示:∠AOD=120° → ∠AOB=60°→ OA=OB=AB → AC=2OA
=2×2.5=5.你还有其他解法吗?例2:如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.
求证:DF=DC.ABCDEF证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC, ∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.又∵DE= DE,
∴△DFE≌△DCE,
∴DF=DC.3.已知:如图,矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,则矩形对角线的长为 cm当堂练习
2.矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80D81.矩形具有而平行四边形不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等B4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE,
(2)若∠DBC=30° , BO=4 ,求四边形ABED的面积.ABCDOE(1)证明:∵四边形ABCD是矩形.
∴AC= BD,AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.(2)解:∵在矩形ABCD中,BO=4,
∴BD = 2BO =2×4=8.
∵∠DBC=30°,
∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,
BC=
∴四边形ABED的面积= (4+8)× = .ABCDOE5.如图,在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
(1)如果FE⊥AE,求证FE=AE.
(2)如果FE=AE ,你能证明FE⊥AE吗?证明:(1)∵BE平分∠ABC,∴∠ABE=∠CBE, ∵矩形对边AB∥CD, ∴∠ABE=∠BEC, ∴∠CBE=∠BEC, ∴BC=CE,
∵矩形ABCD的对边AD=BC, ∴AD=CE, ∵FE⊥AE, ∴∠AED+∠CEF=90°, ∵∠DAE+∠AED=90°, ∴∠DAE=∠CEF,
在△ADE和△ECF中,∴△ADE≌△ECF(ASA), ∴FE=AE(2)同(1)可证AD=CE,
在Rt△ADE和Rt△ECF中,∴Rt△ADE≌Rt△ECF(HL), ∴∠DAE=∠CEF, ∴∠AED+∠CEF=∠AED+∠DAE=90°, ∴∠AEF=180°-(∠AED+∠CEF)=180°-90°=90°, ∴FE⊥AE.课堂小结矩形的性质具有平行四边行的一切性质矩形的性质定理四个内角都是直角,两条对角线相等轴对称图形有两条对称轴谢谢!
四边形22.4 矩形
第1课时冀教版数学八年级下册1.了解矩形的概念及其与平行四边形的关系;
2.探索并证明矩形的性质定理.(重点)
3.应用矩形的性质定理解决相关问题.(难点)学习目标活动:观察下面的图形,它们都含有平行四边形,请把它们全部找出来.问题:上面的平行四边形有什么共同的特征?图片引入活动:利用一个活动的平行四边形教具演示,使平行四边形的一个内角变化,请同学们注意观察.定义:有一个角是直角的平行四边形叫做矩形.矩形思考:矩形与平行四边形有什么关系呢?活动探究:
准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.
(1)请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.(2)根据测量的结果,猜想结论.当矩形的大小不断变化时,
发现的结论是否仍然成立?
(3)通过测量、观察和讨论,你能得到矩形的特殊性质吗?ABCDO物体测量(实物)(形象图) 矩形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是矩形.矩形集合平行四边形集合填一填 根据上面探究出来结论填在下面横线上.
角: .
对角线: .ABCD四个角为90°相等O证明:(1)∵四边形ABCD是矩形.
∴∠ABC=∠CDA,∠BCD=∠DAB(矩形的对角相等)
AB∥DC(矩形的对边平行).
∴∠ABC+∠BCD=180°.
又∵∠ABC = 90°,
∴∠BCD = 90°.证明性质:已知:如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.
求证:(1)∠ABC=∠BCD=∠CDA=∠DAB=90°;
(2)AC=DB.ABCDO∴∠ABC=∠BCD=∠CDA=∠DAB =90°.
(2)∵四边形ABCD是矩形,
∴AB=DC(矩形的对边相等).
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
∴AC=DB. 1.矩形的四个内角都是直角.
2.矩形的对角线相等.ABCDO做一做:请同学们拿出准备好的矩形纸片,折一折,观察并思考.??
(1)矩形是不是中心对称图形? 如果是,那么对称中心是什么?
(2)矩形是不是轴对称图形?如果是,那么对称轴有几条?矩形的性质(除中心对称外)
对称性: .
对称轴: .
轴对称图形2条归纳结论 矩形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.对称性:是轴对称图形.
角:四条内角都是90°.
对角线:相等. 角:对角相等.
边:对边平行且相等.
对角线:相互平分.矩形的特殊性质平行四边形的性质例1:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形对角线相互平分)
∴OA = OD.ABCDO典例精析∵∠AOD=120°,
∴∠ODA=∠OAD= (180°- 120°)=30°.
又∵∠DAB=90° ,
(矩形的四个角都是直角)
∴BD = 2AB = 2 ×2.5 = 5.提示:∠AOD=120° → ∠AOB=60°→ OA=OB=AB → AC=2OA
=2×2.5=5.你还有其他解法吗?例2:如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.
求证:DF=DC.ABCDEF证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC, ∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.又∵DE= DE,
∴△DFE≌△DCE,
∴DF=DC.3.已知:如图,矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,则矩形对角线的长为 cm当堂练习
2.矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80D81.矩形具有而平行四边形不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等B4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE,
(2)若∠DBC=30° , BO=4 ,求四边形ABED的面积.ABCDOE(1)证明:∵四边形ABCD是矩形.
∴AC= BD,AB∥CD.
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.(2)解:∵在矩形ABCD中,BO=4,
∴BD = 2BO =2×4=8.
∵∠DBC=30°,
∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,
BC=
∴四边形ABED的面积= (4+8)× = .ABCDOE5.如图,在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
(1)如果FE⊥AE,求证FE=AE.
(2)如果FE=AE ,你能证明FE⊥AE吗?证明:(1)∵BE平分∠ABC,∴∠ABE=∠CBE, ∵矩形对边AB∥CD, ∴∠ABE=∠BEC, ∴∠CBE=∠BEC, ∴BC=CE,
∵矩形ABCD的对边AD=BC, ∴AD=CE, ∵FE⊥AE, ∴∠AED+∠CEF=90°, ∵∠DAE+∠AED=90°, ∴∠DAE=∠CEF,
在△ADE和△ECF中,∴△ADE≌△ECF(ASA), ∴FE=AE(2)同(1)可证AD=CE,
在Rt△ADE和Rt△ECF中,∴Rt△ADE≌Rt△ECF(HL), ∴∠DAE=∠CEF, ∴∠AED+∠CEF=∠AED+∠DAE=90°, ∴∠AEF=180°-(∠AED+∠CEF)=180°-90°=90°, ∴FE⊥AE.课堂小结矩形的性质具有平行四边行的一切性质矩形的性质定理四个内角都是直角,两条对角线相等轴对称图形有两条对称轴谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
