冀教版数学八年级下册22.4 矩形 第2课时 课件(19张ppt)
文档属性
| 名称 | 冀教版数学八年级下册22.4 矩形 第2课时 课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 00:00:00 | ||
图片预览





文档简介
课件19张PPT。第二十二章
四边形22.4 矩形
第2课时冀教版数学八年级下册1.理解并掌握矩形的判定方法.(重点)
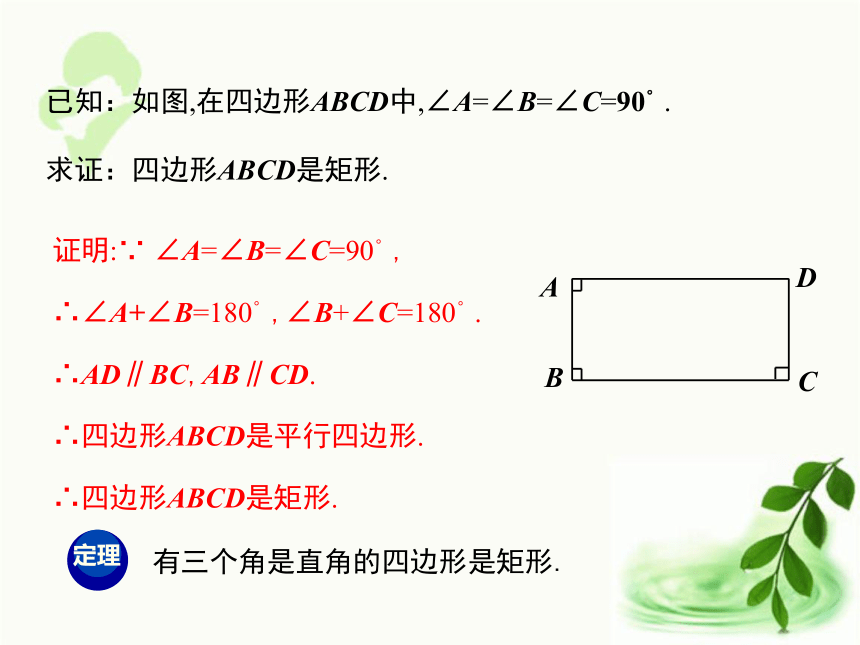
2.能应用矩形判定解决简单的证明题和计算题.(难点)学习目标问题引入 假如你是做窗框的师傅,你有什么方法检验你做的这个窗框是矩形?(直角尺等)矩形的定义:有一个角是直角的平行四边形是矩形.你还有其它的方法吗?活动1: 李芳同学通过画“边-直角、边-直角、边-直角、边”这样四步画出一个四边形.①②③④问题1:李芳觉得按照以上步骤可以得到一个矩形.你认为她的判断正确吗?如果正确,你能证明吗?已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
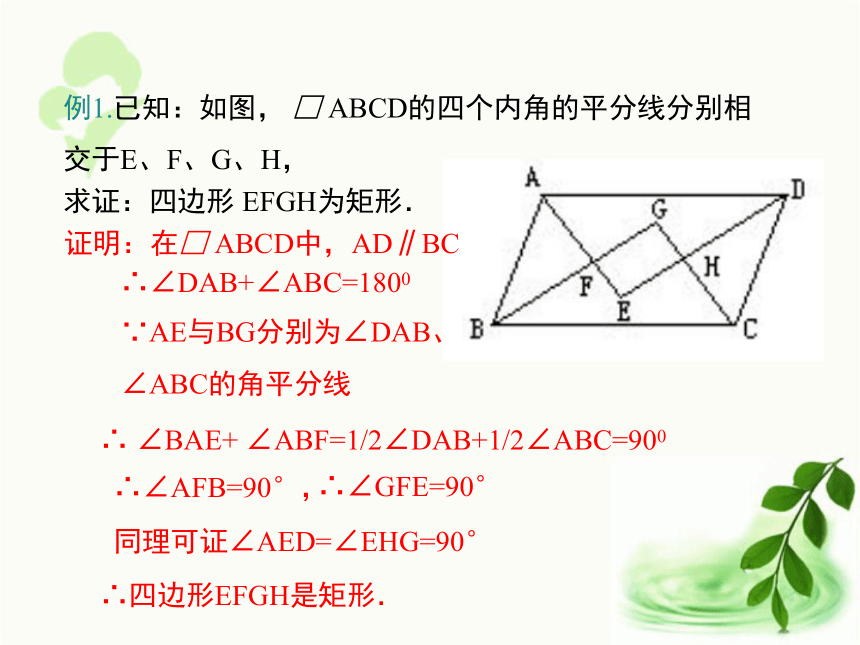
∴四边形ABCD是矩形. 有三个角是直角的四边形是矩形.例1.已知:如图, □?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.∴四边形EFGH是矩形.同理可证∠AED=∠EHG=90°证明:在□?ABCD中,AD∥BC∴∠DAB+∠ABC=1800∵AE与BG分别为∠DAB、
∠ABC的角平分线∴ ∠BAE+ ∠ABF=1/2∠DAB+1/2∠ABC=900∴∠AFB=90°,∴∠GFE=90°活动2: 利用一个活动的平行四边形教具演示,拉动一对不相邻的顶点时, 注意观察两条对角线的长度.问题2:我们会看到对角线会随着∠α变化而变化,当两条对角线长度相等时,平行四边形有什么特征?α已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.
求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义). 对角线相等的平行四边形是矩形. 例2.已知:如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.证明:∵四边形ABCD是矩形∴AC=BD(矩形的对角线相等)AO=BO=CO=DO(矩形的对角线互相平分)∵ AE=BF=CG=DH∴OE=OF=OG=OH∴四边形EFGH是平行四边形∵EO+OG=FO+OH即EG=FH
∴四边形EFGH是矩形.若变为:E、F、G、H分别是AO、BO、CO、DO的中点,你会吗?做一做已知□ABCD的对角线AC、BD交于O,△AOB是等边三角形,AB = 4cm,求这个平行四边形的面积.当堂练习1.下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(4)有三个角都相等的四边形是矩形;××××√√√√(8)一组对角互补的平行四边形是矩形;2.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、 ∠MCA、 ∠ ACN、∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定C3.如图 ABCD中, ∠1= ∠2中.此时四边形ABCD是矩形吗?为什么?12解:四边形ABCD是矩形.理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
又∵ ∠1= ∠2
∴AO=BO
∴AC=BD
∴四边形ABCD是矩形.4.△ABC中,点O是AC边上一动点,过O点作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
(1)试说明EO=OF.
(2)当点O运动到何处时,四边形AECF是矩形?并说明你的理由.MNBCDEOFA解:(1)∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;(2)当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.课堂小结有一个角是直角的平行四边形是矩形.定理2:对角线相等的平行四边形是矩形.定理1:有三个角是直角的四边形是矩形.运用定理进行计算和证明.矩形的判定定义定理谢谢!
四边形22.4 矩形
第2课时冀教版数学八年级下册1.理解并掌握矩形的判定方法.(重点)
2.能应用矩形判定解决简单的证明题和计算题.(难点)学习目标问题引入 假如你是做窗框的师傅,你有什么方法检验你做的这个窗框是矩形?(直角尺等)矩形的定义:有一个角是直角的平行四边形是矩形.你还有其它的方法吗?活动1: 李芳同学通过画“边-直角、边-直角、边-直角、边”这样四步画出一个四边形.①②③④问题1:李芳觉得按照以上步骤可以得到一个矩形.你认为她的判断正确吗?如果正确,你能证明吗?已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形. 有三个角是直角的四边形是矩形.例1.已知:如图, □?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形 EFGH为矩形.∴四边形EFGH是矩形.同理可证∠AED=∠EHG=90°证明:在□?ABCD中,AD∥BC∴∠DAB+∠ABC=1800∵AE与BG分别为∠DAB、
∠ABC的角平分线∴ ∠BAE+ ∠ABF=1/2∠DAB+1/2∠ABC=900∴∠AFB=90°,∴∠GFE=90°活动2: 利用一个活动的平行四边形教具演示,拉动一对不相邻的顶点时, 注意观察两条对角线的长度.问题2:我们会看到对角线会随着∠α变化而变化,当两条对角线长度相等时,平行四边形有什么特征?α已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.
求证:□ABCD是矩形.
证明:∵AB = DC,BC = CB,AC = DB,
∴ △ABC≌△DCB ,
∴∠ABC = ∠DCB.
∵AB∥CD,
∴∠ABC + ∠DCB = 180°,
∴ ∠ABC = 90°,
∴ □ ABCD是矩形(矩形的定义). 对角线相等的平行四边形是矩形. 例2.已知:如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.证明:∵四边形ABCD是矩形∴AC=BD(矩形的对角线相等)AO=BO=CO=DO(矩形的对角线互相平分)∵ AE=BF=CG=DH∴OE=OF=OG=OH∴四边形EFGH是平行四边形∵EO+OG=FO+OH即EG=FH
∴四边形EFGH是矩形.若变为:E、F、G、H分别是AO、BO、CO、DO的中点,你会吗?做一做已知□ABCD的对角线AC、BD交于O,△AOB是等边三角形,AB = 4cm,求这个平行四边形的面积.当堂练习1.下列各句判定矩形的说法是否正确?(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(4)有三个角都相等的四边形是矩形;××××√√√√(8)一组对角互补的平行四边形是矩形;2.如图,直线EF∥MN,PQ交EF、MN于A、C两点,AB、CB、CD、AD分别是∠EAC、 ∠MCA、 ∠ ACN、∠CAF的角平分线,则四边形ABCD是( )
A.菱形 B.平行四边形 C.矩形 D.不能确定C3.如图 ABCD中, ∠1= ∠2中.此时四边形ABCD是矩形吗?为什么?12解:四边形ABCD是矩形.理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,DO=BO.
又∵ ∠1= ∠2
∴AO=BO
∴AC=BD
∴四边形ABCD是矩形.4.△ABC中,点O是AC边上一动点,过O点作直线MN//BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,
(1)试说明EO=OF.
(2)当点O运动到何处时,四边形AECF是矩形?并说明你的理由.MNBCDEOFA解:(1)∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO;(2)当点O运动到AC的中点时,四边形AECF是矩形.
理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.课堂小结有一个角是直角的平行四边形是矩形.定理2:对角线相等的平行四边形是矩形.定理1:有三个角是直角的四边形是矩形.运用定理进行计算和证明.矩形的判定定义定理谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
