冀教版数学八年级下册22.5 菱形 第1课时 课件(20张ppt)
文档属性
| 名称 | 冀教版数学八年级下册22.5 菱形 第1课时 课件(20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-14 22:55:49 | ||
图片预览




文档简介
课件20张PPT。第二十二章
四边形22.5 菱形
第1课时冀教版数学八年级下册1.了解菱形的概念及其与平行四边形的关系;
2.探索并证明菱形的性质定理.(重点)
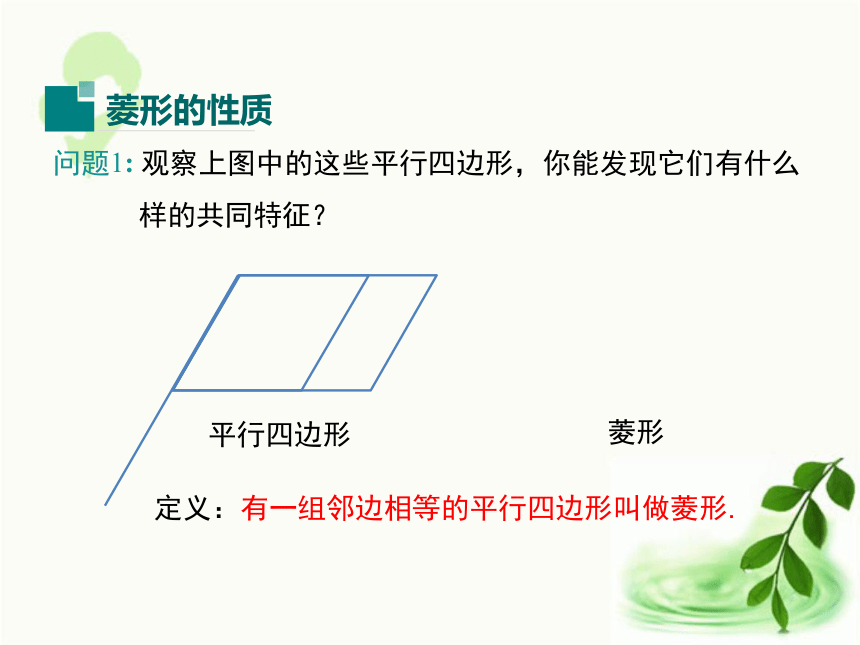
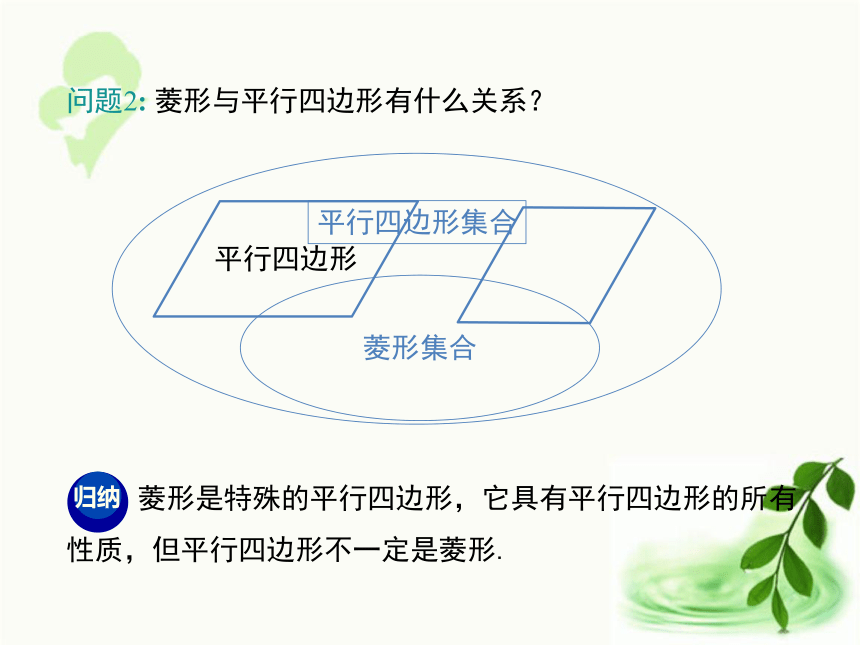
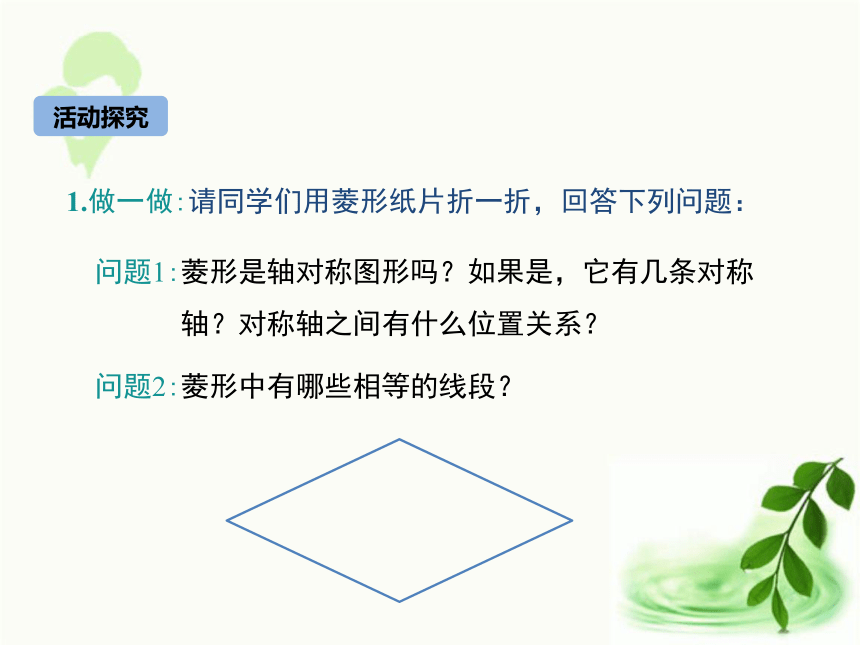
3.应用菱形的性质定理解决相关问题.(难点)学习目标图片引入下面的图形中有你熟悉的吗?问题1: 观察上图中的这些平行四边形,你能发现它们有什么 样的共同特征?平行四边形菱形定义:有一组邻边相等的平行四边形叫做菱形. 菱形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是菱形.问题2: 菱形与平行四边形有什么关系?平行四边形菱形集合平行四边形集合活动探究1.做一做:请同学们用菱形纸片折一折,回答下列问题:
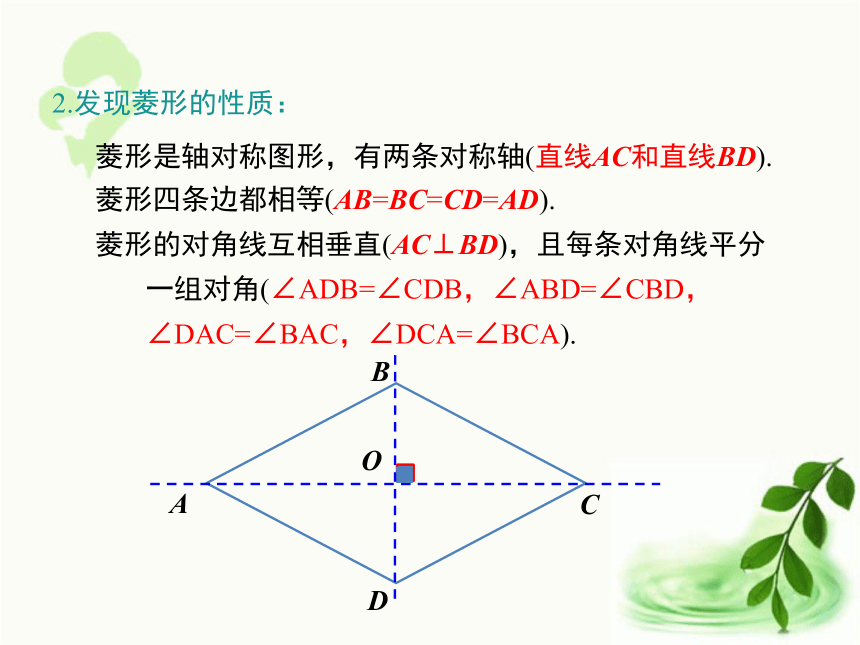
问题1:菱形是轴对称图形吗?如果是,它有几条对称 轴?对称轴之间有什么位置关系? 问题2:菱形中有哪些相等的线段?2.发现菱形的性质:
菱形是轴对称图形,有两条对称轴(直线AC和直线BD).
菱形四条边都相等(AB=BC=CD=AD).
菱形的对角线互相垂直(AC⊥BD),且每条对角线平分
一组对角(∠ADB=∠CDB,∠ABD=∠CBD,
∠DAC=∠BAC,∠DCA=∠BCA).
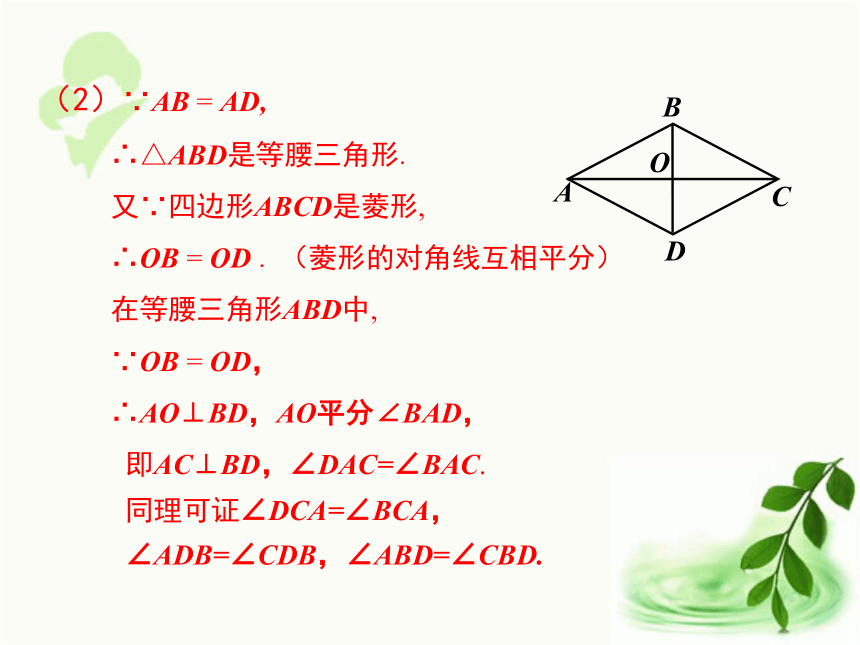
ABCOD已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
(3)∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD. 3.证明菱形性质:证明:(1)∵四边形ABCD是菱形,
∴AB = CD,AD = BC(菱形的对边相等).
又∵AB=AD;
∴AB = BC = CD =AD.(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD . (菱形的对角线互相平分)
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.4.归纳结论 菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.对称性:是轴对称图形.边:四条边都相等.
对角线:互相垂直,且每
条对角线平分一组对角. 角:对角相等.
边:对边平行且相等.
对角线:相互平分.菱形的特殊性质平行四边形的性质典例精析例1.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,
求证:EB=OA;分析:要证EB=OA,只需证它们所在的三角形全等,即△AOD≌△BEA.证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA, ∠ABC=∠ADC=2∠ADB
∴∠DAE=∠AEB? ∵AB=AE,∴∠ABC=∠AEB
∴∠ABC=∠DAE? ∵∠DAE=2∠BAE,∴∠BAE=∠ADB? 又∵AD=BA
∴△AOD≌△BEA
∴AO=BE 例2.如图,菱形ABCD的周长为16cm,∠ABC=120°,对角线AC、BD相交于点O,求对角线BD和AC的长.解:∵AB+BC+CD+AD=16cm,
∴AB=BC=CD=AD=4cm.
∵ BD平分∠ABC,∠ABC=120°,
∴∠ABD=60°
∴ △ABD是等边三角形.
∴ BD=AB = 4cm.
在Rt△AOB中,OB=2cm,
ABCDOABDCah(1)S = a·h.
(2)S = S△ABD+S△BCD
= AO·DB + CO·DB
= AC·DB. O菱形的面积计算公式:补充拓展菱形的面积对角线乘积的一半.当堂练习(1)菱形ABCD中,∠ABC=60°,则∠BAC=_______.60°(2)若菱形两条对角线长分别为6cm和8cm,则菱形的边长是_____.345cm(3)菱形的一个内角为120°,平分这个内角的对角线长为11cm,菱形的周长为______.
44cm1.填空(5)如图,在边长为6的菱形ABCD中,∠DAB=60 o ,E是AB的中点,F是AC上的动点,则EF+BF的最小值为______(4)菱形的面积为64平方厘米,两条对角线的比为1∶2 ,那么菱形的边长为_______.8厘米AEFDCBE'(1)菱形具有而一般平行四边形不具有的性质是( ) A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等(2)在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75° B.60° C.45° D.30°BC2.选择3.已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1)对角线AC的长度;
(2)菱形ABCD的面积.解:(1)∵四边形ABCD是菱形,∴∠AED=90°,(2)菱形ABCD的面积∴AC=2AE=2×12=24(cm).课堂小结菱形的性质菱形的性质有关计算1.四边相等
2.对角线互相垂直平分1.周长:边长的四倍
2.面积:两条对角线乘积的一半谢谢!
四边形22.5 菱形
第1课时冀教版数学八年级下册1.了解菱形的概念及其与平行四边形的关系;
2.探索并证明菱形的性质定理.(重点)
3.应用菱形的性质定理解决相关问题.(难点)学习目标图片引入下面的图形中有你熟悉的吗?问题1: 观察上图中的这些平行四边形,你能发现它们有什么 样的共同特征?平行四边形菱形定义:有一组邻边相等的平行四边形叫做菱形. 菱形是特殊的平行四边形,它具有平行四边形的所有性质,但平行四边形不一定是菱形.问题2: 菱形与平行四边形有什么关系?平行四边形菱形集合平行四边形集合活动探究1.做一做:请同学们用菱形纸片折一折,回答下列问题:
问题1:菱形是轴对称图形吗?如果是,它有几条对称 轴?对称轴之间有什么位置关系? 问题2:菱形中有哪些相等的线段?2.发现菱形的性质:
菱形是轴对称图形,有两条对称轴(直线AC和直线BD).
菱形四条边都相等(AB=BC=CD=AD).
菱形的对角线互相垂直(AC⊥BD),且每条对角线平分
一组对角(∠ADB=∠CDB,∠ABD=∠CBD,
∠DAC=∠BAC,∠DCA=∠BCA).
ABCOD已知:如图,在菱形ABCD中,AB=AD,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
(2)AC⊥BD;
(3)∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD. 3.证明菱形性质:证明:(1)∵四边形ABCD是菱形,
∴AB = CD,AD = BC(菱形的对边相等).
又∵AB=AD;
∴AB = BC = CD =AD.(2)∵AB = AD,
∴△ABD是等腰三角形.
又∵四边形ABCD是菱形,
∴OB = OD . (菱形的对角线互相平分)
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,∠ABD=∠CBD.4.归纳结论 菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.对称性:是轴对称图形.边:四条边都相等.
对角线:互相垂直,且每
条对角线平分一组对角. 角:对角相等.
边:对边平行且相等.
对角线:相互平分.菱形的特殊性质平行四边形的性质典例精析例1.如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,
求证:EB=OA;分析:要证EB=OA,只需证它们所在的三角形全等,即△AOD≌△BEA.证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA, ∠ABC=∠ADC=2∠ADB
∴∠DAE=∠AEB? ∵AB=AE,∴∠ABC=∠AEB
∴∠ABC=∠DAE? ∵∠DAE=2∠BAE,∴∠BAE=∠ADB? 又∵AD=BA
∴△AOD≌△BEA
∴AO=BE 例2.如图,菱形ABCD的周长为16cm,∠ABC=120°,对角线AC、BD相交于点O,求对角线BD和AC的长.解:∵AB+BC+CD+AD=16cm,
∴AB=BC=CD=AD=4cm.
∵ BD平分∠ABC,∠ABC=120°,
∴∠ABD=60°
∴ △ABD是等边三角形.
∴ BD=AB = 4cm.
在Rt△AOB中,OB=2cm,
ABCDOABDCah(1)S = a·h.
(2)S = S△ABD+S△BCD
= AO·DB + CO·DB
= AC·DB. O菱形的面积计算公式:补充拓展菱形的面积对角线乘积的一半.当堂练习(1)菱形ABCD中,∠ABC=60°,则∠BAC=_______.60°(2)若菱形两条对角线长分别为6cm和8cm,则菱形的边长是_____.345cm(3)菱形的一个内角为120°,平分这个内角的对角线长为11cm,菱形的周长为______.
44cm1.填空(5)如图,在边长为6的菱形ABCD中,∠DAB=60 o ,E是AB的中点,F是AC上的动点,则EF+BF的最小值为______(4)菱形的面积为64平方厘米,两条对角线的比为1∶2 ,那么菱形的边长为_______.8厘米AEFDCBE'(1)菱形具有而一般平行四边形不具有的性质是( ) A.对角相等 B.对边相等
C.对角线互相垂直 D.对角线相等(2)在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75° B.60° C.45° D.30°BC2.选择3.已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.求:(1)对角线AC的长度;
(2)菱形ABCD的面积.解:(1)∵四边形ABCD是菱形,∴∠AED=90°,(2)菱形ABCD的面积∴AC=2AE=2×12=24(cm).课堂小结菱形的性质菱形的性质有关计算1.四边相等
2.对角线互相垂直平分1.周长:边长的四倍
2.面积:两条对角线乘积的一半谢谢!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
