2020年苏科版七年级数学下册第七章平面图形的认识(二)尖子生特训题含答案
文档属性
| 名称 | 2020年苏科版七年级数学下册第七章平面图形的认识(二)尖子生特训题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 294.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 13:02:14 | ||
图片预览


文档简介
2020年苏科版七年级数学下册第七章平面图形的认识(二)尖子生特训题
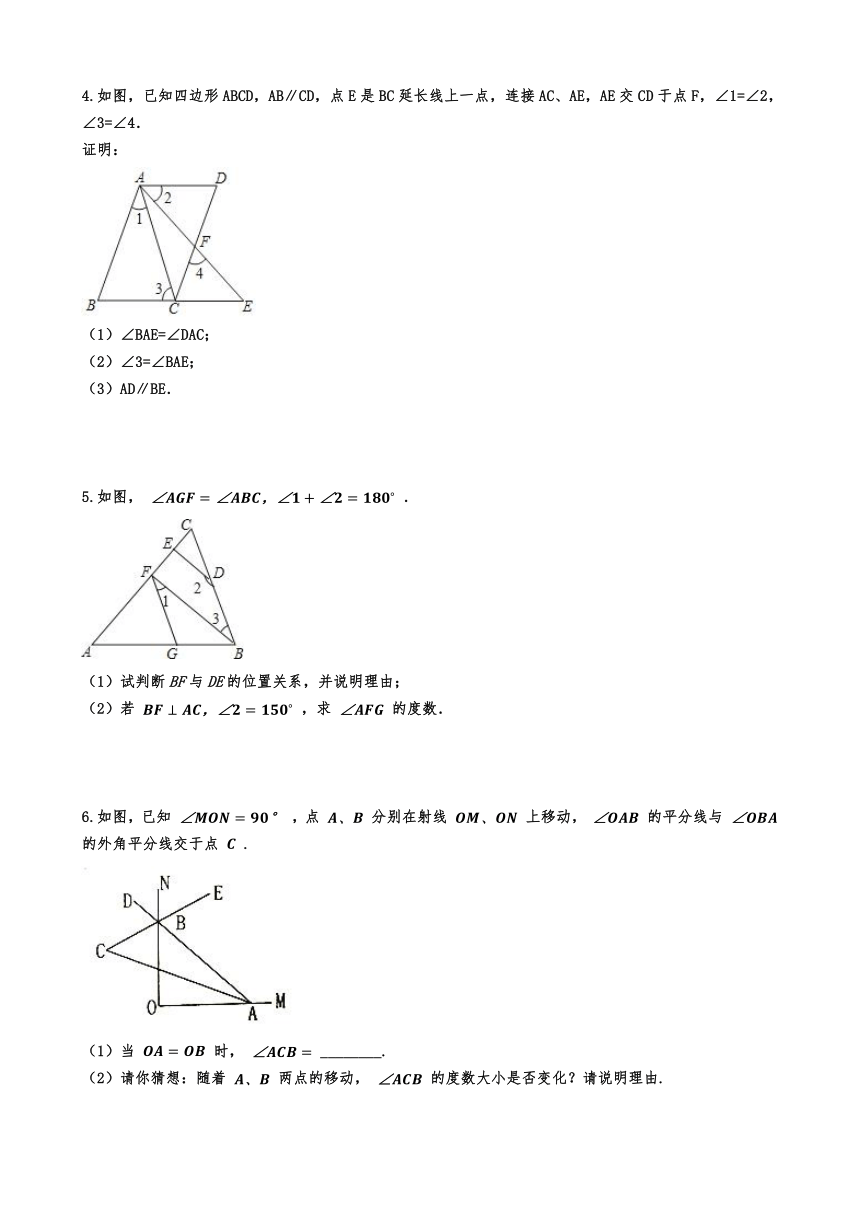
1.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=110°,求∠ACB的度数.
2.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.
(1)求证:AD∥BC;
(2)若∠1=36°,求∠2的度数.
3.已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
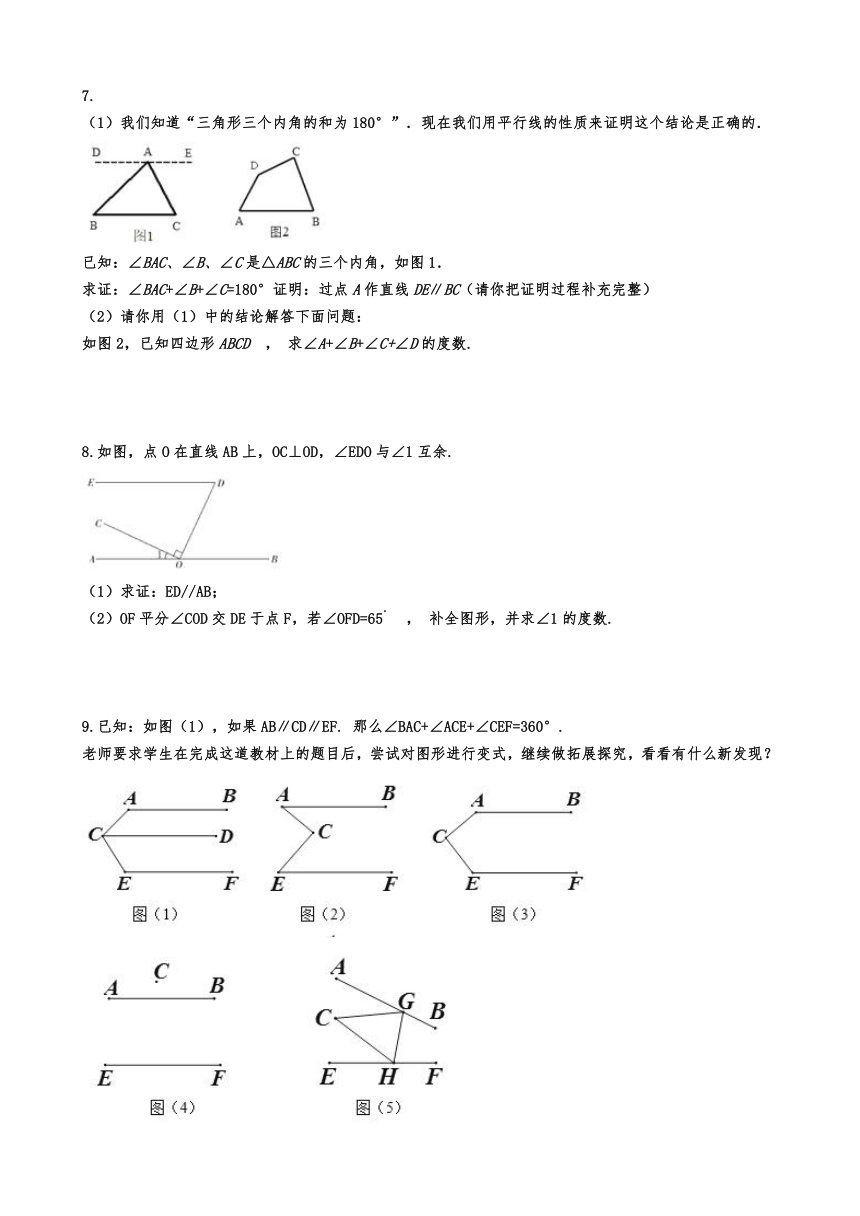
4.如图,已知四边形ABCD,AB∥CD,点E是BC延长线上一点,连接AC、AE,AE交CD于点F,∠1=∠2,∠3=∠4.
证明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
5.如图, .
(1)试判断BF与DE的位置关系,并说明理由;
(2)若 ,求 的度数.
6.如图,已知 ,点 分别在射线 上移动, 的平分线与 的外角平分线交于点 .
(1)当 时, ________.
(2)请你猜想:随着 两点的移动, 的度数大小是否变化?请说明理由.
7.???????????????
(1)我们知道“三角形三个内角的和为180°”.现在我们用平行线的性质来证明这个结论是正确的.
已知:∠BAC、∠B、∠C是△ABC的三个内角,如图1.
求证:∠BAC+∠B+∠C=180°证明:过点A作直线DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
如图2,已知四边形ABCD , 求∠A+∠B+∠C+∠D的度数.
8.如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65° , 补全图形,并求∠1的度数.
9.已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系:________.
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系:________.
(3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.
10.如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘AB、CD是否平行;
(2)若AB∥CD,连接BC,过点A作AM⊥BC于M,垂足为M,画出图形,并写出∠BCD与∠BAM的数量关系.
11.已知直线l1∥l2 , 直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
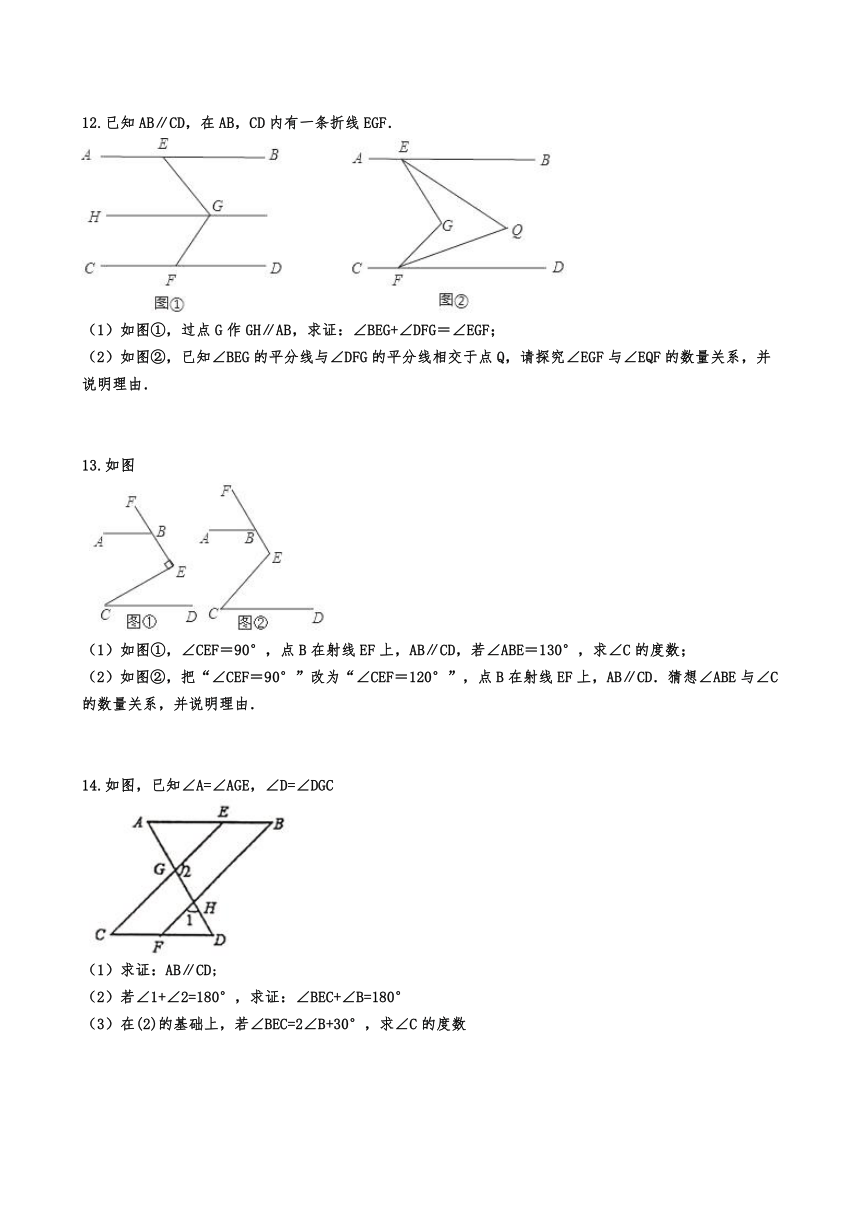
12.已知AB∥CD,在AB,CD内有一条折线EGF.
(1)如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;
(2)如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.
13.如图
(1)如图①,∠CEF=90°,点B在射线EF上,AB∥CD,若∠ABE=130°,求∠C的度数;
(2)如图②,把“∠CEF=90°”改为“∠CEF=120°”,点B在射线EF上,AB∥CD.猜想∠ABE与∠C的数量关系,并说明理由.
14.如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数
15.如图1,若AB∥CD,则∠B+∠D=∠BED
理由:如图,过点E作EF∥AB,
则∠B=∠BEF.(依据)
因为AB∥CD,
所以EF∥CD,
所以∠D=∠DEF
所以∠BED=∠BEF+∠DEF=∠B+∠D
(1)上述证明过程中的依据是指________。
(2)若将点E移至图2所示的位置,AB∥CD,此时∠B、∠D、∠E之间有什么关系?请说明理由。
(3)在图3中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?
16.已知直线 , 的顶点 与 分别在直线 与 上, ,设 , .
(1)如图①,当点 落在 的上方时, 与 相交于点 ,求证: ;
(2)如图②.当点 落在直线 的下方时, 与 交于点 ,请判断 与 的数量关系,并说明理由.
17.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
(1)图1中的∠ABC的度数为________.
(2)图2中已知AE∥BC,则∠AFD的度数为________.
18.问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(1)数学活动小组经过讨论形成下列推理,请你补全推理依据.
如图2,过点P作PE∥AB,
∵PE∥AB(作图知)
又∵AB∥CD,
∴PE∥CD.________
∴∠A+∠APE=180°.
∠C+∠CPE=180°.________
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=α,∠BCP=β,求∠CPD与α、β之间有何数量关系?请说明理由.
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与α、β之间的数量关系.
19.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点 P 在线段 AB 上,如图(1)所示,且∠α=50°,则∠1+∠2=________°;
(2)若点 P 在边 AB 上运动,如图(2)所示,则∠α、∠1、∠2 之间的关系为:________;
(3)若点P运动到边 AB 的延长线上,如图(3)所示,则∠α、∠1、∠2 之间有何关系?猜想并说明理由.
(4)若点P运动到△ABC 形外,如图(4)所示,则∠α、∠1、∠2 之间的关系为:________.
答案
1. (1)解:CD∥EF,
理由:∵ CD⊥AB,EF⊥AB?,
∴CD∥EF;
(2)解:∵CD∥EF,∴∠BCD=∠2,
∵∠1=∠2?,∴∠BCD=∠1,
∴DG∥BC,
∴∠ACB=∠3=110°.
2. (1)证明:∵∠ABC=180°-∠A ,
∴∠ABC+∠A=180°,
∴AD∥BC
(2)解:∵AD∥BC , ∠1=36°,
∴∠3=∠1=36°,
∵BD⊥CD , EF⊥CD ,
∴BD∥EF ,
∴∠2=∠3=36°
3. (1)证明:∵∠DAE=∠AEB,
∴BE∥AD,
∴∠D=∠EBD,
∵∠D=∠BEC,
∴∠BEC=∠EBD,
∴BD∥EC
(2)解:∵BD∥CE,BE∥AD,
∴∠C=∠DBA,∠EBC=∠DAC,
∵∠C=70°,∠DAC=50°,
∴∠DBA=70°,∠EBC=50°,
∴DBE=180°-∠DBA-∠EBC=60°.
4.(1)证明:∵∠1=∠2,
∴∠1+∠CAE=∠2+∠CAE,
即∠BAE=∠DAC
(2)证明:∵AB∥CD,
∴∠4=∠BAE,
∵∠3=∠4,
∴∠3=∠BAE
(3)证明:∵∠3=∠BAE,∠BAE=∠DAC,
∴∠3=∠DAC,
∴AD∥BE.
5. (1)解:BF∥DE,理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE
(2)解:∵BF⊥AC,
∴∠AFB=90°,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∴∠AFG=∠AFB-∠1=90°-30°=60°.
6. (1)45°
(2)解:随着 两点的移动, 的度数大小不会变化.
理由如下:
∵ 平分
∴
∵ 平分
∴
∵ 是 的一个外角
∴
∴
∵ 是 的一个外角
∴
∴
7. (1)证明:过点A作PQ∥BC
∴∠1=∠B(两直线平行,内错角相等)
∠2=∠C(两直线平行,内错角相等)
又∵∠1+∠2+∠3=180°(平角的定义)
∴∠BAC+∠B+∠C=180°(等量代换)
(2)连接AC.得到两个三角形△ABC和△ADC
∵三角形内角和是180°,所以两个就是360°.
∴∠A+∠B+∠C+∠D=360°
8. (1)证明:∵∠EDO与∠1互余,
∴∠EDO+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠EDO+∠1+∠COD=180°,
∴∠EDO+∠AOD=180°,
∴ED∥AB
(2)解:如图所示:
∵ED∥AB,
∴∠AOF=∠OFD=65°,
∵OF平分∠COD,
∴∠COF= ∠COD=45°,
∴∠1=∠AOF-∠COF=20°
9. (1)两直线平行,同旁内角互补
(2)∠ACE=∠BAC+∠FEC;∠ACE=∠FEC-∠BAC
(3)解:延长AB,EF,交于点P,如图,
∵GH同时平分∠BGC和∠FHC,
∴∠CGH=∠BGH,∠CHG=∠FHG,
∴∠C=∠P,
∵∠CGP=180°-∠AGC,∠CHP=180°-∠CHE,
∴∠CGP+∠CHP=360°-(∠AGC+∠CHE),
∵四边形GCHP中,∠C+∠P=360°-(∠CGP+∠CH)=360°-[360°-(∠AGC+∠CHE)]= ∠AGC+∠CHE,
即2∠GCH=∠AGC+∠CHE
10. (1)解:根据同位角相等,两直线平行,可以画一条直线截线段 AB 与CD,测量一对同位角,如果相等,则 AB∥CD,反之,则不平行.
(2)解:如图所示:
∵AB∥CD,
∴∠BCD=∠ABC,
∵AM⊥BC,
∴∠ABC+∠BAM=90°, 则∠BCD+∠BAM=90°.
11. (1)解:∠APB=∠PAC+∠PBD,
如图1,过点P作PE∥l1 ,
∴∠APE=∠PAC,
∵l1∥l2
∴PE∥l2 ,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠BAC+∠PBD,
∴∠APB=∠PAC+∠PBD;
(2)解:不成立,
如图2:∠PAC=∠APB+∠PBD,
理由:过点P作PE∥l1 ,
∴∠APE=∠PAC,
∵l1∥l2 ,
∴PE∥l2 ,
∴∠BPE=∠PBD
∵∠APB=∠APE-∠BPE=∠PAC-∠PBD
∴∠PAC=∠APB+∠PBD;
如图3:∠PBD=∠PAC+∠APB,
理由:过点P作PE∥l1 ,
∴∠APE=∠PAC,
∵l1∥l2 ,
∴PE∥l2 ,
∴∠BPE=∠PBD,
∵∠APB=∠BPE-∠APE=∠PBD-∠PAC,
∴∠PBD=∠PAC+∠APB
12. (1)解:∵GH∥AB,AB∥CD,
∴GH∥CD,
∴∠EGH=∠BEG,∠DFG=∠FGH,
∵∠EGF=∠EGH+∠FGH,
∴∠BEG+∠DFG=∠EGF
(2)解:由(1)知,∠EGF=∠BEG+∠DFG,∠EQF=∠BEQ+∠DFQ,
∵EQ,FQ分别平分∠BEG,∠DFG,
∴∠DFQ= DFG,∠BEQ= BEG,
∴∠EQF= (∠BEG+∠DFG)= EGF
13.(1)解:如图①,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°﹣∠ABE=50°,
∵∠CEF=90°,
∴∠2=90°﹣∠1=40°,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2=40°
(2)解:∠ABE﹣∠C=60°,
理由:如图②,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°﹣∠ABE,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2,
∵∠CEF=∠1+∠2=120°,即180°﹣∠ABE+∠C=120°,
∴∠ABE﹣∠C=180°﹣120°=60°.
14.(1)证明:∵ ,
又∵
?∴
∴
(2)证明:∵ ,
∴
∴
∴
(3)解:∵ ,
∴
∴
又∵ ,
∴ ,
∴
15. (1)解:两直线平行,内错角相等
(2)解:∠BED+∠B+∠D=360°
理由:如图1,过E点作EF∥AB,
所以∠BEF+∠B=180°
因为AB∥CD,所以EF∥CD
所以∠D+∠DEF=180°,
∠BED+∠B+∠D=360°
(3)解:如图2,
分别过折点E、F、G作AB的平行线EE1、FF1、GG1
因为AB∥CD
所以AB∥EE1∥FF1∥GG1∥CD
所以∠B=∠BEE1 , ∠E1EF=∠EFF1 , ∠F1FG=∠FGG1 , ∠G1GD=∠D
所以∠BEF+∠FGD=∠B+∠EFG+∠D…
16.(1)解: 是 的一个外角,
,
,
,
,
,
(2)解: ,理由如下:
是 的一个外角,
,
,
,
,
,
17. (1)75°
(2)75°
18. (1)平行于同一条直线的两条直线平行;两直线平行同旁内角互补
问题迁移:
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
问题解决:
(3)∠CPD=∠β-∠α或∠CPD=∠α-∠β.
19. (1)140
(2)∠1+∠2=90°+α
(3)解:∠1=90°+∠2+α,
理由:∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+α=90°+∠2+α.
(4)∠2=90°+∠1﹣α
1.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=110°,求∠ACB的度数.
2.如图,已知∠ABC=180°﹣∠A,BD⊥CD于D,EF⊥CD于F.
(1)求证:AD∥BC;
(2)若∠1=36°,求∠2的度数.
3.已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
4.如图,已知四边形ABCD,AB∥CD,点E是BC延长线上一点,连接AC、AE,AE交CD于点F,∠1=∠2,∠3=∠4.
证明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
5.如图, .
(1)试判断BF与DE的位置关系,并说明理由;
(2)若 ,求 的度数.
6.如图,已知 ,点 分别在射线 上移动, 的平分线与 的外角平分线交于点 .
(1)当 时, ________.
(2)请你猜想:随着 两点的移动, 的度数大小是否变化?请说明理由.
7.???????????????
(1)我们知道“三角形三个内角的和为180°”.现在我们用平行线的性质来证明这个结论是正确的.
已知:∠BAC、∠B、∠C是△ABC的三个内角,如图1.
求证:∠BAC+∠B+∠C=180°证明:过点A作直线DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
如图2,已知四边形ABCD , 求∠A+∠B+∠C+∠D的度数.
8.如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65° , 补全图形,并求∠1的度数.
9.已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系:________.
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系:________.
(3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.
10.如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘AB、CD是否平行;
(2)若AB∥CD,连接BC,过点A作AM⊥BC于M,垂足为M,画出图形,并写出∠BCD与∠BAM的数量关系.
11.已知直线l1∥l2 , 直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
12.已知AB∥CD,在AB,CD内有一条折线EGF.
(1)如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;
(2)如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.
13.如图
(1)如图①,∠CEF=90°,点B在射线EF上,AB∥CD,若∠ABE=130°,求∠C的度数;
(2)如图②,把“∠CEF=90°”改为“∠CEF=120°”,点B在射线EF上,AB∥CD.猜想∠ABE与∠C的数量关系,并说明理由.
14.如图,已知∠A=∠AGE,∠D=∠DGC
(1)求证:AB∥CD;
(2)若∠1+∠2=180°,求证:∠BEC+∠B=180°
(3)在(2)的基础上,若∠BEC=2∠B+30°,求∠C的度数
15.如图1,若AB∥CD,则∠B+∠D=∠BED
理由:如图,过点E作EF∥AB,
则∠B=∠BEF.(依据)
因为AB∥CD,
所以EF∥CD,
所以∠D=∠DEF
所以∠BED=∠BEF+∠DEF=∠B+∠D
(1)上述证明过程中的依据是指________。
(2)若将点E移至图2所示的位置,AB∥CD,此时∠B、∠D、∠E之间有什么关系?请说明理由。
(3)在图3中,AB∥CD,∠E+∠G与∠B+∠F+∠D又有何关系?
16.已知直线 , 的顶点 与 分别在直线 与 上, ,设 , .
(1)如图①,当点 落在 的上方时, 与 相交于点 ,求证: ;
(2)如图②.当点 落在直线 的下方时, 与 交于点 ,请判断 与 的数量关系,并说明理由.
17.生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如图两幅图都是由同一副三角板拼凑得到的:
(1)图1中的∠ABC的度数为________.
(2)图2中已知AE∥BC,则∠AFD的度数为________.
18.问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(1)数学活动小组经过讨论形成下列推理,请你补全推理依据.
如图2,过点P作PE∥AB,
∵PE∥AB(作图知)
又∵AB∥CD,
∴PE∥CD.________
∴∠A+∠APE=180°.
∠C+∠CPE=180°.________
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=α,∠BCP=β,求∠CPD与α、β之间有何数量关系?请说明理由.
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与α、β之间的数量关系.
19.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点 P 在线段 AB 上,如图(1)所示,且∠α=50°,则∠1+∠2=________°;
(2)若点 P 在边 AB 上运动,如图(2)所示,则∠α、∠1、∠2 之间的关系为:________;
(3)若点P运动到边 AB 的延长线上,如图(3)所示,则∠α、∠1、∠2 之间有何关系?猜想并说明理由.
(4)若点P运动到△ABC 形外,如图(4)所示,则∠α、∠1、∠2 之间的关系为:________.
答案
1. (1)解:CD∥EF,
理由:∵ CD⊥AB,EF⊥AB?,
∴CD∥EF;
(2)解:∵CD∥EF,∴∠BCD=∠2,
∵∠1=∠2?,∴∠BCD=∠1,
∴DG∥BC,
∴∠ACB=∠3=110°.
2. (1)证明:∵∠ABC=180°-∠A ,
∴∠ABC+∠A=180°,
∴AD∥BC
(2)解:∵AD∥BC , ∠1=36°,
∴∠3=∠1=36°,
∵BD⊥CD , EF⊥CD ,
∴BD∥EF ,
∴∠2=∠3=36°
3. (1)证明:∵∠DAE=∠AEB,
∴BE∥AD,
∴∠D=∠EBD,
∵∠D=∠BEC,
∴∠BEC=∠EBD,
∴BD∥EC
(2)解:∵BD∥CE,BE∥AD,
∴∠C=∠DBA,∠EBC=∠DAC,
∵∠C=70°,∠DAC=50°,
∴∠DBA=70°,∠EBC=50°,
∴DBE=180°-∠DBA-∠EBC=60°.
4.(1)证明:∵∠1=∠2,
∴∠1+∠CAE=∠2+∠CAE,
即∠BAE=∠DAC
(2)证明:∵AB∥CD,
∴∠4=∠BAE,
∵∠3=∠4,
∴∠3=∠BAE
(3)证明:∵∠3=∠BAE,∠BAE=∠DAC,
∴∠3=∠DAC,
∴AD∥BE.
5. (1)解:BF∥DE,理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE
(2)解:∵BF⊥AC,
∴∠AFB=90°,
∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∴∠AFG=∠AFB-∠1=90°-30°=60°.
6. (1)45°
(2)解:随着 两点的移动, 的度数大小不会变化.
理由如下:
∵ 平分
∴
∵ 平分
∴
∵ 是 的一个外角
∴
∴
∵ 是 的一个外角
∴
∴
7. (1)证明:过点A作PQ∥BC
∴∠1=∠B(两直线平行,内错角相等)
∠2=∠C(两直线平行,内错角相等)
又∵∠1+∠2+∠3=180°(平角的定义)
∴∠BAC+∠B+∠C=180°(等量代换)
(2)连接AC.得到两个三角形△ABC和△ADC
∵三角形内角和是180°,所以两个就是360°.
∴∠A+∠B+∠C+∠D=360°
8. (1)证明:∵∠EDO与∠1互余,
∴∠EDO+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠EDO+∠1+∠COD=180°,
∴∠EDO+∠AOD=180°,
∴ED∥AB
(2)解:如图所示:
∵ED∥AB,
∴∠AOF=∠OFD=65°,
∵OF平分∠COD,
∴∠COF= ∠COD=45°,
∴∠1=∠AOF-∠COF=20°
9. (1)两直线平行,同旁内角互补
(2)∠ACE=∠BAC+∠FEC;∠ACE=∠FEC-∠BAC
(3)解:延长AB,EF,交于点P,如图,
∵GH同时平分∠BGC和∠FHC,
∴∠CGH=∠BGH,∠CHG=∠FHG,
∴∠C=∠P,
∵∠CGP=180°-∠AGC,∠CHP=180°-∠CHE,
∴∠CGP+∠CHP=360°-(∠AGC+∠CHE),
∵四边形GCHP中,∠C+∠P=360°-(∠CGP+∠CH)=360°-[360°-(∠AGC+∠CHE)]= ∠AGC+∠CHE,
即2∠GCH=∠AGC+∠CHE
10. (1)解:根据同位角相等,两直线平行,可以画一条直线截线段 AB 与CD,测量一对同位角,如果相等,则 AB∥CD,反之,则不平行.
(2)解:如图所示:
∵AB∥CD,
∴∠BCD=∠ABC,
∵AM⊥BC,
∴∠ABC+∠BAM=90°, 则∠BCD+∠BAM=90°.
11. (1)解:∠APB=∠PAC+∠PBD,
如图1,过点P作PE∥l1 ,
∴∠APE=∠PAC,
∵l1∥l2
∴PE∥l2 ,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠BAC+∠PBD,
∴∠APB=∠PAC+∠PBD;
(2)解:不成立,
如图2:∠PAC=∠APB+∠PBD,
理由:过点P作PE∥l1 ,
∴∠APE=∠PAC,
∵l1∥l2 ,
∴PE∥l2 ,
∴∠BPE=∠PBD
∵∠APB=∠APE-∠BPE=∠PAC-∠PBD
∴∠PAC=∠APB+∠PBD;
如图3:∠PBD=∠PAC+∠APB,
理由:过点P作PE∥l1 ,
∴∠APE=∠PAC,
∵l1∥l2 ,
∴PE∥l2 ,
∴∠BPE=∠PBD,
∵∠APB=∠BPE-∠APE=∠PBD-∠PAC,
∴∠PBD=∠PAC+∠APB
12. (1)解:∵GH∥AB,AB∥CD,
∴GH∥CD,
∴∠EGH=∠BEG,∠DFG=∠FGH,
∵∠EGF=∠EGH+∠FGH,
∴∠BEG+∠DFG=∠EGF
(2)解:由(1)知,∠EGF=∠BEG+∠DFG,∠EQF=∠BEQ+∠DFQ,
∵EQ,FQ分别平分∠BEG,∠DFG,
∴∠DFQ= DFG,∠BEQ= BEG,
∴∠EQF= (∠BEG+∠DFG)= EGF
13.(1)解:如图①,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°﹣∠ABE=50°,
∵∠CEF=90°,
∴∠2=90°﹣∠1=40°,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2=40°
(2)解:∠ABE﹣∠C=60°,
理由:如图②,过E作EK∥AB,则∠ABE+∠1=180°,
∴∠1=180°﹣∠ABE,
∵AB∥CD,EK∥AB,
∴EK∥CD,
∴∠C=∠2,
∵∠CEF=∠1+∠2=120°,即180°﹣∠ABE+∠C=120°,
∴∠ABE﹣∠C=180°﹣120°=60°.
14.(1)证明:∵ ,
又∵
?∴
∴
(2)证明:∵ ,
∴
∴
∴
(3)解:∵ ,
∴
∴
又∵ ,
∴ ,
∴
15. (1)解:两直线平行,内错角相等
(2)解:∠BED+∠B+∠D=360°
理由:如图1,过E点作EF∥AB,
所以∠BEF+∠B=180°
因为AB∥CD,所以EF∥CD
所以∠D+∠DEF=180°,
∠BED+∠B+∠D=360°
(3)解:如图2,
分别过折点E、F、G作AB的平行线EE1、FF1、GG1
因为AB∥CD
所以AB∥EE1∥FF1∥GG1∥CD
所以∠B=∠BEE1 , ∠E1EF=∠EFF1 , ∠F1FG=∠FGG1 , ∠G1GD=∠D
所以∠BEF+∠FGD=∠B+∠EFG+∠D…
16.(1)解: 是 的一个外角,
,
,
,
,
,
(2)解: ,理由如下:
是 的一个外角,
,
,
,
,
,
17. (1)75°
(2)75°
18. (1)平行于同一条直线的两条直线平行;两直线平行同旁内角互补
问题迁移:
(2)∠CPD=∠α+∠β,
理由是:如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
问题解决:
(3)∠CPD=∠β-∠α或∠CPD=∠α-∠β.
19. (1)140
(2)∠1+∠2=90°+α
(3)解:∠1=90°+∠2+α,
理由:∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+α=90°+∠2+α.
(4)∠2=90°+∠1﹣α
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
