冀教版数学七年级下册7.2 相交线 第1课时 课件(27张ppt)
文档属性
| 名称 | 冀教版数学七年级下册7.2 相交线 第1课时 课件(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 00:40:46 | ||
图片预览




文档简介
课件27张PPT。第七章
相交线与平行线7.2 相交线
第1课时冀教版数学七年级下册1.理解掌握对顶角的概念及其性质.(重点)
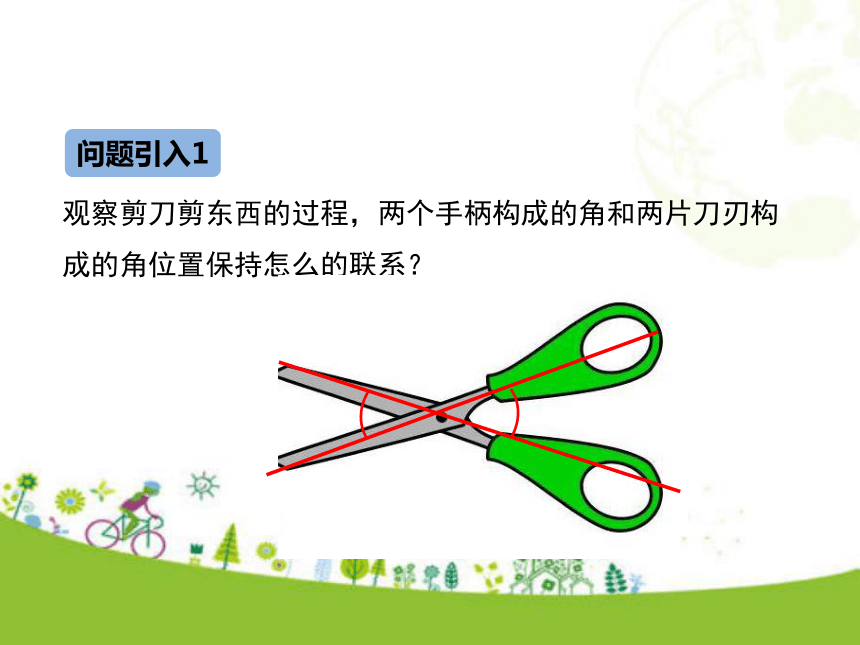
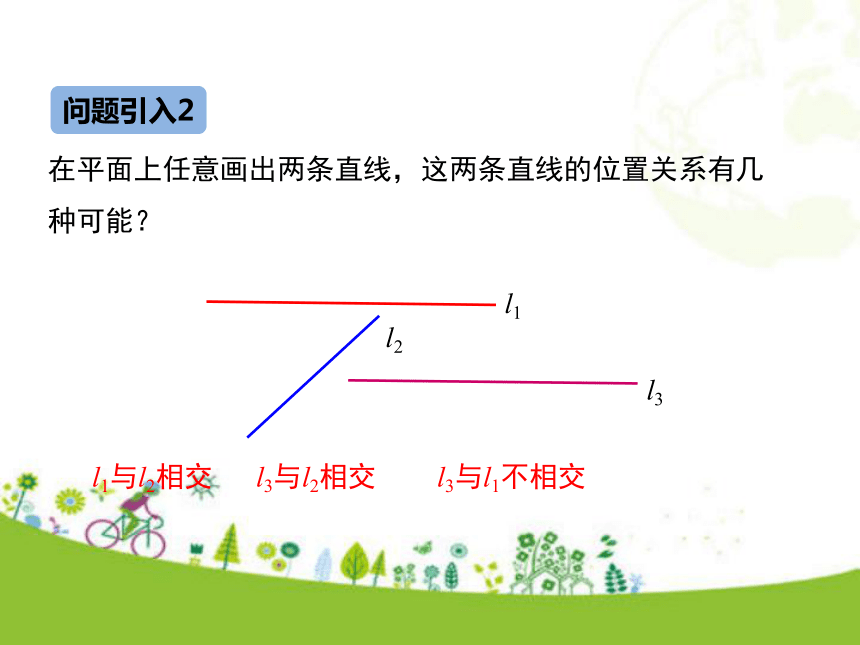
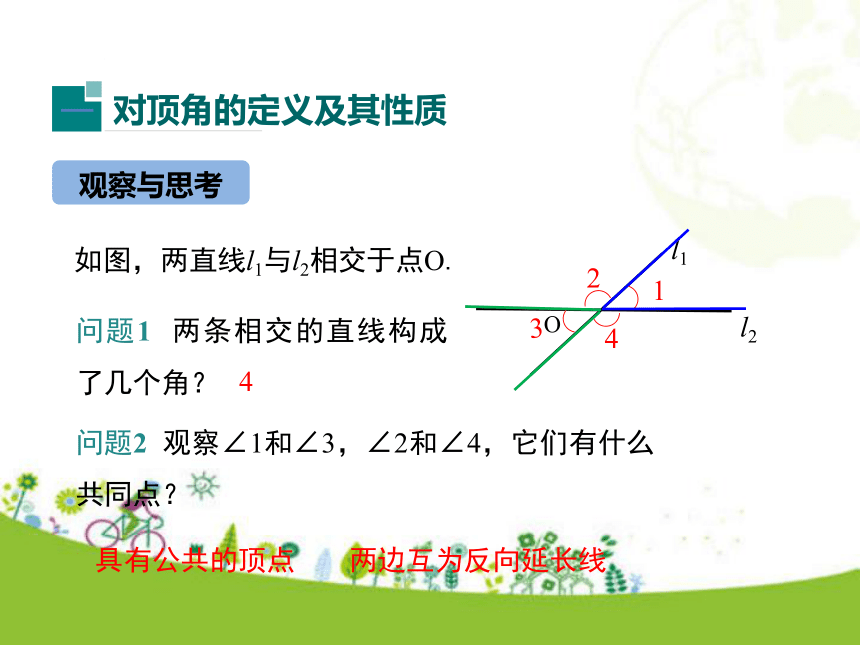
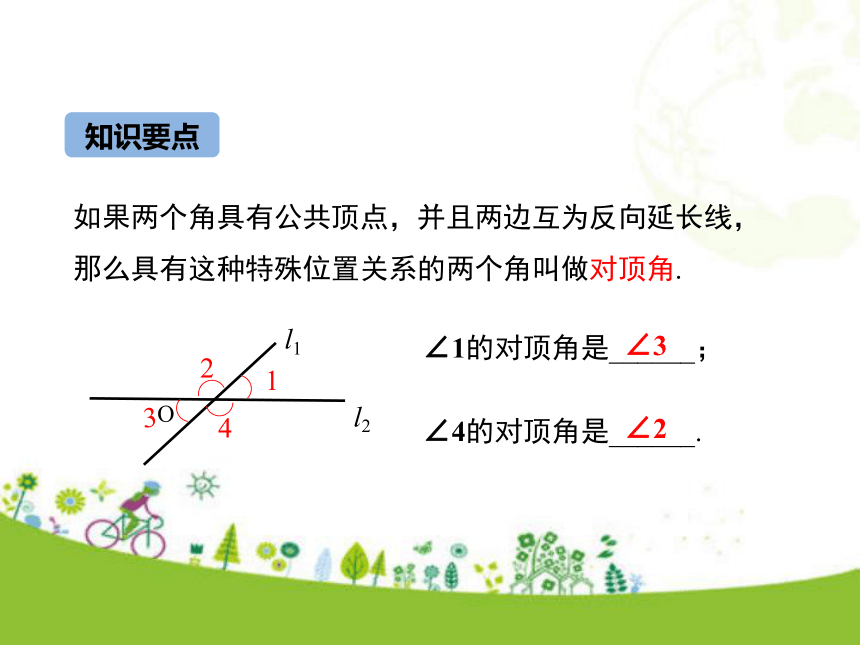
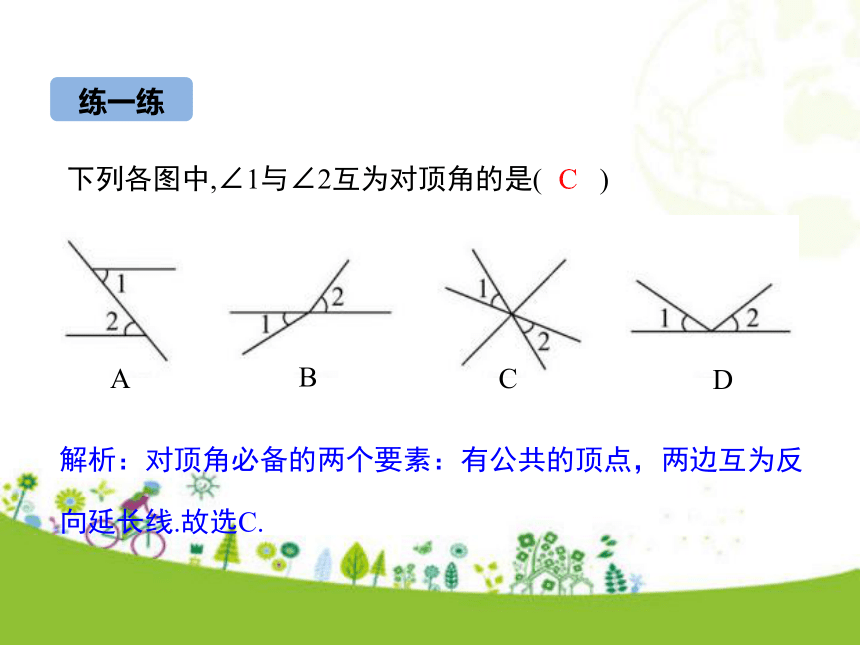
2.理解掌握同位角、内错角、同旁内角的概念.(重点)学习目标情境引入问题引入1观察剪刀剪东西的过程,两个手柄构成的角和两片刀刃构成的角位置保持怎么的联系?问题引入2在平面上任意画出两条直线,这两条直线的位置关系有几种可能?l1与l2相交l1l2l3l3与l2相交l3与l1不相交观察与思考问题1 两条相交的直线构成了几个角? 4问题2 观察∠1和∠3,∠2和∠4,它们有什么共同点? 具有公共的顶点两边互为反向延长线知识要点如果两个角具有公共顶点,并且两边互为反向延长线,那么具有这种特殊位置关系的两个角叫做对顶角.∠1的对顶角是______;∠4的对顶角是______.∠3∠2下列各图中,∠1与∠2互为对顶角的是( ) 练一练ABCD解析:对顶角必备的两个要素:有公共的顶点,两边互为反向延长线.故选C.C问题3 当直线l1绕点O旋转时,∠1和∠3的有什么变化?你能猜想出∠1和∠3的大小关系吗?l2l1O∠1和∠3同时增大∠1和∠3同时减小OABCD问题4 你能用测量、折叠或是旋转的方法验证你的猜想吗?问题5 你能用说理的方法来验证你的猜想吗?理由:因为∠1和∠2互补,∠2和∠3互补,所以∠1=∠3(同角的补角相等).练一练如图,直线a、b相交,∠1=40°,求 ∠2,∠3,∠4的度数.∵∠3=∠1,∠1=40° , ∴∠3=40°.解:∴∠2=180°-∠1=140°.∴∠4=∠2=140°.观察与思考问题1 如图,一条直线c,分别于两条直线a,b相交(也说直线a,b被直线所截,构成了几个角?问题2 观察∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8的位置关系,试描述它们的位置特征.F①在直线c的同旁(右边)②在直线a,b的同一侧(上方)abc12345678同位角问题2 观察∠3和∠6,∠4和∠5,试描述它们的位置特征.abcF12345678①在直线c的同旁②在直线a,b的之间同旁内角abc12345678①在直线c的两侧②在直线a,b的之间内错角问题3 观察∠3和∠5,∠4和∠6,试描述它们的位置特征. 例1 如图,直线DE截直线AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角. 解:两条直线是AB,AC,截线是DE,所以8个角中,
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.典例精析图形特征:在形如字母“F”的图形中有同位角. 变式图形:图中的∠1与∠2都是同位角.要点归纳变式图形:图中的∠1与∠2都是同旁内角.图形特征:在形如“U”的图形中有同旁内角. 变式图形:图中的∠1与∠2都是内错角图形特征:在形如“Z”的图形中有内错角。如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角.
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.练一练当堂练习1.如图,∠DAB和∠ABC是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对2.如图,∠1和∠2不能构成同位角的图形是 ( ) CB3.如图:找出图中数字标注的角的对顶角,同位角,内错角,同旁内角.解:对顶角:∠1和∠4;同位角:∠5和∠4;内错角:∠5和∠1,∠6和∠3;同旁内角角:∠5和∠6. 4.如图,直线AB,CD,EF相交于点O.
(1)写出∠DOA, ∠EOC的对顶角;
(2)如果∠AOC =50°,求∠BOD ,∠COB的度数.AEDBFCO解:(1)∠DOA的对顶角为∠COB,
∠EOC的对顶角为∠DOF.(2) 因为∠AOC=50°,
所以∠BOD=∠AOC=50°,
所以∠COB=∠180°-∠AOC=130°.5.如图,直线AB,CD相交于点O, ∠EOC=70°,OA平分∠EOC,求∠BOD的度数.BDACEO解:因为∠EOC=70°,OA平分
∠EOC,所以∠BOD=∠AOC=35°.课堂小结对顶角和三线八角三线八角定义性质具有公共定点,两边互为反向延长线对顶角相等同位角同旁内角内错角F形U形Z形对顶角谢谢!
相交线与平行线7.2 相交线
第1课时冀教版数学七年级下册1.理解掌握对顶角的概念及其性质.(重点)
2.理解掌握同位角、内错角、同旁内角的概念.(重点)学习目标情境引入问题引入1观察剪刀剪东西的过程,两个手柄构成的角和两片刀刃构成的角位置保持怎么的联系?问题引入2在平面上任意画出两条直线,这两条直线的位置关系有几种可能?l1与l2相交l1l2l3l3与l2相交l3与l1不相交观察与思考问题1 两条相交的直线构成了几个角? 4问题2 观察∠1和∠3,∠2和∠4,它们有什么共同点? 具有公共的顶点两边互为反向延长线知识要点如果两个角具有公共顶点,并且两边互为反向延长线,那么具有这种特殊位置关系的两个角叫做对顶角.∠1的对顶角是______;∠4的对顶角是______.∠3∠2下列各图中,∠1与∠2互为对顶角的是( ) 练一练ABCD解析:对顶角必备的两个要素:有公共的顶点,两边互为反向延长线.故选C.C问题3 当直线l1绕点O旋转时,∠1和∠3的有什么变化?你能猜想出∠1和∠3的大小关系吗?l2l1O∠1和∠3同时增大∠1和∠3同时减小OABCD问题4 你能用测量、折叠或是旋转的方法验证你的猜想吗?问题5 你能用说理的方法来验证你的猜想吗?理由:因为∠1和∠2互补,∠2和∠3互补,所以∠1=∠3(同角的补角相等).练一练如图,直线a、b相交,∠1=40°,求 ∠2,∠3,∠4的度数.∵∠3=∠1,∠1=40° , ∴∠3=40°.解:∴∠2=180°-∠1=140°.∴∠4=∠2=140°.观察与思考问题1 如图,一条直线c,分别于两条直线a,b相交(也说直线a,b被直线所截,构成了几个角?问题2 观察∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8的位置关系,试描述它们的位置特征.F①在直线c的同旁(右边)②在直线a,b的同一侧(上方)abc12345678同位角问题2 观察∠3和∠6,∠4和∠5,试描述它们的位置特征.abcF12345678①在直线c的同旁②在直线a,b的之间同旁内角abc12345678①在直线c的两侧②在直线a,b的之间内错角问题3 观察∠3和∠5,∠4和∠6,试描述它们的位置特征. 例1 如图,直线DE截直线AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角. 解:两条直线是AB,AC,截线是DE,所以8个角中,
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.典例精析图形特征:在形如字母“F”的图形中有同位角. 变式图形:图中的∠1与∠2都是同位角.要点归纳变式图形:图中的∠1与∠2都是同旁内角.图形特征:在形如“U”的图形中有同旁内角. 变式图形:图中的∠1与∠2都是内错角图形特征:在形如“Z”的图形中有内错角。如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
(2)如果∠1=∠4,那么∠1与∠2相等吗?∠1与∠3互补吗?为什么?解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角.
(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,所以∠4+∠3=180°,即∠1与∠3互补.练一练当堂练习1.如图,∠DAB和∠ABC是 ( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对2.如图,∠1和∠2不能构成同位角的图形是 ( ) CB3.如图:找出图中数字标注的角的对顶角,同位角,内错角,同旁内角.解:对顶角:∠1和∠4;同位角:∠5和∠4;内错角:∠5和∠1,∠6和∠3;同旁内角角:∠5和∠6. 4.如图,直线AB,CD,EF相交于点O.
(1)写出∠DOA, ∠EOC的对顶角;
(2)如果∠AOC =50°,求∠BOD ,∠COB的度数.AEDBFCO解:(1)∠DOA的对顶角为∠COB,
∠EOC的对顶角为∠DOF.(2) 因为∠AOC=50°,
所以∠BOD=∠AOC=50°,
所以∠COB=∠180°-∠AOC=130°.5.如图,直线AB,CD相交于点O, ∠EOC=70°,OA平分∠EOC,求∠BOD的度数.BDACEO解:因为∠EOC=70°,OA平分
∠EOC,所以∠BOD=∠AOC=35°.课堂小结对顶角和三线八角三线八角定义性质具有公共定点,两边互为反向延长线对顶角相等同位角同旁内角内错角F形U形Z形对顶角谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
