冀教版数学七年级下册7.3 平行线 课件(21张ppt)
文档属性
| 名称 | 冀教版数学七年级下册7.3 平行线 课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 07:55:57 | ||
图片预览






文档简介
课件21张PPT。第七章
相交线与平行线7.3 平行线冀教版数学七年级下册1.理解平行的概念,掌握两条平行线间的距离处处相等.(重点)
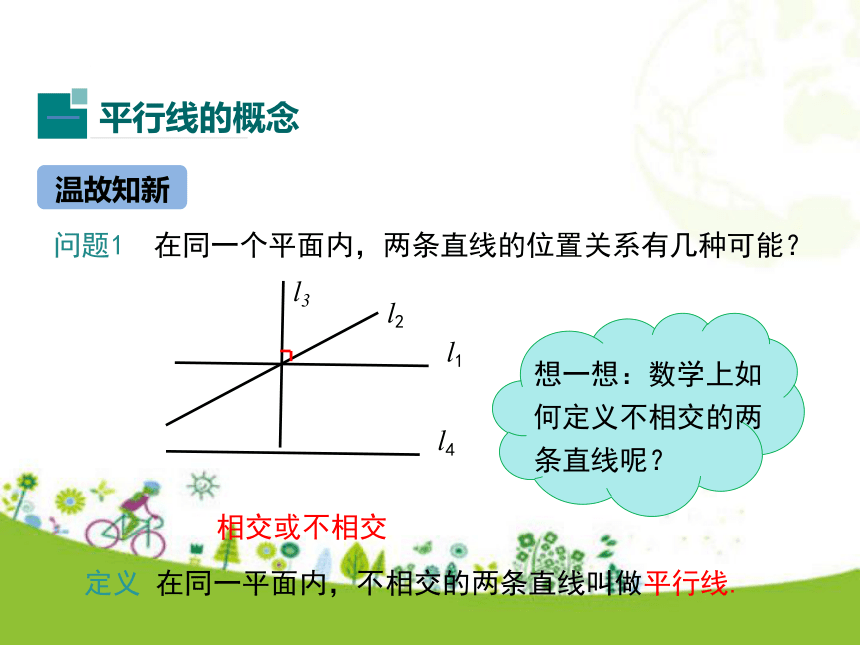
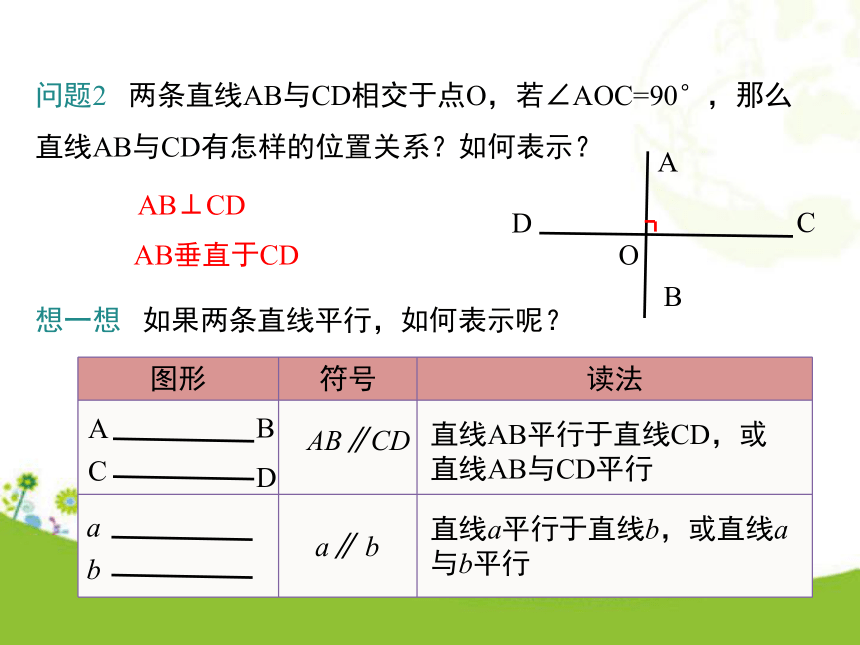
2.掌握有关平行线的两个基本事实.(难点)学习目标情境引入问题1 在同一个平面内,两条直线的位置关系有几种可能? 温故知新相交或不相交定义 在同一平面内,不相交的两条直线叫做平行线.问题2 两条直线AB与CD相交于点O,若∠AOC=90°,那么直线AB与CD有怎样的位置关系?如何表示?AB⊥CD想一想 如果两条直线平行,如何表示呢?AB垂直于CDAB∥CDa∥ b直线AB平行于直线CD,或直线AB与CD平行直线a平行于直线b,或直线a与b平行下列说法中正确的是( )
A.如果同一平面内的两条线段不相交,那么这两条线所在直线互相平行
B.不相交的两条直线一定是平行线
C.同一平面内两条射线不相交,则这两条射线互相平行
D.同一平面内有两条直线不相交,这两条直线一定是平行线 练一练D平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
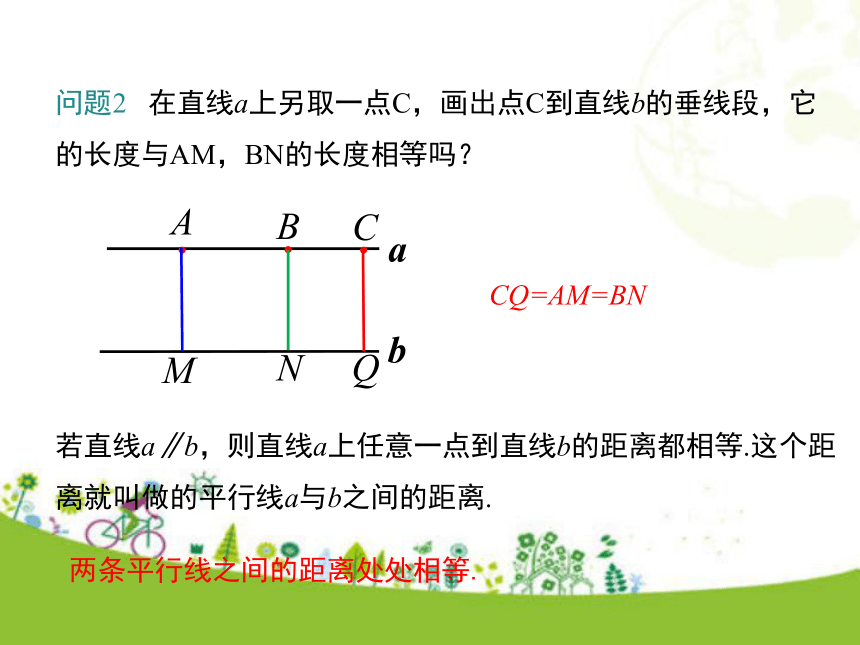
(3)平行线指的是“两条直线”而不是两条射线或两条线段.方法归纳AM=BN 合作探究如图,直线a∥b. A,B为直线a上任意两点.问题1 请用三角尺分别画出点A和点B到直线b的垂线段AM,BN,观察并度量AM和BN,看看它们的长度有什么关系? M N 问题2 在直线a上另取一点C,画出点C到直线b的垂线段,它的长度与AM,BN的长度相等吗? M N Q CQ=AM=BN若直线a∥b,则直线a上任意一点到直线b的距离都相等.这个距离就叫做的平行线a与b之间的距离.两条平行线之间的距离处处相等.1.平行线之间的距离是指( )
A.从一条直线上一点到另一直线的垂线段
B.从一条直线上一点到另一条直线的垂线段长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度 练一练B2.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
A.2cm B.6cm C.8cm D.2cm或8cm 解析:如图1,直线a和b之间的距离为:5-3=2(cm);
如图2,直线a和b之间的距离为:5+3=8(cm).故选DD观察与思考问题1 已知直线a,如何画出另一条直线b,使它与直线a平行? b问题2 如果直线a外任意取一点C,例能过点C画出与直线a平行的直线吗?这样的直线能画出多少条? a1条基本事实 经过直线外一点,有且只有一条直线和已知直线平行.问题3 如图,只要哪对角相等,就可使a∥b? 基本事实 同位角相等,两直线平行.典例精析例 如图,∠1=55°,∠2=55°.直线a与b平行吗?为什么? 解:a∥b.理由是:因为 ∠1=55°,∠2=55°,(已知)所以 ∠1=∠2(等量代换).所以 a∥b (同位角相等,两直线平行).在对命题进行说理的过程中,经常会使用“因为”“所以”两个词,未简单起见,今后我们用符号“∵”表示“因为”,用“∴”表示“所以”.当堂练习2.已知直线a∥b∥c,a与b的距离为5cm,b与c的距离为2cm,则a与c的距离是( )
A.3cm B.7cm C.3cm或7cm D.以上都不对
1.如图,a∥b,下列线段中是a,b之间的距离的是( )
A.AB B.AE C.EF D.BC CC3.填空
如图,点C,D,E在同一条直线上,∠1=130°,∠3=50°,CF与AD平行吗?请将下面的说理过程补充完整;123∵∠1=130°(已知),∴∠2=__________________
(互为补角的定义).180°-∠1=50°∵∠3=50°(已知),∴∠___=∠_____(等量代换).∴_____∥_____( ).F23CFAD同位角相等,两直线平行CDABE4.填空
(1)如图1,∠C=60°,当∠ABE=————°时,就能使BE∥CD;
(2)如图2 , ∠1=120°,∠2=60°,则a____b. 图1图2∥ ABECD12ab 603c课堂小结平行线定义平行线间的距离两个基本事实在_____________,不______的两条______叫做平行线直线AB平行于直线CD,记作“__________”直线 a∥b,则直线a上任意一点到直线b的______叫做平行线a,b之间的距离两条平行线之间的距离__________经过已知直线外的一点,_____________直线和已知直线平行__________,两直线平行.同一个平面内相交直线AB∥CD距离处处相等有且仅有一条同位角相等谢谢!
相交线与平行线7.3 平行线冀教版数学七年级下册1.理解平行的概念,掌握两条平行线间的距离处处相等.(重点)
2.掌握有关平行线的两个基本事实.(难点)学习目标情境引入问题1 在同一个平面内,两条直线的位置关系有几种可能? 温故知新相交或不相交定义 在同一平面内,不相交的两条直线叫做平行线.问题2 两条直线AB与CD相交于点O,若∠AOC=90°,那么直线AB与CD有怎样的位置关系?如何表示?AB⊥CD想一想 如果两条直线平行,如何表示呢?AB垂直于CDAB∥CDa∥ b直线AB平行于直线CD,或直线AB与CD平行直线a平行于直线b,或直线a与b平行下列说法中正确的是( )
A.如果同一平面内的两条线段不相交,那么这两条线所在直线互相平行
B.不相交的两条直线一定是平行线
C.同一平面内两条射线不相交,则这两条射线互相平行
D.同一平面内有两条直线不相交,这两条直线一定是平行线 练一练D平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件;
(2)“不相交”就是说两条直线没有交点;
(3)平行线指的是“两条直线”而不是两条射线或两条线段.方法归纳AM=BN 合作探究如图,直线a∥b. A,B为直线a上任意两点.问题1 请用三角尺分别画出点A和点B到直线b的垂线段AM,BN,观察并度量AM和BN,看看它们的长度有什么关系? M N 问题2 在直线a上另取一点C,画出点C到直线b的垂线段,它的长度与AM,BN的长度相等吗? M N Q CQ=AM=BN若直线a∥b,则直线a上任意一点到直线b的距离都相等.这个距离就叫做的平行线a与b之间的距离.两条平行线之间的距离处处相等.1.平行线之间的距离是指( )
A.从一条直线上一点到另一直线的垂线段
B.从一条直线上一点到另一条直线的垂线段长度
C.从一条直线上一点到另一条直线的垂线的长度
D.从一条直线上一点到另一条直线上的一点间线段的长度 练一练B2.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
A.2cm B.6cm C.8cm D.2cm或8cm 解析:如图1,直线a和b之间的距离为:5-3=2(cm);
如图2,直线a和b之间的距离为:5+3=8(cm).故选DD观察与思考问题1 已知直线a,如何画出另一条直线b,使它与直线a平行? b问题2 如果直线a外任意取一点C,例能过点C画出与直线a平行的直线吗?这样的直线能画出多少条? a1条基本事实 经过直线外一点,有且只有一条直线和已知直线平行.问题3 如图,只要哪对角相等,就可使a∥b? 基本事实 同位角相等,两直线平行.典例精析例 如图,∠1=55°,∠2=55°.直线a与b平行吗?为什么? 解:a∥b.理由是:因为 ∠1=55°,∠2=55°,(已知)所以 ∠1=∠2(等量代换).所以 a∥b (同位角相等,两直线平行).在对命题进行说理的过程中,经常会使用“因为”“所以”两个词,未简单起见,今后我们用符号“∵”表示“因为”,用“∴”表示“所以”.当堂练习2.已知直线a∥b∥c,a与b的距离为5cm,b与c的距离为2cm,则a与c的距离是( )
A.3cm B.7cm C.3cm或7cm D.以上都不对
1.如图,a∥b,下列线段中是a,b之间的距离的是( )
A.AB B.AE C.EF D.BC CC3.填空
如图,点C,D,E在同一条直线上,∠1=130°,∠3=50°,CF与AD平行吗?请将下面的说理过程补充完整;123∵∠1=130°(已知),∴∠2=__________________
(互为补角的定义).180°-∠1=50°∵∠3=50°(已知),∴∠___=∠_____(等量代换).∴_____∥_____( ).F23CFAD同位角相等,两直线平行CDABE4.填空
(1)如图1,∠C=60°,当∠ABE=————°时,就能使BE∥CD;
(2)如图2 , ∠1=120°,∠2=60°,则a____b. 图1图2∥ ABECD12ab 603c课堂小结平行线定义平行线间的距离两个基本事实在_____________,不______的两条______叫做平行线直线AB平行于直线CD,记作“__________”直线 a∥b,则直线a上任意一点到直线b的______叫做平行线a,b之间的距离两条平行线之间的距离__________经过已知直线外的一点,_____________直线和已知直线平行__________,两直线平行.同一个平面内相交直线AB∥CD距离处处相等有且仅有一条同位角相等谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
