冀教版数学七年级下册7.5 平行线的性质 第1课时 课件(22张ppt)
文档属性
| 名称 | 冀教版数学七年级下册7.5 平行线的性质 第1课时 课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 00:00:00 | ||
图片预览





文档简介
课件22张PPT。第七章
相交线与平行线7.5 平行线的性质
第1课时冀教版数学七年级下册1.理解并掌握平行四边形的性质定理.(重点)
2.理解并灵活运用平行四边形的性质定理解决有关问 题.(难点)学习目标复习引入如图,一束平行光线AB和DE射向一个水平镜面后被反射,此时∠1=∠2 , ∠3=∠4 .
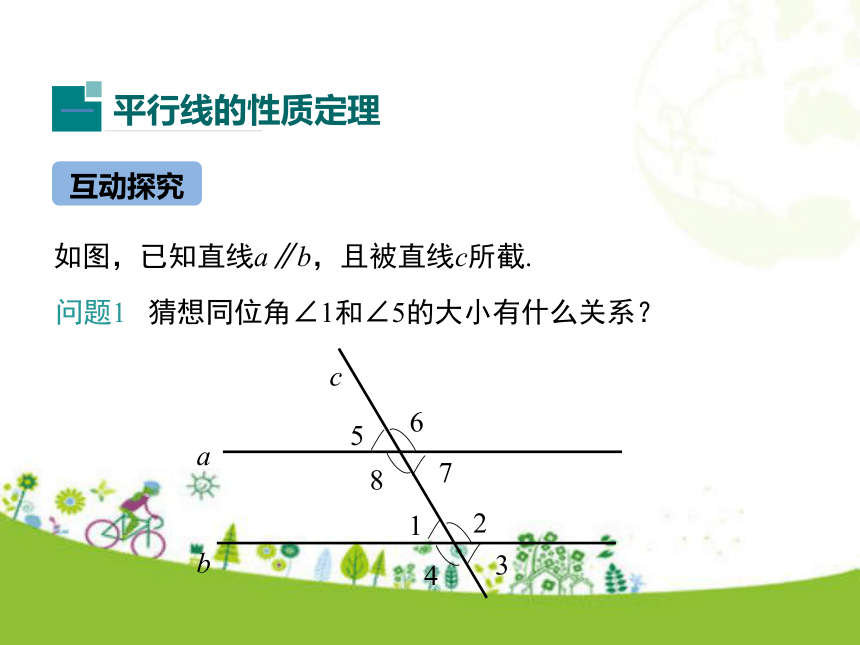
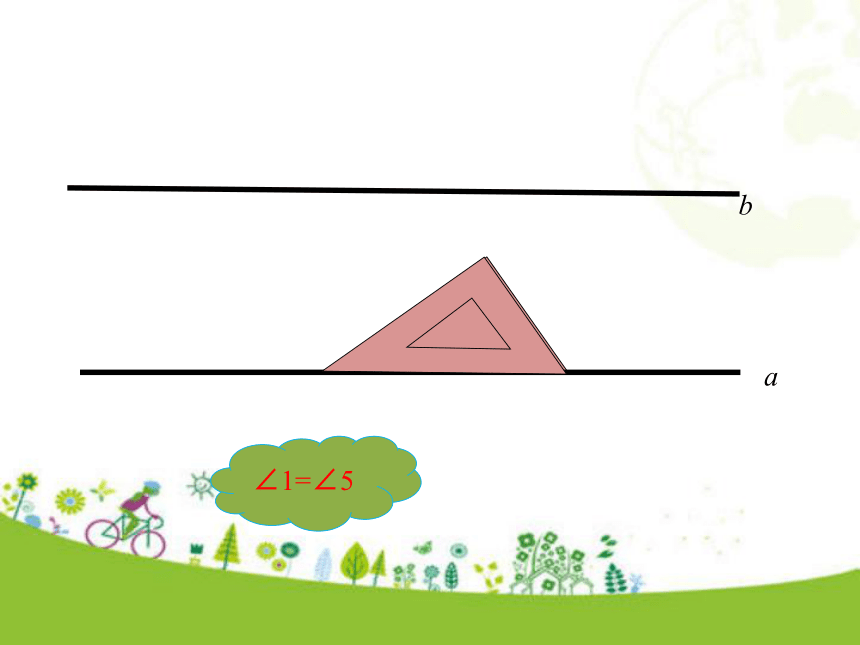
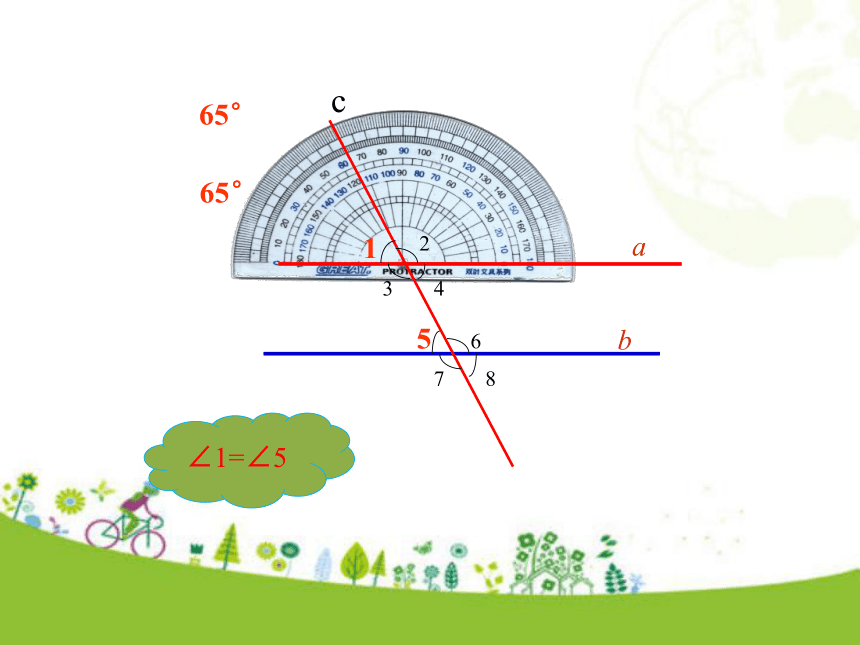
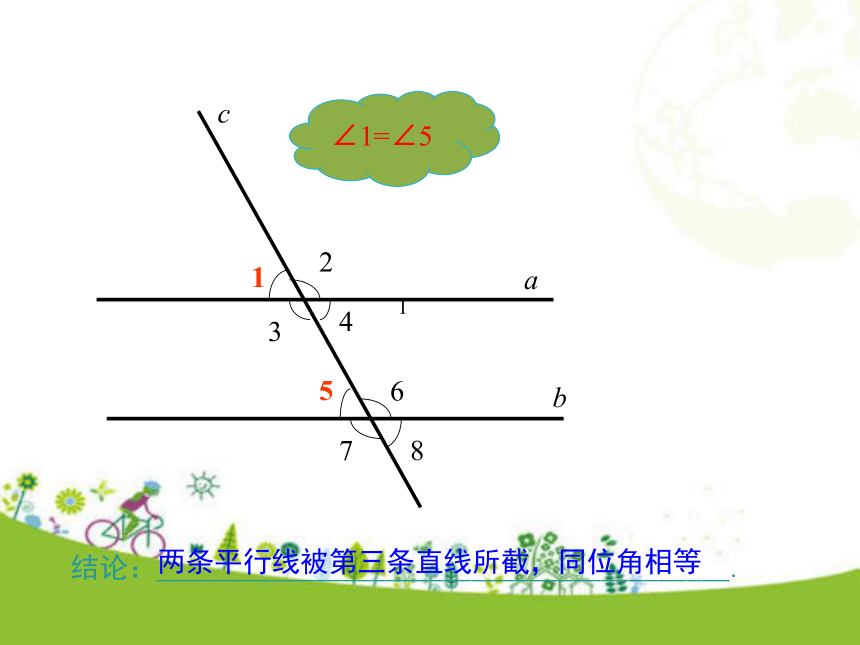
∠1,∠3的大小有什么关系?∠2与∠4呢?问题引入 如图,已知直线a∥b,且被直线c所截. 互动探究问题1 猜想同位角∠1和∠5的大小有什么关系? 65°65°cab15234678b168ac23471结论:________________________________________.两条平行线被第三条直线所截,同位角相等问题2 由∠1=∠5,能推出∠1=∠7吗?∠2与∠8也相等吗?为什么? ∠1=∠7.
理由:∵∠1=∠5(两直线平行,同位角相等),
∠5=∠7(对顶角相等),
∴ ∠1=∠7(等量代换).∠2=∠8.
理由:∵∠1=∠5(两直线平行,同位角相等),
∠2=180°-∠1,∠8=180°-∠5(补角定义),
∴ ∠2=∠8(等量代换).命题1 如图,AB∥CD,直线AB,CD被直线EF所截,则∠1=∠2.理由: ∵ AB∥CD ( ),
∴ ∠1=∠3
( ).
∵ ∠2=∠3 ( ),
∴∠1=∠2 ( ).结论:______________________.已知两直线 平行,同位角相等对顶角相等等量代换填一填两直线平行,内错角相等命题2 如图,AB∥CD,直线AB,CD被直线EF所截,则∠1+∠2=180°.理由:
∵ AB∥CD ( ),
∴ ∠1=∠3
( ) .
∵∠3+∠2=180 °( ),
∴ ∠1+∠2=180°( ).已知两直线平行,同位角相等补角定义等量代换结论:_________________________.两直线平行,同旁内角互补知识要点平行线的性质定理:
两条平行线被第三条直线所截,同位角相等.
两条平行线被第三条直线所截,内错角相等, 同旁内角互补.简称为:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.典例精析例1 已知:如图,a∥b,c∥d, ∠1=73°.求∠2和∠3的度数.解:∵a∥b (已知),
∴ ∠2=∠3(两直线平行,内错角相等).
∵ ∠1=73°(已知),
∴ ∠2=73°(等量代换).
∵c∥d (已知),
∴ ∠2+∠3=180°(两直线平行,同旁内角互补).
∴ ∠3=180°-∠2 (等式的性质).
∴ ∠3=180°-73°=107°(等量代换).如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,求∠AED的度数.练一练解:∵AB∥CD(已知),
∴∠C+∠CAB=180°
(两直线平行,同旁内角互补),
∵∠C=50°(已知),
∴∠CAB=180°-50°=130°(等式的性质).当堂练习1.两条直线被第三条直线所截,则 ( )
A.同位角相等 B.内错角互补
C.同旁内角相等 D.以上结论都不对2. 两条平行线被第三条直线所截得的角中角平分线互相垂直的是 ( )
A.内错角 B.同位角
C.同旁内角 D.以上结论都不对DC解: ∠A =∠D.理由:
∵ AB∥DE( ),
∴∠A= _______ ( ).
∵AC∥DF( ) ,
∴∠D=______ ( ).
∴∠A=∠D ( ).3.如图,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.已知∠CPE两直线平行,同位角相等已知 ∠CPE 两直线平行,同位角相等等量代换解: ∠A+∠D=180o. 理由:
∵ AB∥DE( ),
∴∠A=______ ( ).
∵AC∥DF( ),
∴∠D+ _______=180o ( ).
∴∠A+∠D=180o( ).4.如图,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。已知∠CPD两直线平行,同位角相等已知∠CPD两直线平行,同旁内角互补等量代换 5.如图,AD∥BC,AB∥DC,∠1=100°,求∠2,∠3的 度数.解:∵ AD∥BC,
∴ ∠1=∠2(两直线平行,内错角相等).
∵∠1=100°(已知),
∴ ∠2=100°.
∵ AB∥CD,
∴ ∠1+∠3=180°(两直线平行,同旁内角互补).
∵ ∠1=100°(已知),
∴ ∠3=180°-100°=80°.课堂小结平行线的性质定理两直线平行,同位角______.两直线平行,内错角______.两直线平行,同旁内角______.互补相等相等谢谢!
相交线与平行线7.5 平行线的性质
第1课时冀教版数学七年级下册1.理解并掌握平行四边形的性质定理.(重点)
2.理解并灵活运用平行四边形的性质定理解决有关问 题.(难点)学习目标复习引入如图,一束平行光线AB和DE射向一个水平镜面后被反射,此时∠1=∠2 , ∠3=∠4 .
∠1,∠3的大小有什么关系?∠2与∠4呢?问题引入 如图,已知直线a∥b,且被直线c所截. 互动探究问题1 猜想同位角∠1和∠5的大小有什么关系? 65°65°cab15234678b168ac23471结论:________________________________________.两条平行线被第三条直线所截,同位角相等问题2 由∠1=∠5,能推出∠1=∠7吗?∠2与∠8也相等吗?为什么? ∠1=∠7.
理由:∵∠1=∠5(两直线平行,同位角相等),
∠5=∠7(对顶角相等),
∴ ∠1=∠7(等量代换).∠2=∠8.
理由:∵∠1=∠5(两直线平行,同位角相等),
∠2=180°-∠1,∠8=180°-∠5(补角定义),
∴ ∠2=∠8(等量代换).命题1 如图,AB∥CD,直线AB,CD被直线EF所截,则∠1=∠2.理由: ∵ AB∥CD ( ),
∴ ∠1=∠3
( ).
∵ ∠2=∠3 ( ),
∴∠1=∠2 ( ).结论:______________________.已知两直线 平行,同位角相等对顶角相等等量代换填一填两直线平行,内错角相等命题2 如图,AB∥CD,直线AB,CD被直线EF所截,则∠1+∠2=180°.理由:
∵ AB∥CD ( ),
∴ ∠1=∠3
( ) .
∵∠3+∠2=180 °( ),
∴ ∠1+∠2=180°( ).已知两直线平行,同位角相等补角定义等量代换结论:_________________________.两直线平行,同旁内角互补知识要点平行线的性质定理:
两条平行线被第三条直线所截,同位角相等.
两条平行线被第三条直线所截,内错角相等, 同旁内角互补.简称为:两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.典例精析例1 已知:如图,a∥b,c∥d, ∠1=73°.求∠2和∠3的度数.解:∵a∥b (已知),
∴ ∠2=∠3(两直线平行,内错角相等).
∵ ∠1=73°(已知),
∴ ∠2=73°(等量代换).
∵c∥d (已知),
∴ ∠2+∠3=180°(两直线平行,同旁内角互补).
∴ ∠3=180°-∠2 (等式的性质).
∴ ∠3=180°-73°=107°(等量代换).如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,求∠AED的度数.练一练解:∵AB∥CD(已知),
∴∠C+∠CAB=180°
(两直线平行,同旁内角互补),
∵∠C=50°(已知),
∴∠CAB=180°-50°=130°(等式的性质).当堂练习1.两条直线被第三条直线所截,则 ( )
A.同位角相等 B.内错角互补
C.同旁内角相等 D.以上结论都不对2. 两条平行线被第三条直线所截得的角中角平分线互相垂直的是 ( )
A.内错角 B.同位角
C.同旁内角 D.以上结论都不对DC解: ∠A =∠D.理由:
∵ AB∥DE( ),
∴∠A= _______ ( ).
∵AC∥DF( ) ,
∴∠D=______ ( ).
∴∠A=∠D ( ).3.如图,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.已知∠CPE两直线平行,同位角相等已知 ∠CPE 两直线平行,同位角相等等量代换解: ∠A+∠D=180o. 理由:
∵ AB∥DE( ),
∴∠A=______ ( ).
∵AC∥DF( ),
∴∠D+ _______=180o ( ).
∴∠A+∠D=180o( ).4.如图,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。已知∠CPD两直线平行,同位角相等已知∠CPD两直线平行,同旁内角互补等量代换 5.如图,AD∥BC,AB∥DC,∠1=100°,求∠2,∠3的 度数.解:∵ AD∥BC,
∴ ∠1=∠2(两直线平行,内错角相等).
∵∠1=100°(已知),
∴ ∠2=100°.
∵ AB∥CD,
∴ ∠1+∠3=180°(两直线平行,同旁内角互补).
∵ ∠1=100°(已知),
∴ ∠3=180°-100°=80°.课堂小结平行线的性质定理两直线平行,同位角______.两直线平行,内错角______.两直线平行,同旁内角______.互补相等相等谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
