冀教版数学七年级下册7.5 平行线的性质 第2课时 课件(22张ppt)
文档属性
| 名称 | 冀教版数学七年级下册7.5 平行线的性质 第2课时 课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 00:00:00 | ||
图片预览







文档简介
课件22张PPT。第七章
相交线与平行线7.5 平行线的性质
第2课时冀教版数学七年级下册1.掌握平行线的判定与性质定理,能熟练运用平行线的判定与性质定理解决有关问题.(难点)
2.掌握平行于同一条直线的两条直线平行并能加以运用.(重点)学习目标复习引入情境引入理由:∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行).
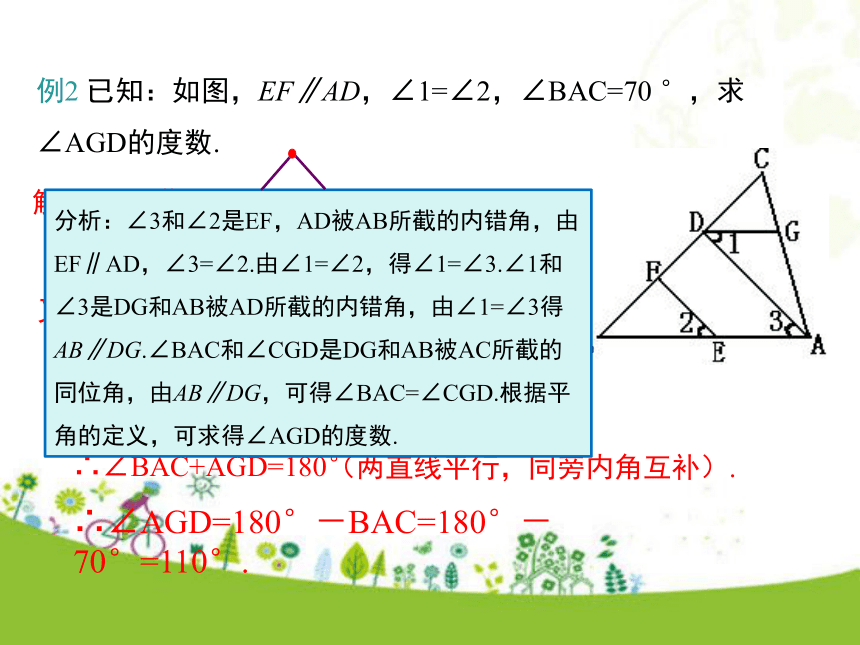
∴∠3=∠4(两直线平行,内错角相等).典例精析例1 已知:如图,∠1=∠2.对∠3=∠4说明理由.例2 已知:如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.解:∵EF∥AD(已知),∴∠2=∠3又∵∠1=∠2∴∠1=∠3∴DG∥AB∴∠BAC+AGD=180°∴∠AGD=180°-BAC=180°-70°=110°.(两直线平行,同位角相等).(已知),(等量代换).(内错角相等,两直线平行).(两直线平行,同旁内角互补).方法归纳与平行线相关的问题一般都是平行线的判定与性质的综合应用,主要体现在以下两个方面: 1. 由角定角 已知角的关系两直线平行 确定其它角的关系 2. 由线定线已知两直线平行角的关系 确定其它两直线平行判定性质判定性质1.如图所示,下列结论正确的有___________.
(把所有正确结论的序号都选上).
①若AB∥CD,则∠3=∠4;
②若∠1=∠BEG,则EF∥GH;
③若∠FGH+∠3=180°,则EF∥GH;
④若AB∥CD,∠4=62°,EG平分∠BEF,则1=59°.练一练①③④2.如图,已知:∠1=∠2,∠D=50°,求∠B的度数.解:∵∠1=∠2(已知),
∠2=∠EHD(对顶角相等),
∴∠1=∠EHD(等量代换),
∴AB∥CD(同位角相等,两直线平行).
∴∠B+∠D=180°(两直线平行,同旁内角互补).
∵∠D=50°(已知),
∴∠B=180°-50°=130°(等式的性质).互动探究 画一画:先画直线l1,再画直线l2,l3分别l1与平行.l2l1l3想一想:直线l2与l3有怎样的位置关系?l2∥ l3填一填命题3 如图,如果a∥b,a∥c,那么b∥c.理由: ∵ a∥b ( ),
∴ ∠1=∠2
( ).
∵ a∥c ( ),
∵ ∠1=∠3 ( ),
∴∠2=∠3 ( ).
∴a∥c ( ).已知两直线平行,同位角相等已知两直线平行,同位角相等等量代换同位角相等,两直线平行知识要点平行于同一条直线的两直线平行.几何语言表达:∵a // c , a // b (已知),
∴ c // b(平行于同一条直线的两直线平行).例2 已知:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数 1F分析:过点E作EF//AB, 则∠1+∠A=180°.
由AB//CD,得EF//CD,则∠C+∠FEC=180°.
由∠A=100°, ∠C=110°,可求得∠1和∠FEC的度数,根据角的和差,可求得∠AEC的度数.解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴EF//CD(平行于同一直线的两直线平行).
∴∠A+∠1=180o,∠C+∠FEC=180o
(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知)
∴∠1 =180°-∠A=80 °,
∠FEC=180°-∠C=70 ° (等式的性质)
∴∠AEC=∠1+∠FEC= 80° +70° = 150° .当堂练习1.下列推理正确的是( )A.∵a // d,b // c,∴c // d B.∵a // c,b // d,∴c // d
C.∵a // b,a // c,∴b // c D.∵a // b,c // d,∴a // cC2.直线a,b,c,d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
A.80° B.65° C.60° D.55° 3.如图,BD⊥AB,BD⊥CD,则∠a的度数是( )
A.50° B.40° C.60° D.45° BA 4.已知AB∥DE,试问∠B,∠E,∠BCE有什么关系.请完成填空: 解:过点C作CF∥AB,
则__________ ( ).
又∵AB∥DE,AB∥CF,
∴____________( ).
∴∠E=∠____( ).
∴∠B+∠E=∠1+∠2( ),
即∠B+∠E=∠BCE.CF∥DE 平行于同一直线的两条直线平行2两直线平行,内错角相等∠B=∠1两直线平行,内错角相等等式的性质5.已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.解:是.
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直的定义).
∴AD∥EG(同位角相等,两直线平行).
∴∠1=∠E(两直线平行,同位角相等), ∠2=∠3(两直线平行,内错角相等).
∵∠E=∠3(已知),
∴∠1=∠2(等量代换),
∴AD是∠BAC的平分线(角平分线的定义).6.如图,AB,CD,EF,MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,求∠1的度数.解:∵∠2=∠3=70°(已知),
∴AB∥CD(内错角相等,两直线平行),
∴∠BGP=∠GPC(两直线平行,内错角相等),
∵∠GPC=80°(已知),
∴∠BGP=80°(等量代换),
∴∠BGM=180°-∠BGP=100°(平角的定义),
∵GH平分∠MGB(已知),7.拓展提升:已知:如图,AB//CD,试解决下列问题:
(1)∠1+∠2=___ ___;
(2)∠1+∠2+∠3=___ __;
(3)∠1+∠2+∠3+∠4=_ __ __;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= ;
180°360°540°180°×(n-1)课堂小结同位角相等
内错角相等
同旁内角互补两直线平行判定性质平行于同一条直线的两条直线平行.谢谢!
相交线与平行线7.5 平行线的性质
第2课时冀教版数学七年级下册1.掌握平行线的判定与性质定理,能熟练运用平行线的判定与性质定理解决有关问题.(难点)
2.掌握平行于同一条直线的两条直线平行并能加以运用.(重点)学习目标复习引入情境引入理由:∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行).
∴∠3=∠4(两直线平行,内错角相等).典例精析例1 已知:如图,∠1=∠2.对∠3=∠4说明理由.例2 已知:如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.解:∵EF∥AD(已知),∴∠2=∠3又∵∠1=∠2∴∠1=∠3∴DG∥AB∴∠BAC+AGD=180°∴∠AGD=180°-BAC=180°-70°=110°.(两直线平行,同位角相等).(已知),(等量代换).(内错角相等,两直线平行).(两直线平行,同旁内角互补).方法归纳与平行线相关的问题一般都是平行线的判定与性质的综合应用,主要体现在以下两个方面: 1. 由角定角 已知角的关系两直线平行 确定其它角的关系 2. 由线定线已知两直线平行角的关系 确定其它两直线平行判定性质判定性质1.如图所示,下列结论正确的有___________.
(把所有正确结论的序号都选上).
①若AB∥CD,则∠3=∠4;
②若∠1=∠BEG,则EF∥GH;
③若∠FGH+∠3=180°,则EF∥GH;
④若AB∥CD,∠4=62°,EG平分∠BEF,则1=59°.练一练①③④2.如图,已知:∠1=∠2,∠D=50°,求∠B的度数.解:∵∠1=∠2(已知),
∠2=∠EHD(对顶角相等),
∴∠1=∠EHD(等量代换),
∴AB∥CD(同位角相等,两直线平行).
∴∠B+∠D=180°(两直线平行,同旁内角互补).
∵∠D=50°(已知),
∴∠B=180°-50°=130°(等式的性质).互动探究 画一画:先画直线l1,再画直线l2,l3分别l1与平行.l2l1l3想一想:直线l2与l3有怎样的位置关系?l2∥ l3填一填命题3 如图,如果a∥b,a∥c,那么b∥c.理由: ∵ a∥b ( ),
∴ ∠1=∠2
( ).
∵ a∥c ( ),
∵ ∠1=∠3 ( ),
∴∠2=∠3 ( ).
∴a∥c ( ).已知两直线平行,同位角相等已知两直线平行,同位角相等等量代换同位角相等,两直线平行知识要点平行于同一条直线的两直线平行.几何语言表达:∵a // c , a // b (已知),
∴ c // b(平行于同一条直线的两直线平行).例2 已知:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数 1F分析:过点E作EF//AB, 则∠1+∠A=180°.
由AB//CD,得EF//CD,则∠C+∠FEC=180°.
由∠A=100°, ∠C=110°,可求得∠1和∠FEC的度数,根据角的和差,可求得∠AEC的度数.解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴EF//CD(平行于同一直线的两直线平行).
∴∠A+∠1=180o,∠C+∠FEC=180o
(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知)
∴∠1 =180°-∠A=80 °,
∠FEC=180°-∠C=70 ° (等式的性质)
∴∠AEC=∠1+∠FEC= 80° +70° = 150° .当堂练习1.下列推理正确的是( )A.∵a // d,b // c,∴c // d B.∵a // c,b // d,∴c // d
C.∵a // b,a // c,∴b // c D.∵a // b,c // d,∴a // cC2.直线a,b,c,d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
A.80° B.65° C.60° D.55° 3.如图,BD⊥AB,BD⊥CD,则∠a的度数是( )
A.50° B.40° C.60° D.45° BA 4.已知AB∥DE,试问∠B,∠E,∠BCE有什么关系.请完成填空: 解:过点C作CF∥AB,
则__________ ( ).
又∵AB∥DE,AB∥CF,
∴____________( ).
∴∠E=∠____( ).
∴∠B+∠E=∠1+∠2( ),
即∠B+∠E=∠BCE.CF∥DE 平行于同一直线的两条直线平行2两直线平行,内错角相等∠B=∠1两直线平行,内错角相等等式的性质5.已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.解:是.
∵AD⊥BC,EG⊥BC(已知),
∴∠4=∠5=90°(垂直的定义).
∴AD∥EG(同位角相等,两直线平行).
∴∠1=∠E(两直线平行,同位角相等), ∠2=∠3(两直线平行,内错角相等).
∵∠E=∠3(已知),
∴∠1=∠2(等量代换),
∴AD是∠BAC的平分线(角平分线的定义).6.如图,AB,CD,EF,MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,求∠1的度数.解:∵∠2=∠3=70°(已知),
∴AB∥CD(内错角相等,两直线平行),
∴∠BGP=∠GPC(两直线平行,内错角相等),
∵∠GPC=80°(已知),
∴∠BGP=80°(等量代换),
∴∠BGM=180°-∠BGP=100°(平角的定义),
∵GH平分∠MGB(已知),7.拓展提升:已知:如图,AB//CD,试解决下列问题:
(1)∠1+∠2=___ ___;
(2)∠1+∠2+∠3=___ __;
(3)∠1+∠2+∠3+∠4=_ __ __;
(4)试探究∠1+∠2+∠3+∠4+…+∠n= ;
180°360°540°180°×(n-1)课堂小结同位角相等
内错角相等
同旁内角互补两直线平行判定性质平行于同一条直线的两条直线平行.谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
