冀教版数学七年级下册8.2 幂的乘方和积的乘方 第1课时 课件(20张ppt)
文档属性
| 名称 | 冀教版数学七年级下册8.2 幂的乘方和积的乘方 第1课时 课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 08:01:07 | ||
图片预览






文档简介
课件20张PPT。第八章
整式的乘法8.2 幂的乘方与积的乘方
第1课时冀教版数学七年级下册1.理解并掌握幂的乘方法则.(重点)
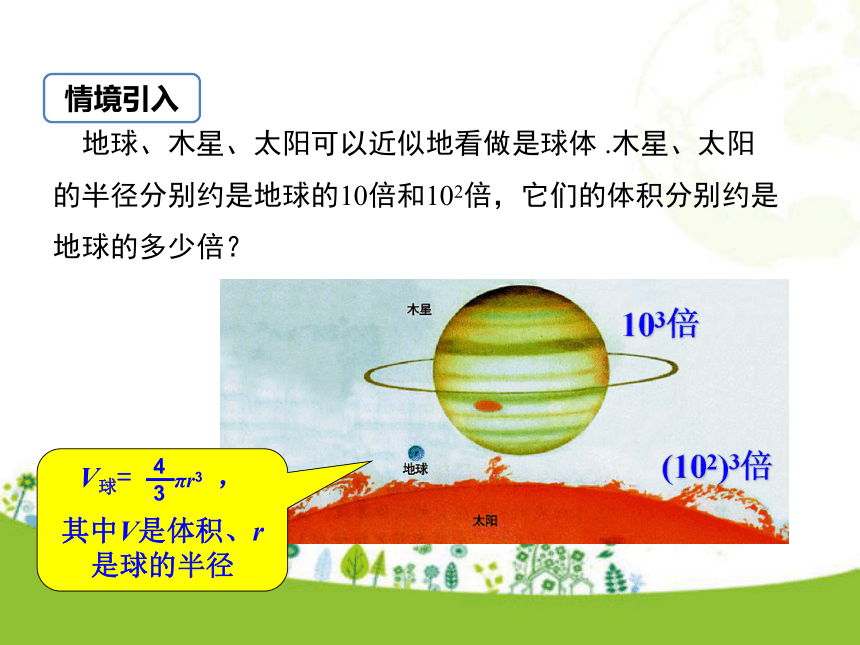
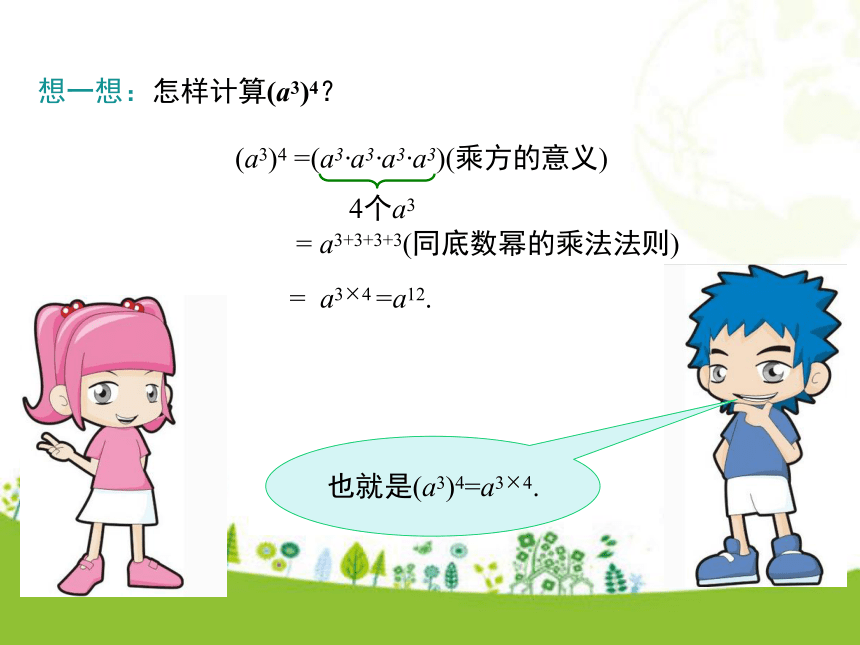
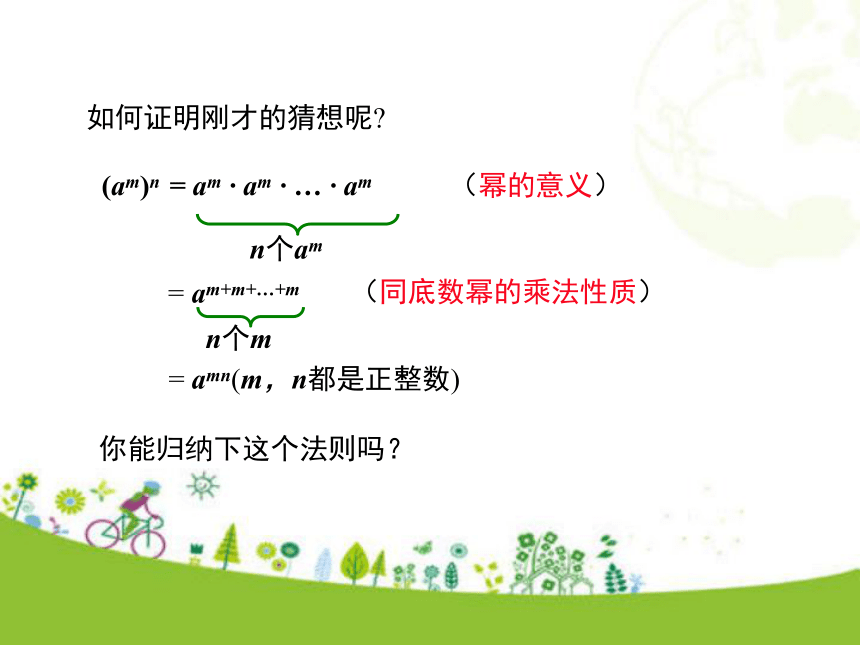
2.会运用幂的乘方法则进行幂的乘方的运算.(难点)学习目标复习引入 底数幂乘法的运算性质是什么?am · an = am+n (m、n是正整数)同底数幂相乘:底数不变,指数相加.运算形式运算方法(同底、乘法) (底不变、指加法) 地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?103倍(102)3倍情境引入互动探究 (102)3=102×102×102=102+2+2=102×3=106同底数幂的乘法性质幂的意义问题2 (102)3=106,为什么?问题1 (102)3代表什么意义?102×102×102想一想:怎样计算(a3)4?(a3)4 =(a3·a3·a3·a3)(乘方的意义)= a3+3+3+3(同底数幂的乘法法则)= a3×4 =a12. 如何证明刚才的猜想呢?(am)n = am · am · … · am= am+m+…+m= amn(m,n都是正整数) (幂的意义)(同底数幂的乘法性质)你能归纳下这个法则吗?幂的乘方法则:知识要点( am ) n = a mn (m,n是正整数).幂的乘方,底数不变,指数相乘.典例精析例1 计算:(1) (103)4; (2) (c2)3; (3) (a4)m.解:(1) (103)4=103×4=1012; (2) (c2)3=c2×3=c6; (3) (a4)m=a4×m=a4m. 例2 计算:(1) x? (x2)3;
(2) a?a2?a3-(a2)3.解:(1) x? (x2)3= x? x2×3=x? x6=x7; (2) a?a2?a3-(a2)3= a1+2+3-a2×3=a6-a6=0. 想一想:同底数幂的乘法和幂的乘方有什么共同点和不同点?am · an = am+n (m,n是正整数). ( am ) n = a mn (m,n是正整数). 1.从底数看:底数不变. (共同点)2.从指数看:同底数幂的乘法,指数相加幂的乘方,指数相乘(不同点)2)幂的乘方,底数不变,指数相乘1)同底数幂相乘,底数不变,指数相加计算:练一练=(x3)( ) =(x4)( )=x7?x( ) =x?x( )x12=(x2)( ) =(x6)( )
若 (am) n=am n=an m=(a m)n则 a mn=(a n)m6245113例如:幂的乘方的推广[(am)n]p=(amn)p=amnp(m,n,p为正整数)同样:am+n = am · an (m,n都是正整数). 例:公式的逆向运用当堂练习 1. 判断下面计算是否正确?如果不对,怎样改正? (1) (x3)3 = x6 ; (2)(104)3= 107 ; (3)a6 · a4 = a24 ;(4)(x2)3 ·(-x)2 = -x82. 填空: (1)(104)3= ;(2)(a3)3= ;
(3)-(x3)6= ;
(4)(x2)3 ·(-x)3= . 1012a9x18- x9应该是:x9 应该是:1012 应该是:a10 应该是:x8××××⑶ (a2)5 =1016=x4m=a10=221=x18=(a+b)83.计算:⑴ (104)4⑵ (xm)4(m是正整数)⑷ (23)7 ⑸ (x3)6 ⑹ [(a+b)2]4
4.计算: (2) (- x2)3 =(1)(-x3)2= x3×2= x6(3) -(y2)3=-y 2×3=-y6-x2×3=-x6(4) –(y 3)2 = – y6=-y 3×2注意符号解:5.计算:(1) x2·x4+(x3)2; 解:x2·x4+(x3)2
=x2+4 + x3×2
=x6+x6
=2x6;(2) (a3)3·(a4)3能力提升:已知 44×83=2x,求x的值.解:∵44×83= (22)4×(23)3= 28×29= 217∴x=17.课堂小结幂的乘方法则(am)n=amn (m,n是正整数)注意幂的乘方,底数不变,指数相乘幂的乘方与同底数幂的乘法的区别:(am)n=amn; am ﹒an=am+n幂的乘方法则的逆用:
amn=(am)n=(an)m谢谢!
整式的乘法8.2 幂的乘方与积的乘方
第1课时冀教版数学七年级下册1.理解并掌握幂的乘方法则.(重点)
2.会运用幂的乘方法则进行幂的乘方的运算.(难点)学习目标复习引入 底数幂乘法的运算性质是什么?am · an = am+n (m、n是正整数)同底数幂相乘:底数不变,指数相加.运算形式运算方法(同底、乘法) (底不变、指加法) 地球、木星、太阳可以近似地看做是球体 .木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?103倍(102)3倍情境引入互动探究 (102)3=102×102×102=102+2+2=102×3=106同底数幂的乘法性质幂的意义问题2 (102)3=106,为什么?问题1 (102)3代表什么意义?102×102×102想一想:怎样计算(a3)4?(a3)4 =(a3·a3·a3·a3)(乘方的意义)= a3+3+3+3(同底数幂的乘法法则)= a3×4 =a12. 如何证明刚才的猜想呢?(am)n = am · am · … · am= am+m+…+m= amn(m,n都是正整数) (幂的意义)(同底数幂的乘法性质)你能归纳下这个法则吗?幂的乘方法则:知识要点( am ) n = a mn (m,n是正整数).幂的乘方,底数不变,指数相乘.典例精析例1 计算:(1) (103)4; (2) (c2)3; (3) (a4)m.解:(1) (103)4=103×4=1012; (2) (c2)3=c2×3=c6; (3) (a4)m=a4×m=a4m. 例2 计算:(1) x? (x2)3;
(2) a?a2?a3-(a2)3.解:(1) x? (x2)3= x? x2×3=x? x6=x7; (2) a?a2?a3-(a2)3= a1+2+3-a2×3=a6-a6=0. 想一想:同底数幂的乘法和幂的乘方有什么共同点和不同点?am · an = am+n (m,n是正整数). ( am ) n = a mn (m,n是正整数). 1.从底数看:底数不变. (共同点)2.从指数看:同底数幂的乘法,指数相加幂的乘方,指数相乘(不同点)2)幂的乘方,底数不变,指数相乘1)同底数幂相乘,底数不变,指数相加计算:练一练=(x3)( ) =(x4)( )=x7?x( ) =x?x( )x12=(x2)( ) =(x6)( )
若 (am) n=am n=an m=(a m)n则 a mn=(a n)m6245113例如:幂的乘方的推广[(am)n]p=(amn)p=amnp(m,n,p为正整数)同样:am+n = am · an (m,n都是正整数). 例:公式的逆向运用当堂练习 1. 判断下面计算是否正确?如果不对,怎样改正? (1) (x3)3 = x6 ; (2)(104)3= 107 ; (3)a6 · a4 = a24 ;(4)(x2)3 ·(-x)2 = -x82. 填空: (1)(104)3= ;(2)(a3)3= ;
(3)-(x3)6= ;
(4)(x2)3 ·(-x)3= . 1012a9x18- x9应该是:x9 应该是:1012 应该是:a10 应该是:x8××××⑶ (a2)5 =1016=x4m=a10=221=x18=(a+b)83.计算:⑴ (104)4⑵ (xm)4(m是正整数)⑷ (23)7 ⑸ (x3)6 ⑹ [(a+b)2]4
4.计算: (2) (- x2)3 =(1)(-x3)2= x3×2= x6(3) -(y2)3=-y 2×3=-y6-x2×3=-x6(4) –(y 3)2 = – y6=-y 3×2注意符号解:5.计算:(1) x2·x4+(x3)2; 解:x2·x4+(x3)2
=x2+4 + x3×2
=x6+x6
=2x6;(2) (a3)3·(a4)3能力提升:已知 44×83=2x,求x的值.解:∵44×83= (22)4×(23)3= 28×29= 217∴x=17.课堂小结幂的乘方法则(am)n=amn (m,n是正整数)注意幂的乘方,底数不变,指数相乘幂的乘方与同底数幂的乘法的区别:(am)n=amn; am ﹒an=am+n幂的乘方法则的逆用:
amn=(am)n=(an)m谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
