冀教版数学七年级下册8.2 幂的乘方和积的乘方 第2课时 课件(22张ppt)
文档属性
| 名称 | 冀教版数学七年级下册8.2 幂的乘方和积的乘方 第2课时 课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 00:00:00 | ||
图片预览








文档简介
课件22张PPT。第八章
整式的乘法8.2 幂的乘方与积的乘方
第2课时冀教版数学七年级下册1.理解并掌握积的乘方法则及其应用.(重点)
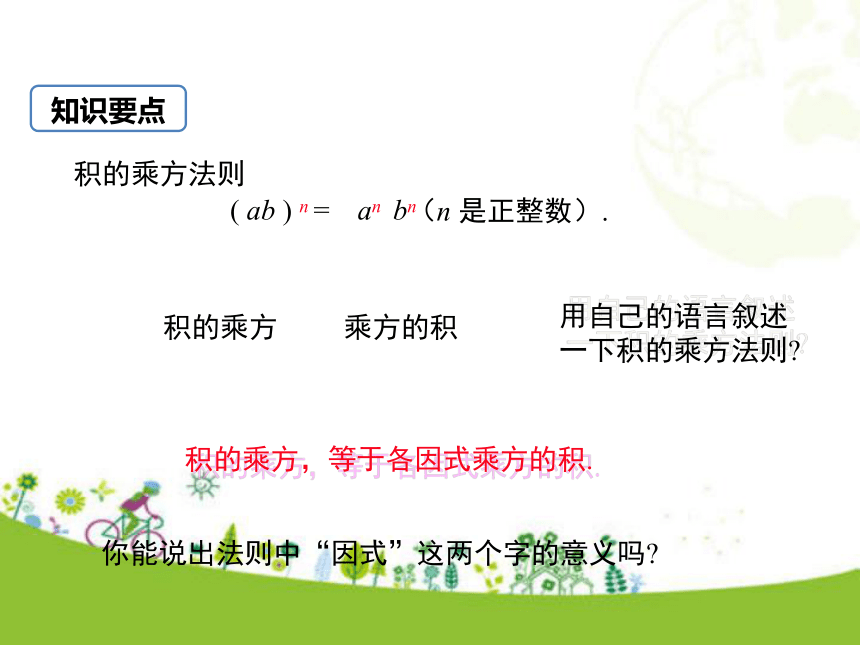
2.会运用积的乘方的运算法则进行计算.(难点)学习目标复习引入 同底数幂相乘法则是什么?幂的乘方运算法则?即:am · an = am+n (m,n都是正整数). 即:( am ) n = a mn(m,n都是正整数).2)幂的乘方,底数不变,指数相乘1)同底数幂相乘,底数不变,指数相加底数不变指数相乘指数相加其中m , n都是正整数(am)n=amnam·an=am+n想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?自主探究思考下面两道题:(1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.这两道题有什么特点?底数为两个因式相乘,积的形式.这种形式为积的乘方我们学过的幂的乘方的运算性质适用吗?同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则) 把上面的运算过程推广到一般情况,即 (ab)n = (ab) · (ab) · … · (ab)= (a · a · … ·a ) · (b · b · … ·b)= anbn (a为正整数). 想一想:怎样计算(ab)n ?在运算过程中你用到了哪些知识?(幂的意义)(乘法交换律和结合律)(幂的意义)积的乘方 乘方的积( ab ) n = an bn(n 是正整数).积的乘方法则用自己的语言叙述一下积的乘方法则? 积的乘方,等于各因式乘方的积.你能说出法则中“因式”这两个字的意义吗? 知识要点典例精析例1 计算:答:地球的表面积大约是5.10×1014m2.(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2. 解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;解:原式=9x2y4 +4x2y4
=13x2y4;解:原式= -8x9·x4 =-8x13. 注意:运算顺序是
先乘方,再乘除,
最后算加减.计算:练一练( abc )n=an · bn · cn想一想:三个或三个以上的积的乘方,是否也具有上面的性质? 怎样用公式表示? (abc)n = (abc)·(abc) … ·(abc) =(a · a… ·a)·(b · b … ·b) ·(c · c … ·c) = anbncn练一练计算: -( xyz )4 + ( 2x2y2z2 )2.解: -(xyz )4 + (2x2y2z2 )2 an·bn = (ab)n (ab)n=an·bn 逆运用解:(1) 23×53 = (2×5)3 = 103. (2) 28×58= (2×5)8 = 108. (3) (-5)16 × (-2)15= (-5)×[(-5)×(-2)]15= -5×1015 . (4) 24 × 44 ×(-0.125)4 = [2×4×(-0.125)]4= 14= 1 . 当堂练习(1)(ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )1.判断: 2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4C3. (0.04)2013×[(-5)2013]2=________.你有几种解法?1 (1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3.3.计算: 解:(1)原式=a8·b8;(2)原式= 23 ·m3=8m3;(3)原式=(-x)5 ·y5=-x5y5;(4)原式=53 ·a3 ·(b2)3=125 a3 b6;(5)原式=22 ×(102)2=4 ×104;(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
1.-2(a2)3 · (a3)2 · a -(-a)2 ·(-a)3 · (a4)2.解: -2(a2)3 · (a3)2 · a-(-a)2 ·(-a)3 · (a4)2
= -2a6 · a6 · a –a2 ·(-a)3 ·a8
= -2a6+6+1 + a2+3+8
= -2a13+a13
= -a13.4.计算: 2. 2(-a)2 · (b2)3 -3a2 ·(-b3)2.解:2(-a)2 · (b2)3 -3a2 ·(-b3)2= 2a2b6 -3a2b6= -a2b6.能力提升:如果(an?bm?b)3=a9b15,求m, n的值.? (an)3?(bm)3?b3=a9b15,? a 3n ?b 3m?b3=a9b15 ,? a 3n ?b 3m+3=a9b15,? 3n=9 ,3m+3=15.?n=3,m=4.解: ∵(an?bm?b)3=a9b15,课堂小结积的乘方法则 (ab)n=anbn ( n是正整数)反向运用
an·bn = (ab)n注意运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)谢谢!
整式的乘法8.2 幂的乘方与积的乘方
第2课时冀教版数学七年级下册1.理解并掌握积的乘方法则及其应用.(重点)
2.会运用积的乘方的运算法则进行计算.(难点)学习目标复习引入 同底数幂相乘法则是什么?幂的乘方运算法则?即:am · an = am+n (m,n都是正整数). 即:( am ) n = a mn(m,n都是正整数).2)幂的乘方,底数不变,指数相乘1)同底数幂相乘,底数不变,指数相加底数不变指数相乘指数相加其中m , n都是正整数(am)n=amnam·an=am+n想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?自主探究思考下面两道题:(1)(2)我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.这两道题有什么特点?底数为两个因式相乘,积的形式.这种形式为积的乘方我们学过的幂的乘方的运算性质适用吗?同理:(乘方的意义)(乘法交换律、结合律)(同底数幂相乘的法则) 把上面的运算过程推广到一般情况,即 (ab)n = (ab) · (ab) · … · (ab)= (a · a · … ·a ) · (b · b · … ·b)= anbn (a为正整数). 想一想:怎样计算(ab)n ?在运算过程中你用到了哪些知识?(幂的意义)(乘法交换律和结合律)(幂的意义)积的乘方 乘方的积( ab ) n = an bn(n 是正整数).积的乘方法则用自己的语言叙述一下积的乘方法则? 积的乘方,等于各因式乘方的积.你能说出法则中“因式”这两个字的意义吗? 知识要点典例精析例1 计算:答:地球的表面积大约是5.10×1014m2.(1) 2(x3)2·x3-(3x3)3+(5x)2·x7;
(2)(3xy2)2+(-4xy3) · (-xy) ;
(3)(-2x3)3·(x2)2. 解:原式=2x6·x3-27x9+25x2·x7
= 2x9-27x9+25x9 = 0;解:原式=9x2y4 +4x2y4
=13x2y4;解:原式= -8x9·x4 =-8x13. 注意:运算顺序是
先乘方,再乘除,
最后算加减.计算:练一练( abc )n=an · bn · cn想一想:三个或三个以上的积的乘方,是否也具有上面的性质? 怎样用公式表示? (abc)n = (abc)·(abc) … ·(abc) =(a · a… ·a)·(b · b … ·b) ·(c · c … ·c) = anbncn练一练计算: -( xyz )4 + ( 2x2y2z2 )2.解: -(xyz )4 + (2x2y2z2 )2 an·bn = (ab)n (ab)n=an·bn 逆运用解:(1) 23×53 = (2×5)3 = 103. (2) 28×58= (2×5)8 = 108. (3) (-5)16 × (-2)15= (-5)×[(-5)×(-2)]15= -5×1015 . (4) 24 × 44 ×(-0.125)4 = [2×4×(-0.125)]4= 14= 1 . 当堂练习(1)(ab2)3=ab6 ( ) ×××(2) (3xy)3=9x3y3 ( ) ×(3) (-2a2)2=-4a4 ( )(4) -(-ab2)2=a2b4 ( )1.判断: 2.下列运算正确的是( )
A. x.x2=x2 B. (xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4C3. (0.04)2013×[(-5)2013]2=________.你有几种解法?1 (1) (ab)8 ; (2) (2m)3 ; (3) (-xy)5;
(4) (5ab2)3 ; (5) (2×102)2 ; (6) (-3×103)3.3.计算: 解:(1)原式=a8·b8;(2)原式= 23 ·m3=8m3;(3)原式=(-x)5 ·y5=-x5y5;(4)原式=53 ·a3 ·(b2)3=125 a3 b6;(5)原式=22 ×(102)2=4 ×104;(6)原式=(-3)3 ×(103)3=-27 ×109=-2.7 ×1010.
1.-2(a2)3 · (a3)2 · a -(-a)2 ·(-a)3 · (a4)2.解: -2(a2)3 · (a3)2 · a-(-a)2 ·(-a)3 · (a4)2
= -2a6 · a6 · a –a2 ·(-a)3 ·a8
= -2a6+6+1 + a2+3+8
= -2a13+a13
= -a13.4.计算: 2. 2(-a)2 · (b2)3 -3a2 ·(-b3)2.解:2(-a)2 · (b2)3 -3a2 ·(-b3)2= 2a2b6 -3a2b6= -a2b6.能力提升:如果(an?bm?b)3=a9b15,求m, n的值.? (an)3?(bm)3?b3=a9b15,? a 3n ?b 3m?b3=a9b15 ,? a 3n ?b 3m+3=a9b15,? 3n=9 ,3m+3=15.?n=3,m=4.解: ∵(an?bm?b)3=a9b15,课堂小结积的乘方法则 (ab)n=anbn ( n是正整数)反向运用
an·bn = (ab)n注意运用积的乘方法则时要注意:
公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
