冀教版数学七年级下册8.4 整式的乘法 第1课时 课件(18张ppt)
文档属性
| 名称 | 冀教版数学七年级下册8.4 整式的乘法 第1课时 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 08:03:24 | ||
图片预览






文档简介
课件18张PPT。第八章
整式的乘法8.4 整式的乘法
第1课时冀教版数学七年级下册1.掌握单项式与单项式相乘的运算法则.(重点)
2.能够灵活地进行单项式与单项式相乘的运算.(难点)学习目标复习引入1.幂的运算性质有哪几条? 同底数幂的乘法法则:am·an=am+n ( m、n都是正整数).幂的乘方法则:(am)n=amn ( m、n都是正整数).积的乘方法则:(ab)n=anbn ( m、n都是正整数).2.计算:(1)x2 · x3 · x4= ; (2)(x3)6= ;
(3)(-2a4b2)3= ; (4) (a2)3 · a4= ;
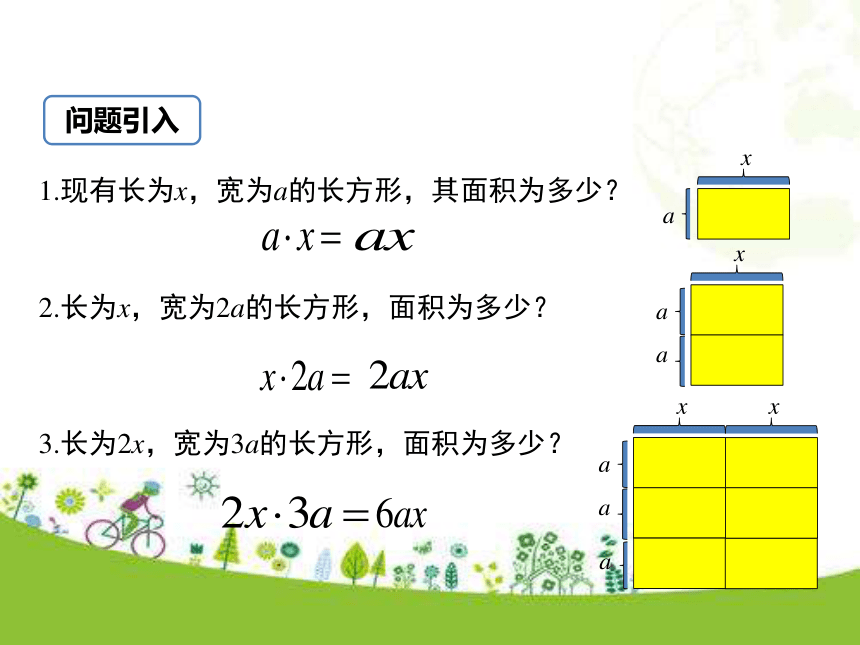
(5) .x9x18-8a12b6a101问题引入1.现有长为x,宽为a的长方形,其面积为多少? 2.长为x,宽为2a的长方形,面积为多少?3.长为2x,宽为3a的长方形,面积为多少?观察与思考问题 光的速度约为3×105km/s,太阳光照射到地球上需要的时间大约是5×102s,你知道地球与太阳的距离约是多少千米吗?地球与太阳的距离约是(3×105)×(5×102)km(1)利用乘法交换律和结合律有:(3×105)×(5×102)=(3×5)×(105×102)=15×107.想一想:怎样计算(3 ×105)×(5 ×102)?计算过程中用到了哪些运算律及运算性质?如果将上式中的数字改为字母,比如2ac5 ·3bc2,怎样计算这个式子?(2) 2ac5 ·3bc2=(2×3)(a ·b) ·(c5·c2) (乘法交换律、结合律)
=6abc5+2 (同底数幂的乘法)
=6abc7. 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它们的指数作为积的一个因式.知识要点单项式与单项式相乘典例精析例1 计算:单项式相乘的结果仍是单项式单独因式y别漏乘漏写比一比:看谁做的又快又准!例2 计算:有积的乘方怎么办?运算时应先算什么?单项式乘以单项式中的“一、二、三”
一个不变:单项式与单项式相乘时,对于只在一个单项式里含有的字母,连同它的指数不变,作为积的因式.
二个相乘:把各个单项式中的系数、相同字母的幂分别相乘.归纳总结三个检验:单项式乘以单项式的结果是否正确,可从以下三个方面来检验:
①结果仍是单项式;
②结果中含有单项式中的所有字母;
③结果中每一个字母的指数都等于前面单项式中
同一字母的指数和.当堂练习1.下面计算结果对不对?如果不对,应当怎样改正?
(1)3a3 ·2a2=6a6 ( ) 改正: .
(2) 2x2 ·3x2=6x4 ( ) 改正: .
(3)3x2 ·4x2=12x2 ( ) 改正: .
(4) 5y3·3y5=15y15 ( ) 改正: .3a3 ·2a2=6a5 3x2 ·4x2=12x4 5y3·3y5=15y8 ×××2.计算:(1) 3x2 ·5x3 ; (2)4y ·(-2xy2);(3) (-3x)2 ·4x2 ; (4)(-2a)3(-3a)2解: 原式=(3×5)(x2·x3)
=15x5;解: 原式=[4×(-2)](y·y2) ·x
=-8xy3;解: 原式=9x2·4x2
=(9×4)(x2·x2)
=36x4;
解: 原式=-8a3·9a2
=[(-8)×9](a3·a2)
=-72a53.填空:
(1)若长方形的宽是a2,长是宽的2倍,则长方形的面积为_____.
(2)一个三角形的一边长为a,这条边上的高的长度是它的 那么这个三角形的面积是_____.2a4(2)若n为正整数,且x3n=2,求2x2n ·x4n+x4n ·x5n的值.解: 2x2n ·x4n+x4n ·x5n
=2x6n+x9n=2(x3n)2+(x3n)3
=2×22+23=16
∴原式的值等于16. 4.计算:
(1) (-5a2b)· (-3a) · (-2ab2c)解:原式= [(-5)×(-3)×(-2)] (a2·a·a)(b·b2)·c
= -30 a4 b3 c课堂小结单项式乘以单项式运算法则注意事项实质上是转化为同底数幂的运算计算时要注意符号问题单独的字母不要漏写漏乘有乘方时,先算乘方谢谢!
整式的乘法8.4 整式的乘法
第1课时冀教版数学七年级下册1.掌握单项式与单项式相乘的运算法则.(重点)
2.能够灵活地进行单项式与单项式相乘的运算.(难点)学习目标复习引入1.幂的运算性质有哪几条? 同底数幂的乘法法则:am·an=am+n ( m、n都是正整数).幂的乘方法则:(am)n=amn ( m、n都是正整数).积的乘方法则:(ab)n=anbn ( m、n都是正整数).2.计算:(1)x2 · x3 · x4= ; (2)(x3)6= ;
(3)(-2a4b2)3= ; (4) (a2)3 · a4= ;
(5) .x9x18-8a12b6a101问题引入1.现有长为x,宽为a的长方形,其面积为多少? 2.长为x,宽为2a的长方形,面积为多少?3.长为2x,宽为3a的长方形,面积为多少?观察与思考问题 光的速度约为3×105km/s,太阳光照射到地球上需要的时间大约是5×102s,你知道地球与太阳的距离约是多少千米吗?地球与太阳的距离约是(3×105)×(5×102)km(1)利用乘法交换律和结合律有:(3×105)×(5×102)=(3×5)×(105×102)=15×107.想一想:怎样计算(3 ×105)×(5 ×102)?计算过程中用到了哪些运算律及运算性质?如果将上式中的数字改为字母,比如2ac5 ·3bc2,怎样计算这个式子?(2) 2ac5 ·3bc2=(2×3)(a ·b) ·(c5·c2) (乘法交换律、结合律)
=6abc5+2 (同底数幂的乘法)
=6abc7. 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它们的指数作为积的一个因式.知识要点单项式与单项式相乘典例精析例1 计算:单项式相乘的结果仍是单项式单独因式y别漏乘漏写比一比:看谁做的又快又准!例2 计算:有积的乘方怎么办?运算时应先算什么?单项式乘以单项式中的“一、二、三”
一个不变:单项式与单项式相乘时,对于只在一个单项式里含有的字母,连同它的指数不变,作为积的因式.
二个相乘:把各个单项式中的系数、相同字母的幂分别相乘.归纳总结三个检验:单项式乘以单项式的结果是否正确,可从以下三个方面来检验:
①结果仍是单项式;
②结果中含有单项式中的所有字母;
③结果中每一个字母的指数都等于前面单项式中
同一字母的指数和.当堂练习1.下面计算结果对不对?如果不对,应当怎样改正?
(1)3a3 ·2a2=6a6 ( ) 改正: .
(2) 2x2 ·3x2=6x4 ( ) 改正: .
(3)3x2 ·4x2=12x2 ( ) 改正: .
(4) 5y3·3y5=15y15 ( ) 改正: .3a3 ·2a2=6a5 3x2 ·4x2=12x4 5y3·3y5=15y8 ×××2.计算:(1) 3x2 ·5x3 ; (2)4y ·(-2xy2);(3) (-3x)2 ·4x2 ; (4)(-2a)3(-3a)2解: 原式=(3×5)(x2·x3)
=15x5;解: 原式=[4×(-2)](y·y2) ·x
=-8xy3;解: 原式=9x2·4x2
=(9×4)(x2·x2)
=36x4;
解: 原式=-8a3·9a2
=[(-8)×9](a3·a2)
=-72a53.填空:
(1)若长方形的宽是a2,长是宽的2倍,则长方形的面积为_____.
(2)一个三角形的一边长为a,这条边上的高的长度是它的 那么这个三角形的面积是_____.2a4(2)若n为正整数,且x3n=2,求2x2n ·x4n+x4n ·x5n的值.解: 2x2n ·x4n+x4n ·x5n
=2x6n+x9n=2(x3n)2+(x3n)3
=2×22+23=16
∴原式的值等于16. 4.计算:
(1) (-5a2b)· (-3a) · (-2ab2c)解:原式= [(-5)×(-3)×(-2)] (a2·a·a)(b·b2)·c
= -30 a4 b3 c课堂小结单项式乘以单项式运算法则注意事项实质上是转化为同底数幂的运算计算时要注意符号问题单独的字母不要漏写漏乘有乘方时,先算乘方谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
