冀教版数学七年级下册8.4 整式的乘法 第3课时 课件(21张ppt)
文档属性
| 名称 | 冀教版数学七年级下册8.4 整式的乘法 第3课时 课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 00:00:00 | ||
图片预览








文档简介
课件21张PPT。第八章
整式的乘法8.4 整式的乘法
第3课时冀教版数学七年级下册1.理解并掌握多项式与多项式的乘法运算法则.(重点)
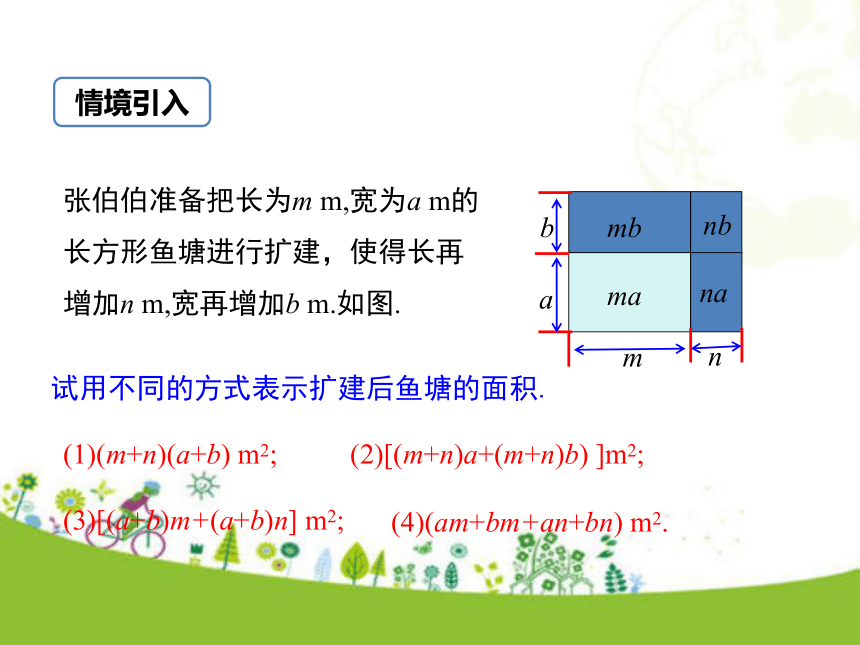
2.能够多项式与多项式的乘法运算法则进行计算.(难点)学习目标复习引入1.如何进行单项式与多项式乘法的运算?② 再把积相加.① 将单项式分别乘以多项式的每一项2.进行单项式与多项式乘法运算时,要注意什么?① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.情境引入张伯伯准备把长为m m,宽为a m的长方形鱼塘进行扩建,使得长再增加n m,宽再增加b m.如图.mbmanbna试用不同的方式表示扩建后鱼塘的面积.(1)(m+n)(a+b) m2;(2)[(m+n)a+(m+n)b) ]m2;(3)[(a+b)m+(a+b)n] m2;(4)(am+bm+an+bn) m2.互动探究 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= (m+n)a+(m+n)b 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am1234+an+bm+bn多乘多顺口溜:多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.知识要点多项式乘多项式典例精析例1 计算:解:多项式乘以多项式的“三点注意”
(1)一定要按照一定的顺序相乘,做到不重不漏.
(2)计算时,一定要注意符号问题,每一项都包含前面的符号.
(3)如果结果中有同类项,一定要合并同类项.归纳总结例2 计算:解:练一练判断下列解法是否正确,若错,请说出理由.漏乘当堂练习1.(x-1)(2x+3)的计算结果是( )
A.2x2+x-3 B.2x2-x-3
C.2x2-x+3 D.x3-2x-3A2.若(x+4)(x-3)=x2+mx-n,则( )
A.m=-1,n=12 B.m=-1,n=-12
C.m=1,n=-12 D.m=1,n=12解析:因为(x+4)(x-3)=x2+x-12=x2+mx-n,所以m=1,n=12.故选D.D3.计算:
(1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).解:(1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y; (3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.4.解方程:8x2-(2x-3)(4x+2)=14.解:8x2-(2x-3)(4x+2)=14,
8x2-(8x2+4x-12x-6)=14,
8x2-8x2-4x+12x+6=14,
8x=8,
x=1.5.计算求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.解:原式=当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2=22+14 -56
=-20. 观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.5 6(-3) (-4)2 (-8)(-5) 6口答:6.计算(-2) (-35)能力提升: 小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,问小东应在挂历画上裁下一块多大面积的长方形?面积:(2m+2b+c)(2m+a)解:(2m+2b+c)(2m+a)= 4m2+2ma+4bm+2ab+2cm+ca.答:小东应在挂历画上裁下一(4m2+2ma+4bm+2ab+2cm
+ca)平方厘米的长方形.课堂小结多项式乘多项式运算法则
注意事项不要漏乘;正确确定各符号;结果要最简 实质上是转化为单项式乘多项式的运算(x-1)2在一般情况下不等于x2-12.谢谢!
整式的乘法8.4 整式的乘法
第3课时冀教版数学七年级下册1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够多项式与多项式的乘法运算法则进行计算.(难点)学习目标复习引入1.如何进行单项式与多项式乘法的运算?② 再把积相加.① 将单项式分别乘以多项式的每一项2.进行单项式与多项式乘法运算时,要注意什么?① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.情境引入张伯伯准备把长为m m,宽为a m的长方形鱼塘进行扩建,使得长再增加n m,宽再增加b m.如图.mbmanbna试用不同的方式表示扩建后鱼塘的面积.(1)(m+n)(a+b) m2;(2)[(m+n)a+(m+n)b) ]m2;(3)[(a+b)m+(a+b)n] m2;(4)(am+bm+an+bn) m2.互动探究 由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有
(m+n)(a+b)=ma+ mb+ na+ nb如何进行多项式与多项式相乘的运算 ?实际上,把(m+n)看成一个整体,有:= ma+mb+na+nb(m+n)(a+b)= (m+n)a+(m+n)b 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am1234+an+bm+bn多乘多顺口溜:多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.知识要点多项式乘多项式典例精析例1 计算:解:多项式乘以多项式的“三点注意”
(1)一定要按照一定的顺序相乘,做到不重不漏.
(2)计算时,一定要注意符号问题,每一项都包含前面的符号.
(3)如果结果中有同类项,一定要合并同类项.归纳总结例2 计算:解:练一练判断下列解法是否正确,若错,请说出理由.漏乘当堂练习1.(x-1)(2x+3)的计算结果是( )
A.2x2+x-3 B.2x2-x-3
C.2x2-x+3 D.x3-2x-3A2.若(x+4)(x-3)=x2+mx-n,则( )
A.m=-1,n=12 B.m=-1,n=-12
C.m=1,n=-12 D.m=1,n=12解析:因为(x+4)(x-3)=x2+x-12=x2+mx-n,所以m=1,n=12.故选D.D3.计算:
(1)(3x+1)(x+2); (2)(x-8)(x-y);
(3) (x+y)(x2-xy+y2).解:(1) 原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;(2) 原式=x·x-xy-8x+8y
=x2-xy-8x+8y; (3) 原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.4.解方程:8x2-(2x-3)(4x+2)=14.解:8x2-(2x-3)(4x+2)=14,
8x2-(8x2+4x-12x-6)=14,
8x2-8x2-4x+12x+6=14,
8x=8,
x=1.5.计算求值:
(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中x=1,y=-2.解:原式=当x=1,y=-2时,
原式=22×1-7×1×(-2)-14×(-2)2=22+14 -56
=-20. 观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.5 6(-3) (-4)2 (-8)(-5) 6口答:6.计算(-2) (-35)能力提升: 小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,问小东应在挂历画上裁下一块多大面积的长方形?面积:(2m+2b+c)(2m+a)解:(2m+2b+c)(2m+a)= 4m2+2ma+4bm+2ab+2cm+ca.答:小东应在挂历画上裁下一(4m2+2ma+4bm+2ab+2cm
+ca)平方厘米的长方形.课堂小结多项式乘多项式运算法则
注意事项不要漏乘;正确确定各符号;结果要最简 实质上是转化为单项式乘多项式的运算(x-1)2在一般情况下不等于x2-12.谢谢!
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
