人教版八年级数学下册:17.1 勾股定理 第1课时 课件(24张PPT)
文档属性
| 名称 | 人教版八年级数学下册:17.1 勾股定理 第1课时 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 07:23:28 | ||
图片预览



文档简介
(共24张PPT)
第十七章 勾股定理
Zx```xk
17.1 勾股定理
第1课时
学习目标:
1)探索直角三角形两条直角边的平方和与斜边的平方的关系。
2)发展合情推理能力,体会数形结合的思想.
员工廉洁从业承诺书范文选集
领导干部的廉洁自律,是反腐败三项工作的首要任务,是搞好党风廉政建设的前提和关键。下面有小编整理的,欢迎阅读!
我作为xxxxxx公司的销售人员,为了做到廉洁从业,郑重承诺如下:
1.不以任何方式泄露、透漏公司客户、管理、产品、技术、销售等商业秘密。
2.在公司产品调价信息未执行前,不以任何明示、暗示等方式向客户或他人透漏。
3.不利用公司产品销售差价与亲属、朋友及其开办的公司发生业务,不损害公司利益。
4.不贪污、侵占公司财产,不将公款私存。
5.不以公司名义挂账、赊欠。不从客户处以任何理由借款、借物。
6.不以任何形式搞虚假报销,套取出差费。
7.不虚报、谎报、挪用业务费。
8.不接受客户的现金、物品、有价证券或高规格接待。
9.不将公司赠送客户的物品或客户赠送公司的物品占为己有。
10.不以招待客户为借口,利用公款吃喝。接待客户不
铺张浪费。
11.不介入客户与公司购销业务无关的活动。
12.不从事其他兼职工作,不推销本公司经营范围以外的产品。
如发现违反上述任何一条承诺,自愿接受公司的处罚。公司有权追回本人在任职期间,因违反上述承诺给公司造成的一切经济
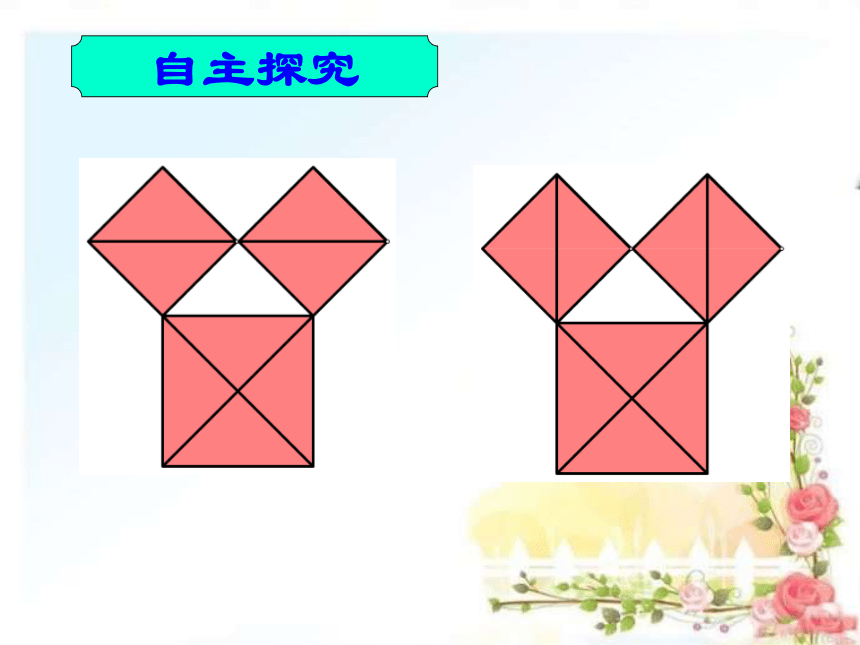
自主探究
1. 有八个全等的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗?
①
②
③
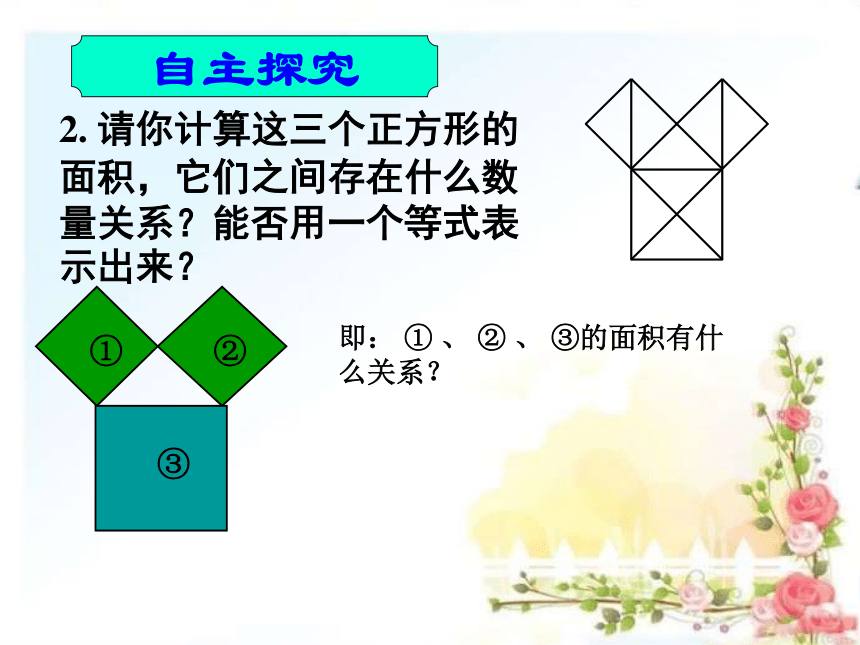
自主探究
2. 请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?
即: ① 、 ② 、 ③的面积有什么关系?
①
②
③
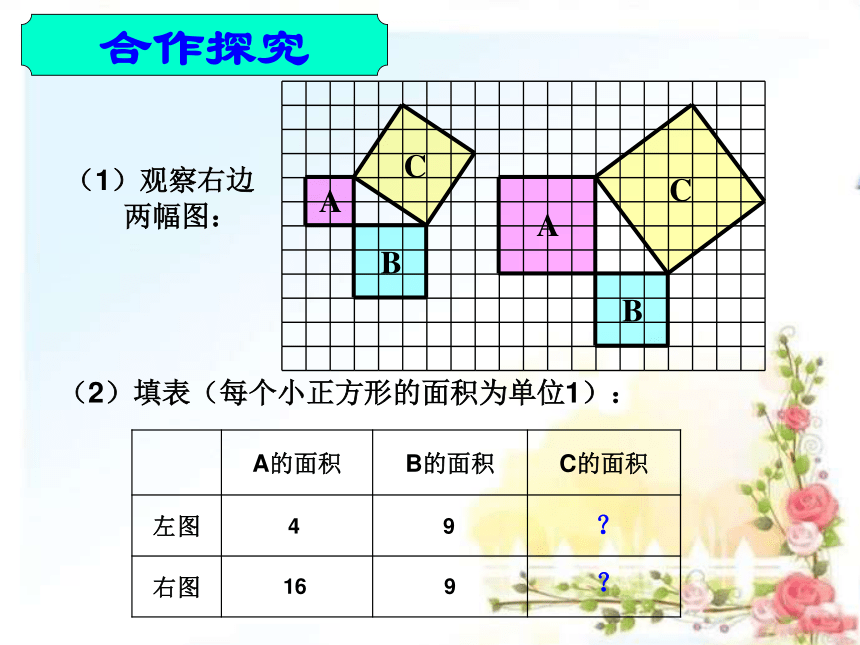
自主探究
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
?
?
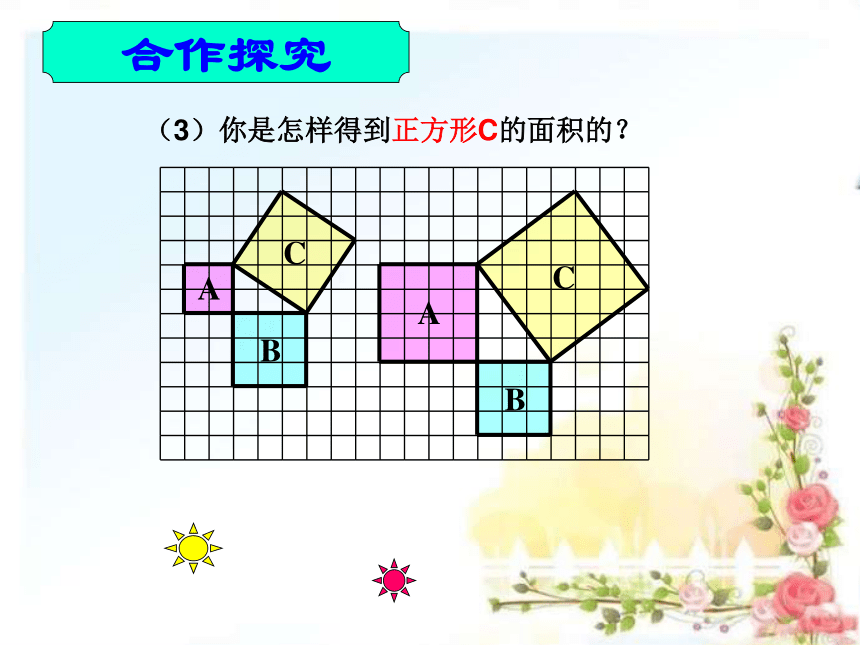
合作探究
(3)你是怎样得到正方形C的面积的?
合作探究
C
B
C
A
7
3
4
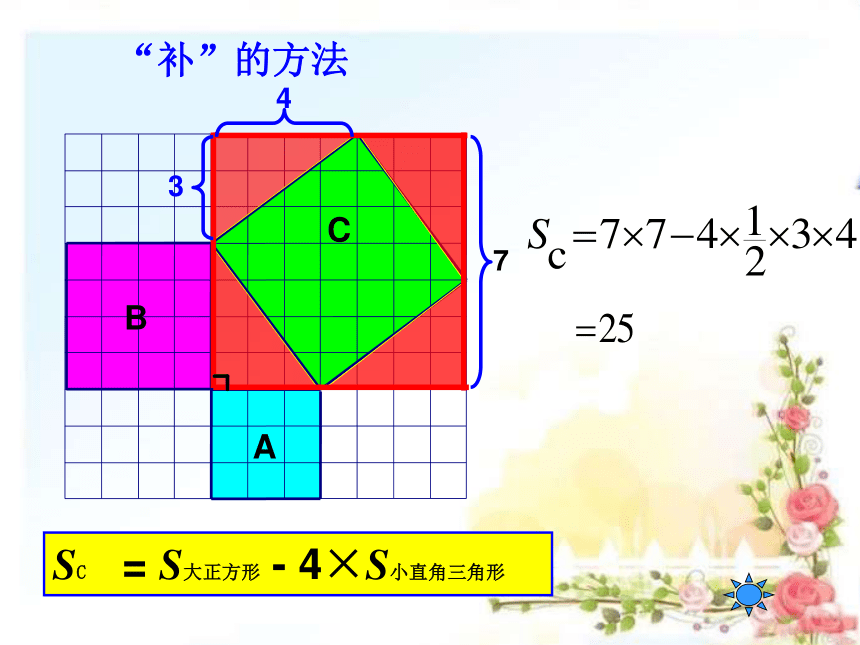
“补”的方法
SC = S大正方形 - 4×S小直角三角形
C
B
C
A
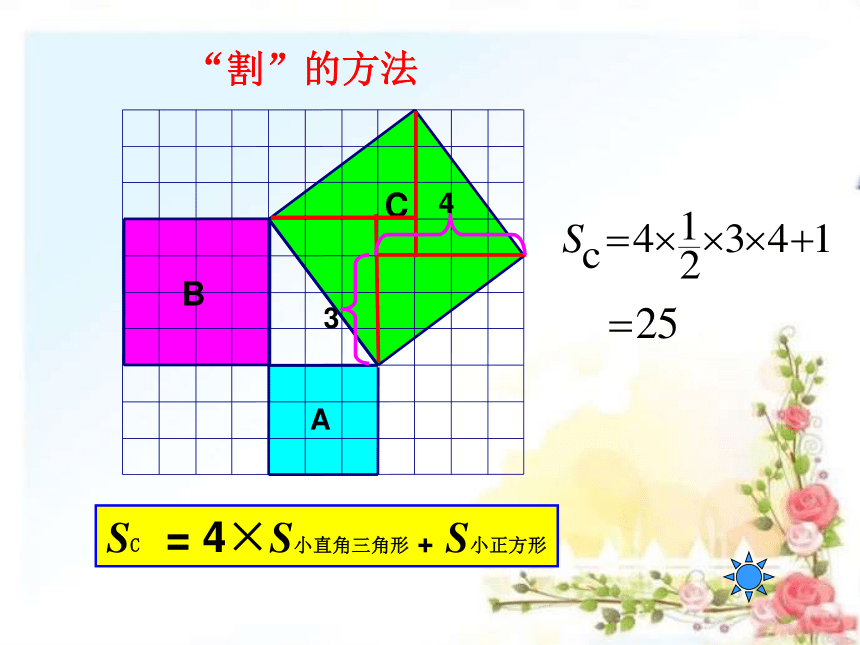
“割”的方法
3
4
SC = 4×S小直角三角形 + S小正方形
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
13
25
合作探究
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
A
B
C
C
B
A
合作探究
直角三角形的两条直角边的平方和等于斜边的平方.
命题
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
如果直角三角形两直角边分别为a、b,
斜边为c,那么
即 直角三角形两直角边的平方和
等于斜边的平方.
a
b
c
表示为:Rt△ABC中,∠C=90°,
则
定理:
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的.每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图.2002年的国际数学家大会将此图作为大会会徽.
勾股定理的由来
这个定理在中国又称为“商高定理”,商高是公元前十一世纪的中国人.当时中国的朝代是西周,是奴隶社会时期.在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话.商高说:“…故折矩,勾广三,股修四,经隅五.”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫做“商高定理”.
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
1. 已知Rt△ABC中,∠C=90°,若a=3,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
3. 一木杆在离地面3 m处折断,木杆顶端落在离木杆底端4 m处. 木杆折断之前有多高?
小试身手
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
课堂小结
1. 请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
作业
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
课外延伸
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法.
有趣的总统证法
b
c
a
b
c
a
A
B
C
D
课外延伸
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
课外延伸
第十七章 勾股定理
Zx```xk
17.1 勾股定理
第1课时
学习目标:
1)探索直角三角形两条直角边的平方和与斜边的平方的关系。
2)发展合情推理能力,体会数形结合的思想.
员工廉洁从业承诺书范文选集
领导干部的廉洁自律,是反腐败三项工作的首要任务,是搞好党风廉政建设的前提和关键。下面有小编整理的,欢迎阅读!
我作为xxxxxx公司的销售人员,为了做到廉洁从业,郑重承诺如下:
1.不以任何方式泄露、透漏公司客户、管理、产品、技术、销售等商业秘密。
2.在公司产品调价信息未执行前,不以任何明示、暗示等方式向客户或他人透漏。
3.不利用公司产品销售差价与亲属、朋友及其开办的公司发生业务,不损害公司利益。
4.不贪污、侵占公司财产,不将公款私存。
5.不以公司名义挂账、赊欠。不从客户处以任何理由借款、借物。
6.不以任何形式搞虚假报销,套取出差费。
7.不虚报、谎报、挪用业务费。
8.不接受客户的现金、物品、有价证券或高规格接待。
9.不将公司赠送客户的物品或客户赠送公司的物品占为己有。
10.不以招待客户为借口,利用公款吃喝。接待客户不
铺张浪费。
11.不介入客户与公司购销业务无关的活动。
12.不从事其他兼职工作,不推销本公司经营范围以外的产品。
如发现违反上述任何一条承诺,自愿接受公司的处罚。公司有权追回本人在任职期间,因违反上述承诺给公司造成的一切经济
自主探究
1. 有八个全等的等腰直角三角形,你能用它们拼出如图所示的三个正方形吗?
①
②
③
自主探究
2. 请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?
即: ① 、 ② 、 ③的面积有什么关系?
①
②
③
自主探究
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
?
?
合作探究
(3)你是怎样得到正方形C的面积的?
合作探究
C
B
C
A
7
3
4
“补”的方法
SC = S大正方形 - 4×S小直角三角形
C
B
C
A
“割”的方法
3
4
SC = 4×S小直角三角形 + S小正方形
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
13
25
合作探究
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
A
B
C
C
B
A
合作探究
直角三角形的两条直角边的平方和等于斜边的平方.
命题
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
如果直角三角形两直角边分别为a、b,
斜边为c,那么
即 直角三角形两直角边的平方和
等于斜边的平方.
a
b
c
表示为:Rt△ABC中,∠C=90°,
则
定理:
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的.每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图.2002年的国际数学家大会将此图作为大会会徽.
勾股定理的由来
这个定理在中国又称为“商高定理”,商高是公元前十一世纪的中国人.当时中国的朝代是西周,是奴隶社会时期.在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话.商高说:“…故折矩,勾广三,股修四,经隅五.”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.由于勾股定理的内容最早见于商高的话中,所以人们就把这个定理叫做“商高定理”.
1.成立条件: 在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
1. 已知Rt△ABC中,∠C=90°,若a=3,c=5,求b.
2. 在Rt△ABC中,∠B=90°,a=3,b=4,求c.
3. 一木杆在离地面3 m处折断,木杆顶端落在离木杆底端4 m处. 木杆折断之前有多高?
小试身手
本课我们学习了哪些知识?
用了哪些方法?
你有哪些体会?
课堂小结
1. 请你利用今天学习的面积法证明教材习题17.1第13题.
2. 课下每个同学制作一张勾股定理的数学小报,并自己上网查阅与勾股定理有关的知识,证明方法和应用等,然后小组交流、展示.
作业
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
课外延伸
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法.
有趣的总统证法
b
c
a
b
c
a
A
B
C
D
课外延伸
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
课外延伸
