2020春人教版八下数学18.1.2平行四边形的判定教学课件(2课时 26张)
文档属性
| 名称 | 2020春人教版八下数学18.1.2平行四边形的判定教学课件(2课时 26张) |  | |
| 格式 | zip | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 21:42:50 | ||
图片预览


文档简介
课件26张PPT。18.1.2 平行四边形的判定
第1课时 平行四边形的判定目习标1.掌握平行四边形的判定定理.
2.灵活运用平行四边形的判定定理.
3.灵活运用平行四边形性质和判定解决实际问题.反习馈阅读教材P45~47,完成下列问题.
1.两组对边分别 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵AB∥ ,BC∥ ,
∴四边形ABCD是平行四边形.
2.两组对边分别 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵AB= ,BC= ,
∴四边形ABCD是平行四边形.平行CDADCDDA相等3.两组对角分别 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵∠A= ,∠B= ,
∴四边形ABCD是平行四边形. 图1相等∠C∠D反习馈4.对角线 的四边形是平行四边形.
如图2,在四边形ABCD中,AC,BD相交于点O,
∵AO= ,BO= ,
∴四边形ABCD是平行四边形.
5.一组对边平行且 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵AB∥ ,AB= ,
∴四边形ABCD是平行四边形.互相平分CODOCDCD
图2
图1相等讲校坛例1 (教材P46例3)如图,?ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 【思路点拨】 根据平行四边形的性质可以得出OA=OC,OB=OD,再结合AE=CF,得出四边形BFDE的对角线互相平分,即可得出四边形BFDE是平行四边形.【解答】 证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO.
又∵AE=CF,
∴EO=FO.
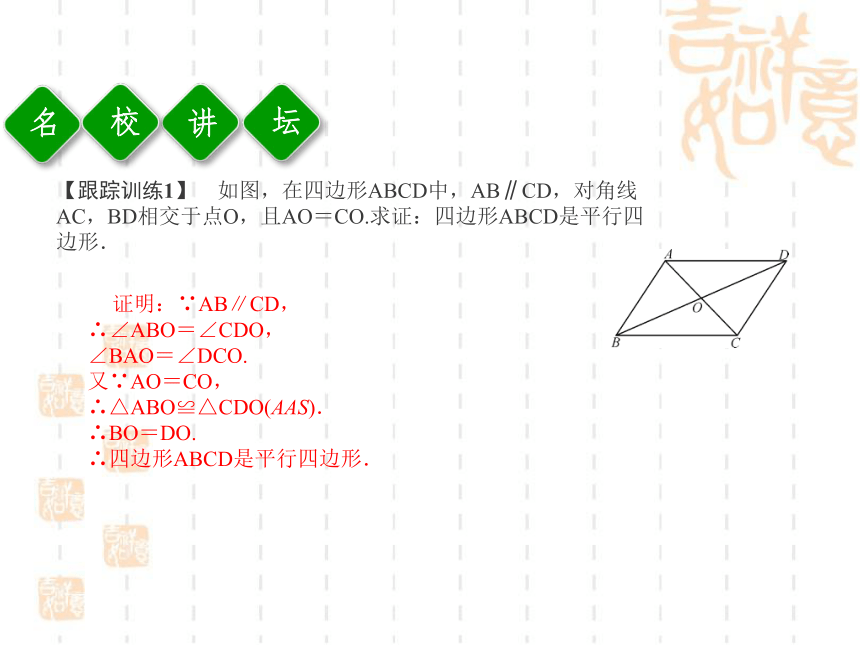
∴四边形BFDE是平行四边形.讲校坛【跟踪训练1】 如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,且AO=CO.求证:四边形ABCD是平行四边形.证明:∵AB∥CD,
∴∠ABO=∠CDO,
∠BAO=∠DCO.
又∵AO=CO,
∴△ABO≌△CDO(AAS).
∴BO=DO.
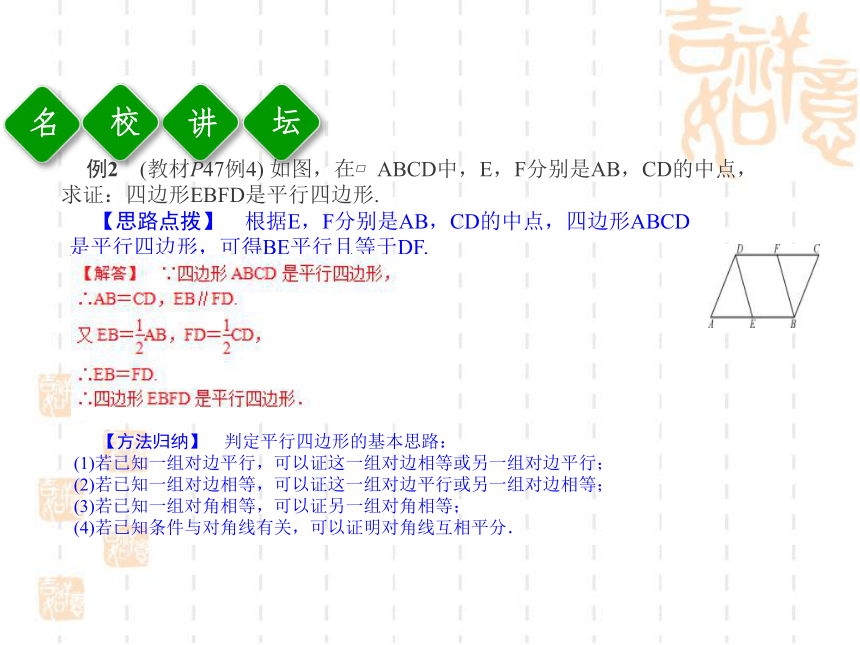
∴四边形ABCD是平行四边形.讲校坛例2 (教材P47例4) 如图,在?ABCD中,E,F分别是AB,CD的中点,求证:四边形EBFD是平行四边形. 【思路点拨】 根据E,F分别是AB,CD的中点,四边形ABCD是平行四边形,可得BE平行且等于DF.【方法归纳】 判定平行四边形的基本思路:
(1)若已知一组对边平行,可以证这一组对边相等或另一组对边平行;
(2)若已知一组对边相等,可以证这一组对边平行或另一组对边相等;
(3)若已知一组对角相等,可以证另一组对角相等;
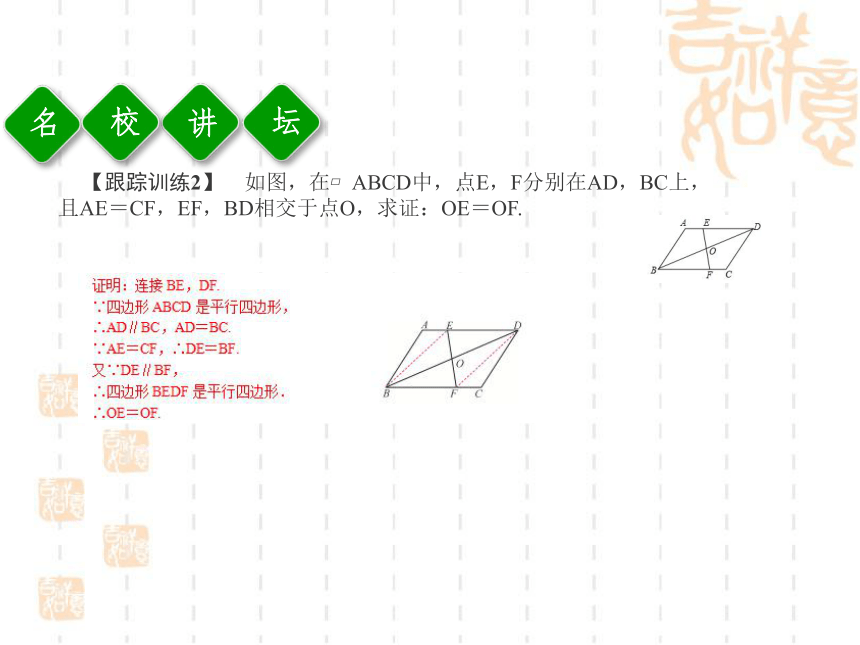
(4)若已知条件与对角线有关,可以证明对角线互相平分.讲校坛【跟踪训练2】 如图,在?ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF. 训固练1.如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )A.AB=DC B.∠1=∠2
C.AB=AD D.AD=BCD2.下面给出的是四边形ABCD中∠A,∠B,∠C,∠D的度数比,其中能判断出四边形是平行四边形的是( )
A.4∶3∶2∶1 B.3∶2∶3∶2
C.3∶3∶2∶2 D.3∶2∶2∶1B3.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 (只添一个即可),使四边形ABCD是平行四边形.BO=DO(答案不唯一)训固练训固练5.如图,在四边形ABCD中,AB∥CD,点E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.小堂结1.平行四边形判定定理:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形.
2.平行四边形性质和判定的运用.第2课时 三角形的中位线目习标1.理解三角形中位线的概念,掌握它的性质.
2.能较熟练地应用三角形中位线性质进行有关的证明和计算.反习馈阅读教材P47~49,完成下列问题.
1.三角形的中位线的定义:连接三角形两边 的线段叫做三角形的中位线.
2.三角形的中位线定理:三角形的中位线 于三角形的第三边,并且等于第三边的 .中点平行一半如图,∵DE是△ABC的中位线,
∴DE∥ ,且DE= .
3.一个三角形有 中位线.BCBC三条讲校坛例1 (教材P48探究)如图,D,E分别为△ABC边AB,AC的中点.求证:DE∥BC,且DE= BC.【思路点拨】 本题既要证明两条线段所在的直线平行,又要证明其中一条线段的长等于另一条线段长的一半.将DE延长一倍后,可以将证明DE= BC转化为证明延长后的线段与BC相等.又由于E是AC的中点,根据对角线互相平分的四边形是平行四边形构造一个平行四边形,利用平行四边形的性质进行证明.讲校坛讲校坛【跟踪训练1】 如图,在?ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5 cm,则AD的长为 cm.10讲校坛例2 (教材P49练习T1)如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?【解答】 能画出三个平行四边形,根据一组对边平行且相等的四边形是平行四边形可得四边形BEFD、四边形DECF、四边形ADEF为平行四边形.讲校坛【跟踪训练2】 如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求证:四边形DECF是平行四边形.证明:∵D,E,F分别为AB,BC,CA的中点,
∴DF,DE为△ABC的中位线.
∴DF∥BC,DE∥AC.
∴四边形DECF是平行四边形.训固练1.如图,在等边△ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
A.150° B.120° C.60° D.30°2.如图,△ABC中,D,E,F,G分别是AB,AC,AD,AE的中点,若BC=8,则DE+FG=( )
A.4.5 B.6 C.7 D.8BB训固练3.已知△ABC的各边长度分别为3 cm,4 cm,5 cm,则连接各边中点的三角形周长为( )
A.2 cm B.7 cm C.5 cm D.6 cm
4.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,CF=1,DF交CE于点G,且EG=CG,则BC= .D2训固练训固练6.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°.求∠PFE的度数.小堂结1.三角形的中位线定理.
2.三角形的中位线定理不仅给出了中位线与第三边的位置关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.THANK YOU!
第1课时 平行四边形的判定目习标1.掌握平行四边形的判定定理.
2.灵活运用平行四边形的判定定理.
3.灵活运用平行四边形性质和判定解决实际问题.反习馈阅读教材P45~47,完成下列问题.
1.两组对边分别 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵AB∥ ,BC∥ ,
∴四边形ABCD是平行四边形.
2.两组对边分别 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵AB= ,BC= ,
∴四边形ABCD是平行四边形.平行CDADCDDA相等3.两组对角分别 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵∠A= ,∠B= ,
∴四边形ABCD是平行四边形. 图1相等∠C∠D反习馈4.对角线 的四边形是平行四边形.
如图2,在四边形ABCD中,AC,BD相交于点O,
∵AO= ,BO= ,
∴四边形ABCD是平行四边形.
5.一组对边平行且 的四边形是平行四边形.
如图1,在四边形ABCD中,
∵AB∥ ,AB= ,
∴四边形ABCD是平行四边形.互相平分CODOCDCD
图2
图1相等讲校坛例1 (教材P46例3)如图,?ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 【思路点拨】 根据平行四边形的性质可以得出OA=OC,OB=OD,再结合AE=CF,得出四边形BFDE的对角线互相平分,即可得出四边形BFDE是平行四边形.【解答】 证明:∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO.
又∵AE=CF,
∴EO=FO.
∴四边形BFDE是平行四边形.讲校坛【跟踪训练1】 如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,且AO=CO.求证:四边形ABCD是平行四边形.证明:∵AB∥CD,
∴∠ABO=∠CDO,
∠BAO=∠DCO.
又∵AO=CO,
∴△ABO≌△CDO(AAS).
∴BO=DO.
∴四边形ABCD是平行四边形.讲校坛例2 (教材P47例4) 如图,在?ABCD中,E,F分别是AB,CD的中点,求证:四边形EBFD是平行四边形. 【思路点拨】 根据E,F分别是AB,CD的中点,四边形ABCD是平行四边形,可得BE平行且等于DF.【方法归纳】 判定平行四边形的基本思路:
(1)若已知一组对边平行,可以证这一组对边相等或另一组对边平行;
(2)若已知一组对边相等,可以证这一组对边平行或另一组对边相等;
(3)若已知一组对角相等,可以证另一组对角相等;
(4)若已知条件与对角线有关,可以证明对角线互相平分.讲校坛【跟踪训练2】 如图,在?ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF. 训固练1.如图所示,AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )A.AB=DC B.∠1=∠2
C.AB=AD D.AD=BCD2.下面给出的是四边形ABCD中∠A,∠B,∠C,∠D的度数比,其中能判断出四边形是平行四边形的是( )
A.4∶3∶2∶1 B.3∶2∶3∶2
C.3∶3∶2∶2 D.3∶2∶2∶1B3.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 (只添一个即可),使四边形ABCD是平行四边形.BO=DO(答案不唯一)训固练训固练5.如图,在四边形ABCD中,AB∥CD,点E,F为对角线AC上两点,且AF=CE,DF∥BE.求证:四边形ABCD为平行四边形.小堂结1.平行四边形判定定理:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形.
2.平行四边形性质和判定的运用.第2课时 三角形的中位线目习标1.理解三角形中位线的概念,掌握它的性质.
2.能较熟练地应用三角形中位线性质进行有关的证明和计算.反习馈阅读教材P47~49,完成下列问题.
1.三角形的中位线的定义:连接三角形两边 的线段叫做三角形的中位线.
2.三角形的中位线定理:三角形的中位线 于三角形的第三边,并且等于第三边的 .中点平行一半如图,∵DE是△ABC的中位线,
∴DE∥ ,且DE= .
3.一个三角形有 中位线.BCBC三条讲校坛例1 (教材P48探究)如图,D,E分别为△ABC边AB,AC的中点.求证:DE∥BC,且DE= BC.【思路点拨】 本题既要证明两条线段所在的直线平行,又要证明其中一条线段的长等于另一条线段长的一半.将DE延长一倍后,可以将证明DE= BC转化为证明延长后的线段与BC相等.又由于E是AC的中点,根据对角线互相平分的四边形是平行四边形构造一个平行四边形,利用平行四边形的性质进行证明.讲校坛讲校坛【跟踪训练1】 如图,在?ABCD中,对角线AC,BD相交于点O,点E是AB的中点,OE=5 cm,则AD的长为 cm.10讲校坛例2 (教材P49练习T1)如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?【解答】 能画出三个平行四边形,根据一组对边平行且相等的四边形是平行四边形可得四边形BEFD、四边形DECF、四边形ADEF为平行四边形.讲校坛【跟踪训练2】 如图,在△ABC中,D,E,F分别为边AB,BC,CA的中点.求证:四边形DECF是平行四边形.证明:∵D,E,F分别为AB,BC,CA的中点,
∴DF,DE为△ABC的中位线.
∴DF∥BC,DE∥AC.
∴四边形DECF是平行四边形.训固练1.如图,在等边△ABC中,点D,E分别为AB,AC的中点,则∠DEC的度数为( )
A.150° B.120° C.60° D.30°2.如图,△ABC中,D,E,F,G分别是AB,AC,AD,AE的中点,若BC=8,则DE+FG=( )
A.4.5 B.6 C.7 D.8BB训固练3.已知△ABC的各边长度分别为3 cm,4 cm,5 cm,则连接各边中点的三角形周长为( )
A.2 cm B.7 cm C.5 cm D.6 cm
4.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上一点,CF=1,DF交CE于点G,且EG=CG,则BC= .D2训固练训固练6.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°.求∠PFE的度数.小堂结1.三角形的中位线定理.
2.三角形的中位线定理不仅给出了中位线与第三边的位置关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.THANK YOU!
