湘教版数学九年级下册第2章 圆 单元测试卷(含答案)
文档属性
| 名称 | 湘教版数学九年级下册第2章 圆 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 21:03:46 | ||
图片预览

文档简介
湘教版数学九年级下册第2章 圆 单元测试卷
[时间:90分钟 分值:120分] 第Ⅰ卷(选择题 共30分)
一、选择题(每小题3分,共30分)
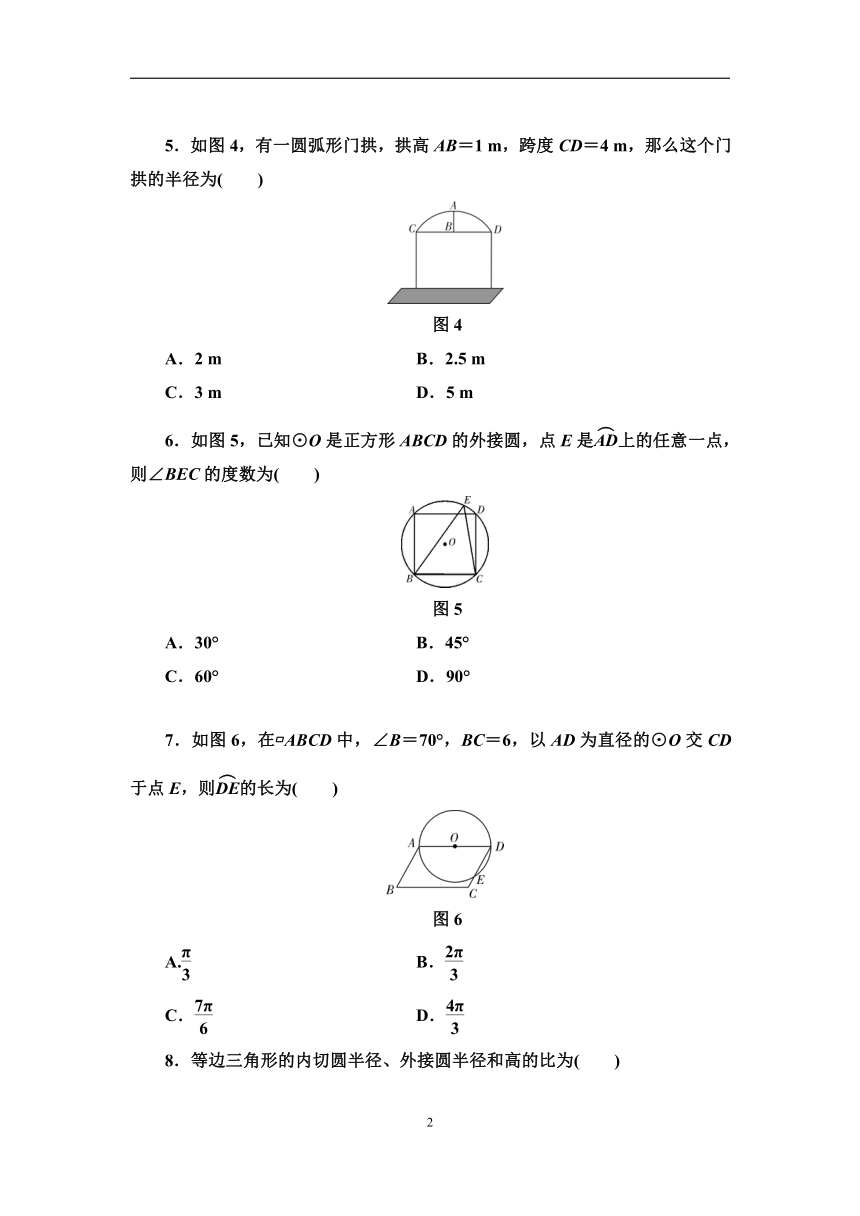
1.下列说法错误的是( )
A.圆上的点到圆心的距离相等 B.过圆心的线段是直径
C.直径是圆中最长的弦 D.半径相等的2个圆是等圆
2.如图1,C,D是以线段AB为直径的⊙O上的两点,若CA=CD,且∠ACD=40°,则∠CAB等于( )
图1
A.10° B.20°
C.30° D.40°
3.如图2,在△ABC中,已知AB=AC=4 cm,BC=6 cm,D是BC的中点,以点D为圆心作一个半径为3 cm的圆,则下列说法正确的是( )
图2
A.点A在⊙D外 B.点B在⊙D内
C.点C在⊙D上 D.无法确定
4.如图3,四边形ABCD的边AB,BC,CD,DA和⊙O分别相切于点L,M,N,P.若四边形ABCD的周长为20,则AB+CD等于( )
图3
A.5 B.8
C.10 D.12
5.如图4,有一圆弧形门拱,拱高AB=1 m,跨度CD=4 m,那么这个门拱的半径为( )
图4
A.2 m B.2.5 m
C.3 m D.5 m
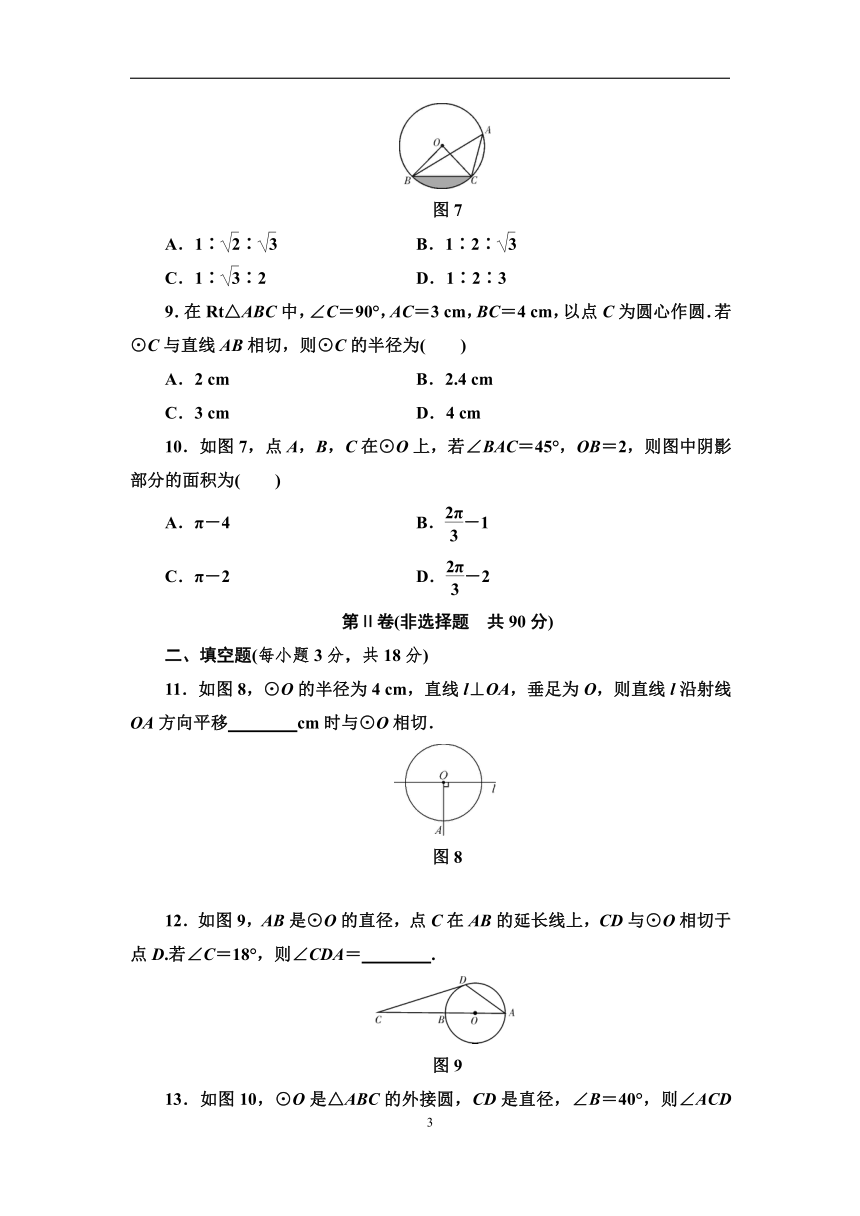
6.如图5,已知⊙O是正方形ABCD的外接圆,点E是上的任意一点,则∠BEC的度数为( )
图5
A.30° B.45°
C.60° D.90°
7.如图6,在?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为( )
图6
A. B.
C. D.
8.等边三角形的内切圆半径、外接圆半径和高的比为( )
图7
A.1∶∶ B.1∶2∶
C.1∶∶2 D.1∶2∶3
9.在Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,以点C为圆心作圆.若⊙C与直线AB相切,则⊙C的半径为( )
A.2 cm B.2.4 cm
C.3 cm D.4 cm
10.如图7,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π-4 B.-1
C.π-2 D.-2
第Ⅱ卷(非选择题 共90分)
二、填空题(每小题3分,共18分)
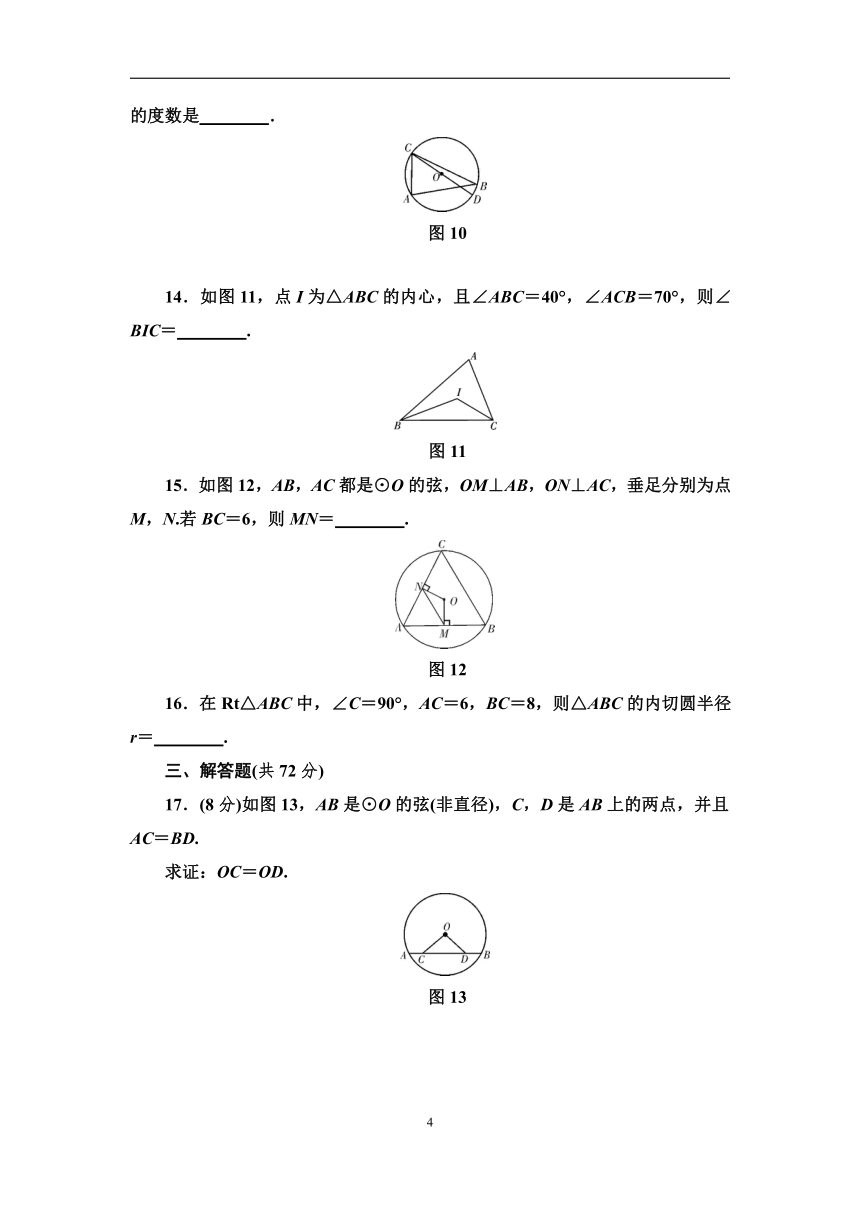
11.如图8,⊙O的半径为4 cm,直线l⊥OA,垂足为O,则直线l沿射线OA方向平移 cm时与⊙O相切.
图8
12.如图9,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D.若∠C=18°,则∠CDA= .
图9
13.如图10,⊙O是△ABC的外接圆,CD是直径,∠B=40°,则∠ACD的度数是 .
图10
14.如图11,点I为△ABC的内心,且∠ABC=40°,∠ACB=70°,则∠BIC= .
图11
15.如图12,AB,AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为点M,N.若BC=6,则MN= .
图12
16.在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径r= .
三、解答题(共72分)
17.(8分)如图13,AB是⊙O的弦(非直径),C,D是AB上的两点,并且AC=BD.
求证:OC=OD.
图13
18.(8分)如图14,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO,交⊙O于点D.
图14
(1)求∠BAD的度数;
(2)求证:△ABC为等边三角形.
19.(10分)如图15,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5 cm,弦DE=8 cm,求直尺的宽.
图15
20.(11分)如图16,AB是⊙O的直径,AC与⊙O相切,切点为A,D为⊙O上一点,AD与OC相交于点E,且∠DAB=∠C.求证:OC∥BD.
图16
21.(11分)如图17,已知点E在△ABC的边AB上,∠C=90°,以AE为直径的⊙O切BC于点D.
(1)求证:AD平分∠BAC;
(2)已知∠B=30°,AD=2,求图中阴影部分的面积.
图17
22.(12分)如图18,点D是以AB为直径的⊙O上一点,过点B作⊙O的切线,交AD的延长线于点C,E是BC的中点,连接DE并延长,与AB的延长线交于点F.
(1)求证:DF是⊙O的切线;
(2)若OB=BF,EF=4,求AD的长.
图18
23.(12分)[2018·鄂州]如图19,四边形ABCD内接于⊙O,BC为⊙O的直径,AC与BD交于点E,P为CB延长线上一点,连接PA,且∠PAB=∠ADB.
(1)求证:PA为⊙O的切线;
(2)若AB=6,tan∠ADB=,求PB的长;
(3)在(2)的条件下,若AD=CD,求△CDE的面积.
图19
参考答案
第2章质量评估试卷
1.B 2.B 3.C 4.C 5.B 6.B 7.B
8.D 9.B 10.C
11.4 12.126° 13.50° 14.125° 15.3
16.2 17.略 18.(1)90° (2)略
19.3 cm 20.略
21.(1)略 (2)2-
22.(1)略 (2)6 23.(1)略 (2) (3)5
8
