湘教版数学九年级下册第3章 投影与视图 单元测试卷(含答案)
文档属性
| 名称 | 湘教版数学九年级下册第3章 投影与视图 单元测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 21:07:54 | ||
图片预览


文档简介
湘教版数学九年级下册第3章 投影与视图 单元测试卷[时间:90分钟 分值:120分] 第Ⅰ卷(选择题 共30分)
一、选择题(每小题3分,共30分)
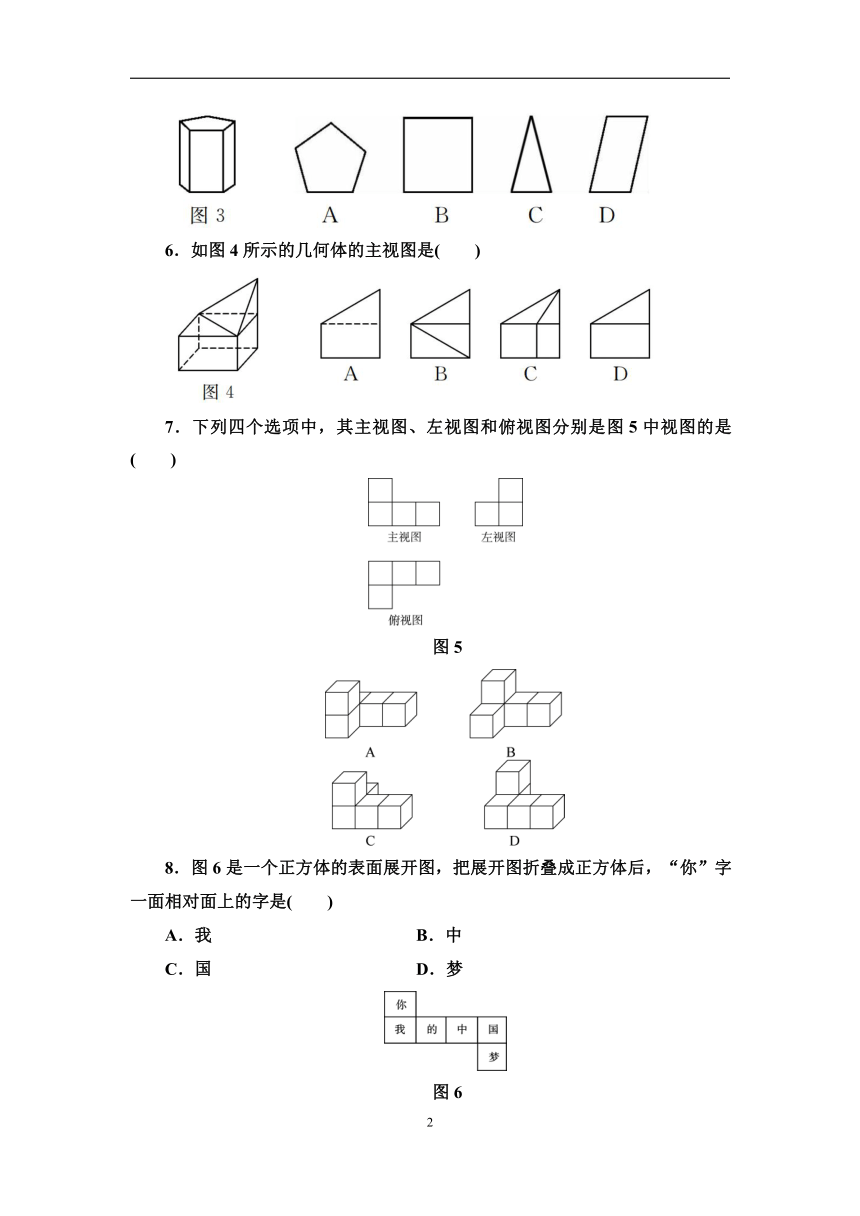
1.下面的几何体中,主视图为圆的是( )
2.如图1,该几何体的俯视图是( )
3.[2019·成都]如图2所示的几何体是由6个大小相同的小立方块搭成的,它的左视图是( )
4.一根笔直小木棒(记为线段AB)的正投影为线段CD,则下列各式中,一定成立的是( )
A.AB=CD B.AB≤CD
C.AB>CD D.AB≥CD
5.把一个正五棱柱按如图3所示的方式摆放,则投射线由正前方射到后方时所形成的影子是( )
6.如图4所示的几何体的主视图是( )
7.下列四个选项中,其主视图、左视图和俯视图分别是图5中视图的是( )
图5
8.图6是一个正方体的表面展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是( )
A.我 B.中
C.国 D.梦
图6
9.已知圆锥的底面半径为4 cm,母线长为6 cm,则它的侧面展开图的面积等于( )
图7
A.24 cm2 B.48 cm2
C.24π cm2 D.48π cm2
10.如图7,用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10 cm,那么这张扇形纸板的面积是( )
A.240π cm2 B.480π cm2
C.1 200π cm2 D.2 400π cm2
第Ⅱ卷(非选择题 共90分)
二、填空题(每小题3分,共18分)
11.两个物体映在地上的影子有时在同侧,有时在异侧,则这是 投影(填“平行”或“中心”).
12.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是 (结果保留π).
13.一个几何体的三视图如图8所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是 .
图8
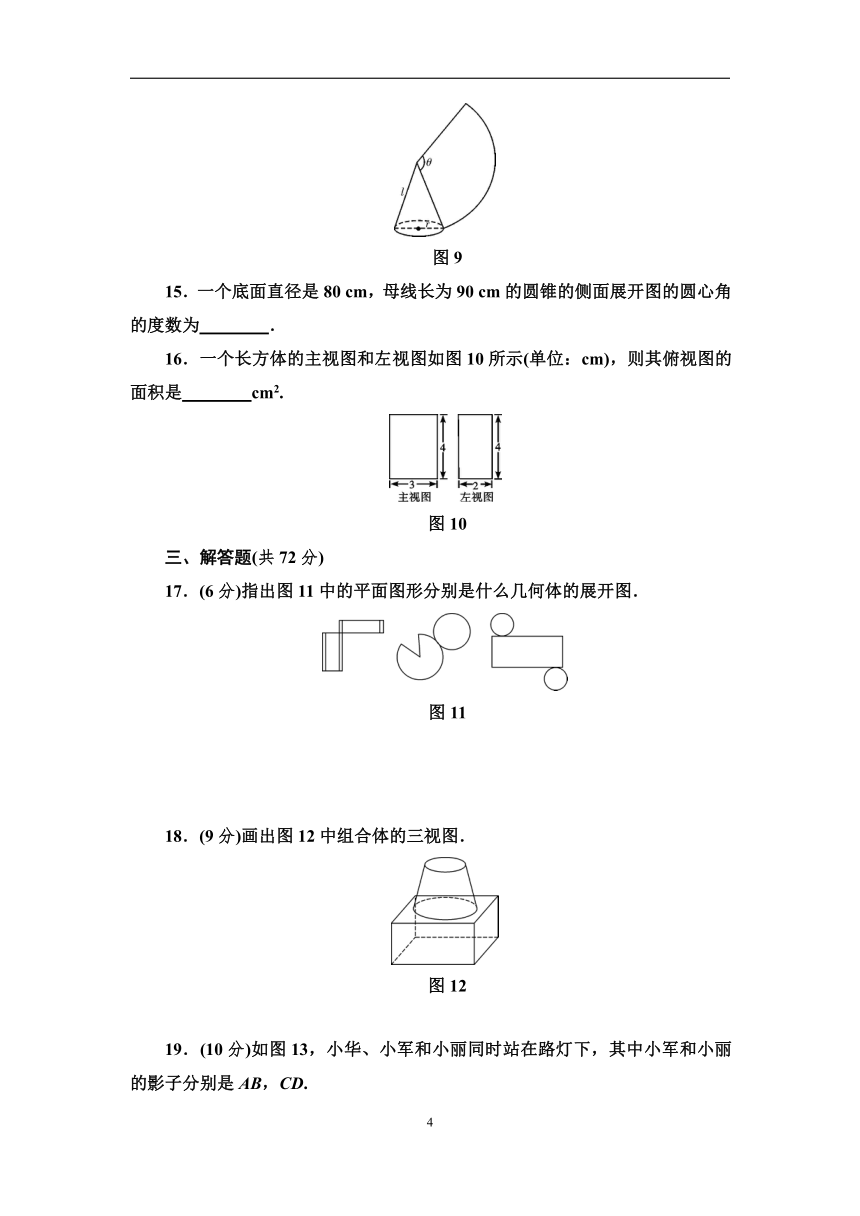
14.如图9,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥的母线长l为 .
图9
15.一个底面直径是80 cm,母线长为90 cm的圆锥的侧面展开图的圆心角的度数为 .
16.一个长方体的主视图和左视图如图10所示(单位:cm),则其俯视图的面积是 cm2.
图10
三、解答题(共72分)
17.(6分)指出图11中的平面图形分别是什么几何体的展开图.
图11
18.(9分)画出图12中组合体的三视图.
图12
19.(10分)如图13,小华、小军和小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示).
图13
20.(11分)如图14,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高.
图14
21.(12分)图15是由一些棱长都为1 cm的小正方体组合成的简单几何体.
图15
图16
(1)该几何体的主视图已画出,请在图16中画出它的左视图和俯视图;
(2)如果在这个几何体上再添加一些同样大小的小正方体,并保持俯视图和左视图不变,最多可以再添加 个小正方体.
22.(12分)小亮要利用废纸板做一个三棱柱形状的无盖的笔筒,设计三棱柱的立体模型如图17所示.
图17
(1)请画出该立体模型的三视图;
(2)该笔筒至少要用多少废纸板?
23.(12分)某冷饮厂要加工一批冰激凌蛋筒,设计师给出了封闭蛋筒的三视图(如图18所示).请你按照三视图,确定制作每个蛋筒所需的包装材料的面积(π取3.14,不计损耗).
图18
参考答案
第3章质量评估试卷
1.C 2.C 3.B 4.D 5.B 6.D 7.A
8.D 9.C 10.A
11.中心 12.20π 13.abc
14.6 15.160°
16.6 17.长方体;圆锥;圆柱.
18.如图:
19.(1)如图,点P就是所求的点
(2)如图,EF就是小华此时在路灯下的影子
20.4 cm
21.(1)如图:
(2)6
22.(1)如图:
(2)360 cm2
23.制作每个蛋筒所需的包装材料的面积约为282.6 cm2
8
