湘教版数学九年级下册期末数学模拟试卷(含答案)
文档属性
| 名称 | 湘教版数学九年级下册期末数学模拟试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 151.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 20:41:53 | ||
图片预览

文档简介
湘教版数学九年级下册期末模拟试卷
[时间:90分钟 分值:120分]
第Ⅰ卷(选择题 共30分)
一、选择题(每小题3分,共30分)
1.如图1是一个底面为正方形的长方体,下面有关它的三视图的说法正确的是( )
图1
A.俯视图与主视图相同 B.左视图与主视图相同
C.左视图与俯视图相同 D.三个视图都相同
2.已知等腰三角形的腰长为6 cm,底边长为4 cm,以这个等腰三角形的顶角的顶点为圆心、5 cm为半径画圆,那么该圆与等腰三角形的底边的位置关系是( )
A.相离 B.相切
C.相交 D.不能确定
3.对于抛物线y=-(x+1)2+3,有下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小.其中正确结论的个数为( )
A.1 B.2
C.3 D.4
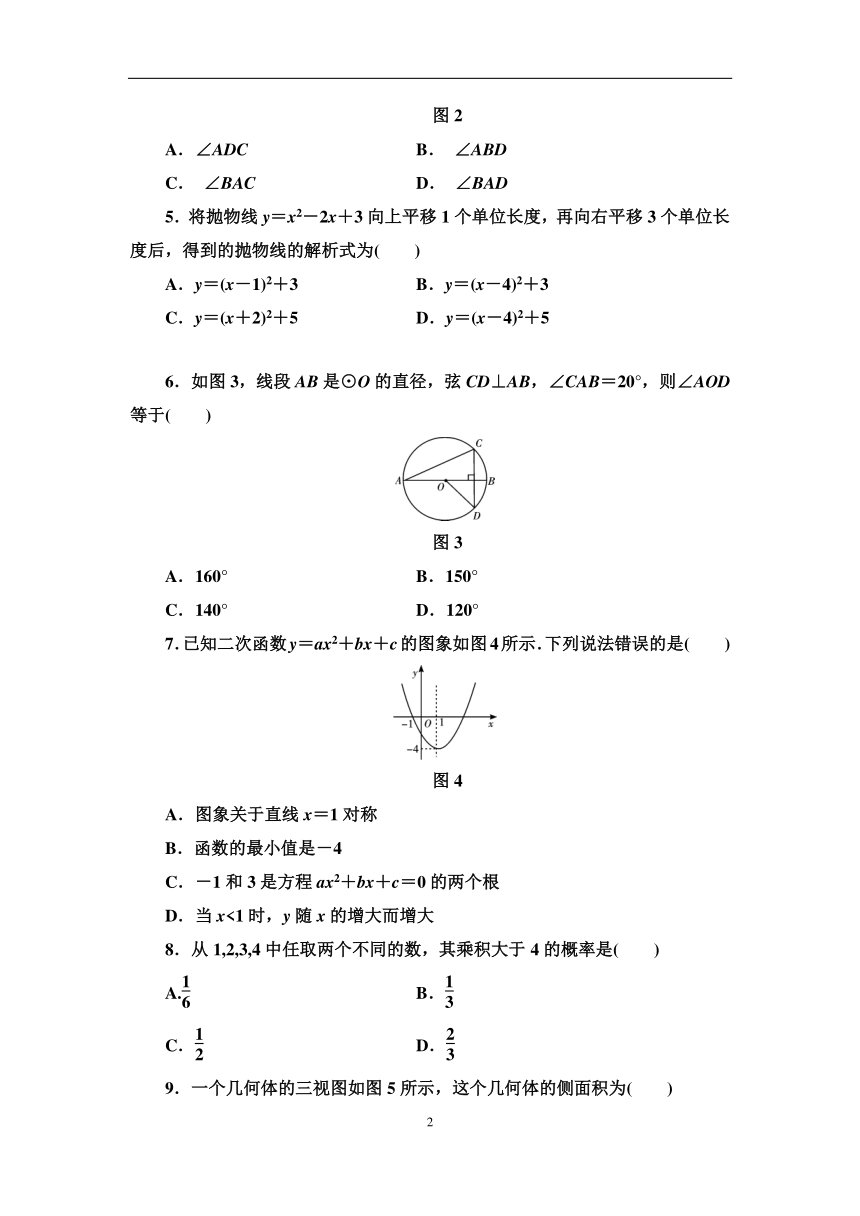
4.如图2,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的角是( )
图2
A.∠ADC B. ∠ABD
C. ∠BAC D. ∠BAD
5.将抛物线y=x2-2x+3向上平移1个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )
A.y=(x-1)2+3 B.y=(x-4)2+3
C.y=(x+2)2+5 D.y=(x-4)2+5
6.如图3,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=20°,则∠AOD等于( )
图3
A.160° B.150°
C.140° D.120°
7.已知二次函数y=ax2+bx+c的图象如图4所示.下列说法错误的是( )
图4
A.图象关于直线x=1对称
B.函数的最小值是-4
C.-1和3是方程ax2+bx+c=0的两个根
D.当x<1时,y随x的增大而增大
8.从1,2,3,4中任取两个不同的数,其乘积大于4的概率是( )
A. B.
C. D.
9.一个几何体的三视图如图5所示,这个几何体的侧面积为( )
A.2π cm2 B.4π cm2
C.8π cm2 D.16π cm2
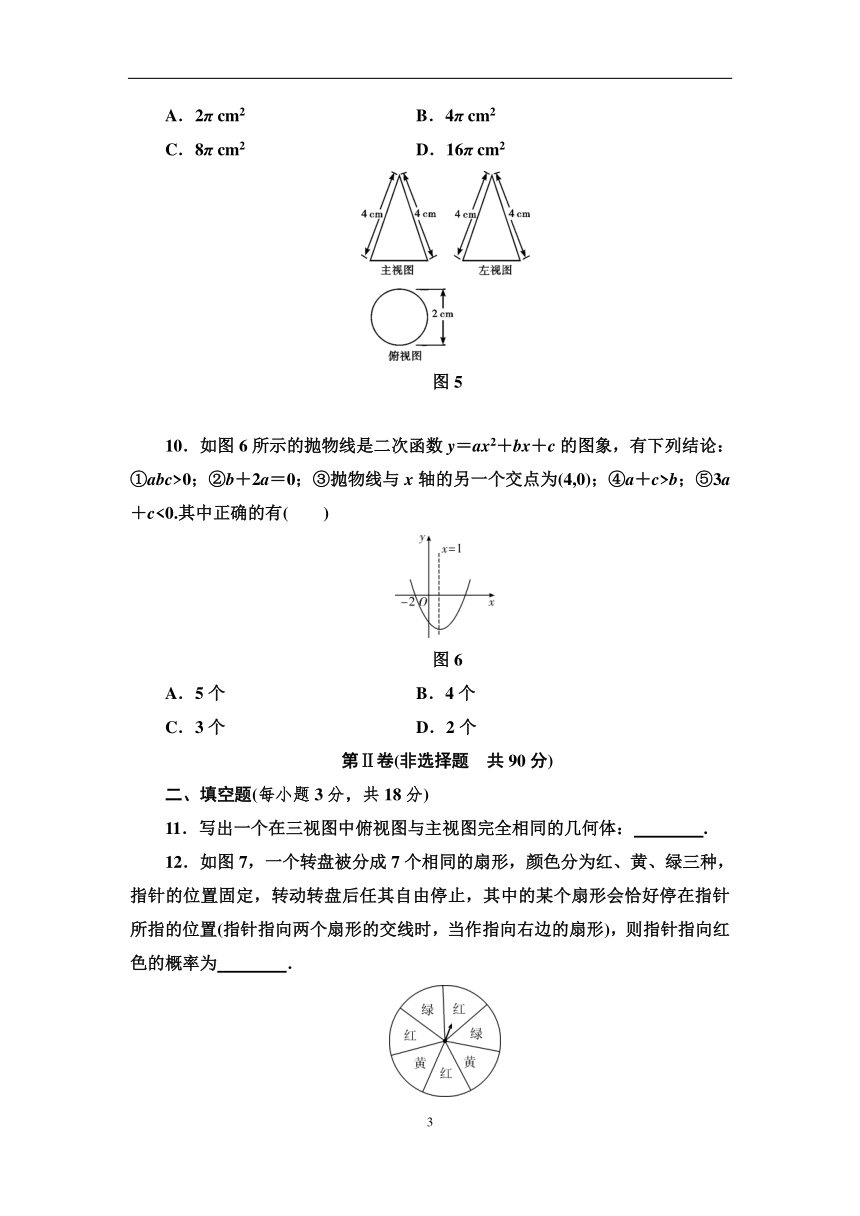
图5
10.如图6所示的抛物线是二次函数y=ax2+bx+c的图象,有下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的有( )
图6
A.5个 B.4个
C.3个 D.2个
第Ⅱ卷(非选择题 共90分)
二、填空题(每小题3分,共18分)
11.写出一个在三视图中俯视图与主视图完全相同的几何体: .
12.如图7,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为 .
图7
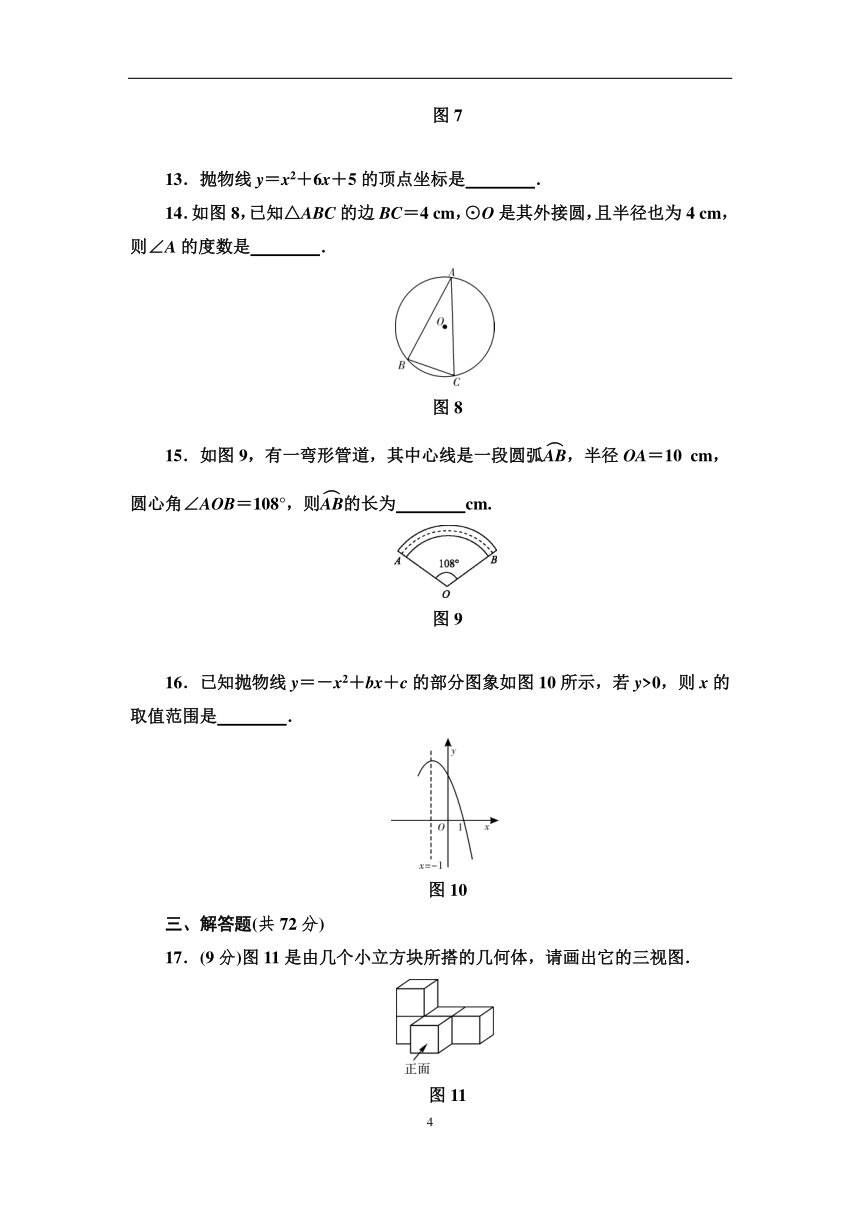
13.抛物线y=x2+6x+5的顶点坐标是 .
14.如图8,已知△ABC的边BC=4 cm,⊙O是其外接圆,且半径也为4 cm,则∠A的度数是 .
图8
15.如图9,有一弯形管道,其中心线是一段圆弧,半径OA=10 cm,圆心角∠AOB=108°,则的长为 cm.
图9
16.已知抛物线y=-x2+bx+c的部分图象如图10所示,若y>0,则x的取值范围是 .
图10
三、解答题(共72分)
17.(9分)图11是由几个小立方块所搭的几何体,请画出它的三视图.
图11
18.(9分)如图12,A,B是⊙O上的两点,∠AOB=120°,点C是的中点,试判断四边形OACB的形状,并说明理由.
图12
19.(9分)如图13,已知二次函数y=-x2+bx+c的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
图13
20.(10分)一个不透明的布袋里装有2个白球、1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为.
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表法或树状图法求出两次都摸到红球的概率.
21.(11分)某超市销售一种商品,成本为每千克40元,规定每千克售价不低于成本,且不高于80元.经市场调查,发现每天的销售量y(kg)与每千克售价x(元) 满足一次函数关系,部分数据如下表:
售价x/(元/kg) 50 60 70
销售量y/kg 100 80 60
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式;
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
22.(12分)如图14,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到点O,使AO=AC,以点O为圆心,OA的长为半径作⊙O,交BA的延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
图14
23.(12分)如图15,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(-3,0)两点,与y轴交于点C,且OB=OC.
(1)求抛物线的解析式;
(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;
(3)已知抛物线上的两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线,交MN于点E.
①求DE的最大值;
②点D关于点E的对称点为F,当m为何值时,四边形MDNF为矩形?
图15
参考答案
期末质量评估试卷
1.B 2.A 3.C 4.D 5.B 6.C 7.D
8.C 9.B 10.B
11.球(答案不唯一) 12. 13.(-3,-4)
14.30° 15.6π
16.-3
18.四边形OACB是菱形.理由略
19.(1)y=-x2+4x-6 (2)6
20.(1)红球有2个 (2),图略
21.(1)y=-2x+200(40≤x≤80)
(2)W=-2x2+280x-8 000(40≤x≤80)
(3)当40≤x<70时,W随x的增大而增大;当70
23.(1)y=-(x+1)(x+3)=-x2-4x-3
(2)点P的坐标为,,(-2,1)或
(3)①DE的最大值为4 ②m的值为-4-或-4+时,四边形MDNF为矩形
2
同课章节目录
