2019-2020学年华东师大版数学九年级下册 第27章 圆 单元综合卷(解析版)
文档属性
| 名称 | 2019-2020学年华东师大版数学九年级下册 第27章 圆 单元综合卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1013.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 20:58:31 | ||
图片预览



文档简介
第27章 检测试题
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.☉O的直径为10,点P到圆心O的距离为3,点P与☉O的位置关系是( )
(A)无法确定 (B)点P在☉O外
(C)点P在☉O上 (D)点P在☉O内
2.如图,在☉O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
第2题图
(A)AD=2OB (B)CE=EO
(C)∠OCE=40° (D)∠BOC=2∠BAD
3.圆锥的母线长为10,侧面积为60π,则这个圆锥的底面周长为( )
(A)10π (B)12π (C)16π (D)20π
4.如图,△ABC的边AC与☉O相交于C,D两点,且经过圆心O,边AB与☉O相切,切点为B.已知∠A=30°,则∠C的大小是( )
第4题图
(A)30° (B)45° (C)60° (D)40°
5.如图,四边形ABCD内接于☉O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
第5题图
(A)100° (B)112.5° (C)120° (D)135°
6.如图,☉O的半径为1,△ABC是☉O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
第6题图
(A)2 (B) (C) (D)
7.正六边形的边心距为,则该正六边形的边长是( )
(A) (B)2 (C)3 (D)2
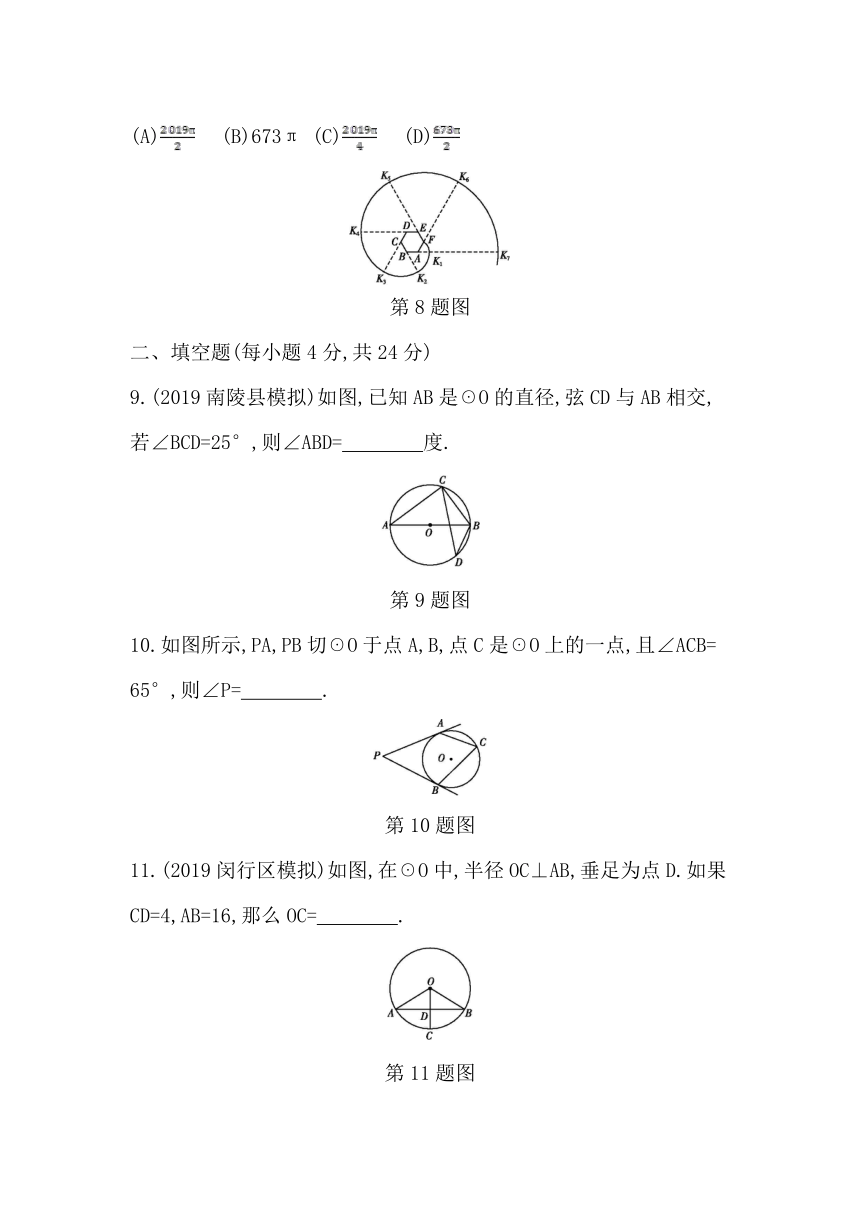
8.如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,
l6,….当AB=1时,l2 019等于( )
(A) (B)673π (C) (D)
第8题图
二、填空题(每小题4分,共24分)
9.(2019南陵县模拟)如图,已知AB是☉O的直径,弦CD与AB相交,若∠BCD=25°,则∠ABD= 度.?
第9题图
10.如图所示,PA,PB切☉O于点A,B,点C是☉O上的一点,且∠ACB=
65°,则∠P= .?
第10题图
11.(2019闵行区模拟)如图,在☉O中,半径OC⊥AB,垂足为点D.如果CD=4,AB=16,那么OC= .?
第11题图
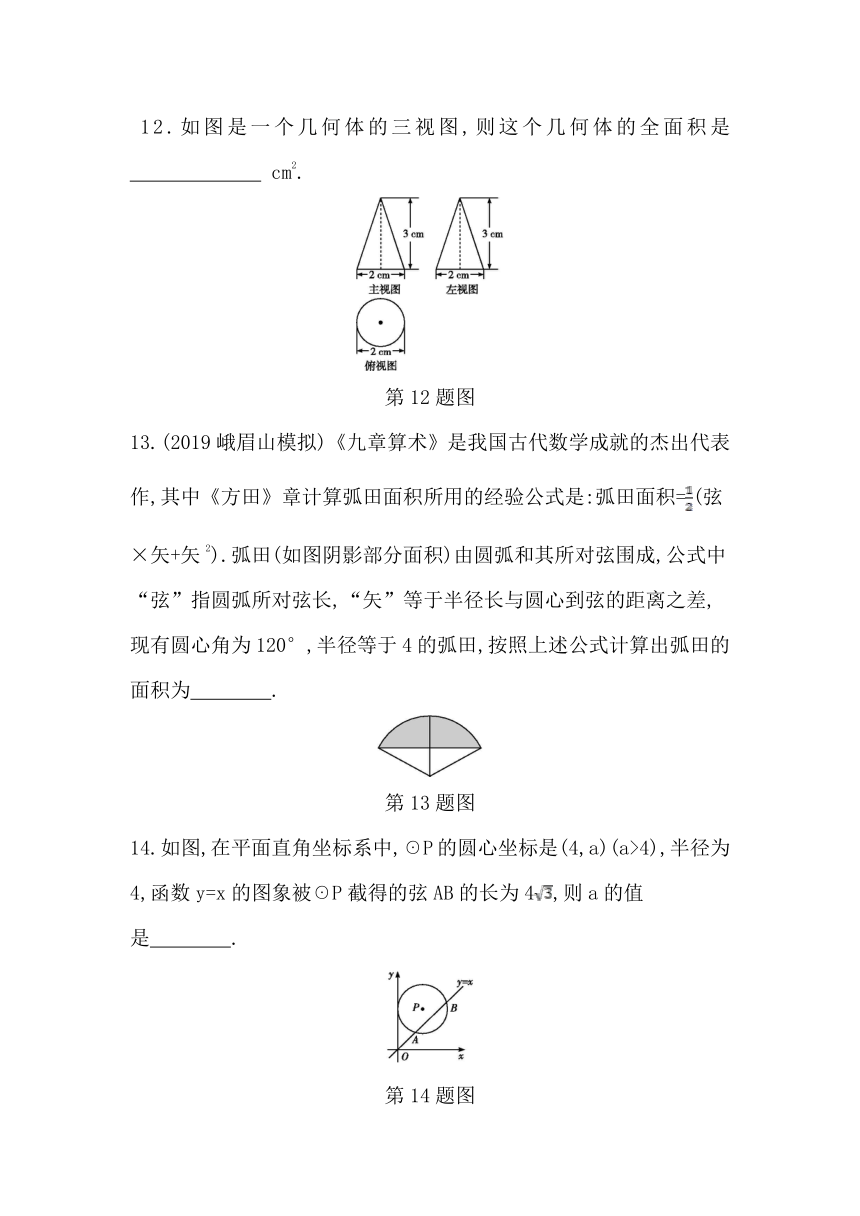
12.如图是一个几何体的三视图,则这个几何体的全面积是
cm2.?
第12题图
13.(2019峨眉山模拟)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢2).弧田(如图阴影部分面积)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为120°,半径等于4的弧田,按照上述公式计算出弧田的面积为 .?
第13题图
14.如图,在平面直角坐标系中,☉P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被☉P截得的弦AB的长为4,则a的值是 .?
第14题图
三、解答题(共44分)
15.(6分)如图,正方形ABCD内接于☉O,M为的中点,连结AM,BM,求证:AM=BM.
16.(6分)如图,☉O的周长等于8π cm,正六边形ABCDEF内接于☉O.
(1)求圆心O到CD的距离;
(2)求正六边形ABCDEF的面积.
17.(8分)如图,AB是☉O的直径,C,D两点在☉O上,若∠C=45°,
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求☉O的半径.
18.(8分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O与AB边交于点D,过点D作☉O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
19.(8分)如图,已知在Rt△ABC中,∠ABC=90°,以AB为直径的☉O与AC交于点D,点E是BC的中点,连结BD,DE.
(1)若=,求sin C;
(2)求证:DE是☉O的切线.
20.(8分)(2018泰州)如图,AB为☉O的直径,C为☉O上一点,∠ABC的平分线交☉O于点D,DE⊥BC于点E.
(1)试判断DE与☉O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
附加题(共10分)
21.(10分)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式——海伦公式S=(其中a,b,c是三角形的三边长,p=,S为三角形的面积),并给出了证明.
例如:在△ABC中,a=3,b=4,c=5,
那么它的面积可以这样计算:
因为a=3,b=4,c=5,
所以p==6,
所以S=
=
=6.
如图,在△ABC中,BC=5,AC=6,AB=9,
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
第27章 检测试题
【测控导航表】
知识点 题号
圆的性质 2,5,9,11,15,17
与圆有关的位置关系 1,4,6,10,12,14,18,19,20
圆的有关计算 3,7,8,12,13,16,20
一、选择题
1.D 解析:因为☉O的直径为10,所以☉O的半径为5.
因为OP=3<5,所以点P与☉O的位置关系是点在圆内.故选D.
2.D 解析:因为AB⊥CD,所以=,CE=DE,
所以∠BOC=2∠BAD=40°,
所以∠OCE=90°-40°=50°.故选D.
3.B 解析:设底面圆的周长为l,根据题意,得×10l=60π,所以l=12π.故选B.
4.A 解析:
连结OB,
因为AB与☉O相切,
所以∠ABO=90°,
因为∠A=30°,
所以∠AOB=60°,
所以∠C=30°,故选A.
5.B 解析:因为AB是☉O的直径,
所以∠ACB=90°.
所以∠CAB+∠B=90°,
因为∠B=3∠BAC,
所以3∠BAC+∠BAC=90°,∠BAC=22.5°,
所以∠B=67.5°.
因为四边形ABCD内接于☉O,
所以∠ADC=180°-∠B=112.5°.故选B.
6.B 解析:如图,连结BD.
因为四边形BCDE为矩形,
所以∠BCD=90°,
所以BD是直径.
因为△ABC是☉O的内接等边三角形,
所以∠BAC=60°,
所以∠BDC=60°,∠DBC=30°,
所以CD=BD=1,
所以BC=CD=,
所以这个矩形的面积为.故选B.
7.B 解析:如图,正六边形ABCDEF中,O是中心,OH是边心距,
连结OA,OB,得∠AOB=60°,
所以△OAB为等边三角形,进而得到△OAH为直角三角形且∠AOH=
30°.
因为OH=,所以AH=1,AB=2.故选B.
8.B 解析:根据题意得l1==,l2==,l3===π,
则l2 019==673 π.故选B.
二、填空题
9.65 解析:因为AB是直径,
所以∠ACB=90°.
所以∠ACD=∠ACB-∠BCD=90°-25°=65°,所以∠ABD=∠ACD=65°.
10.50° 解析:分别连结OA,OB,
因为PA,PB切☉O于点A,B,
所以OA⊥PA,OB⊥PB,
所以∠PAO=∠PBO=90°,
所以∠P+∠AOB=180°,
因为∠ACB=65°,
所以∠AOB=130°,
所以∠P=180°-130°=50°.
11.10 解析:因为OC⊥AB,
所以AD=AB=8,∠ADO=90°.
设CO=x,则AO=x,DO=x-4,在Rt△ADO中,AO2=AD2+OD2,
即x2=82+(x-4)2,解得x=10.所以CO=10.
12.(+1)π 解析:由三视图可知,此几何体为圆锥,其底面半径为1 cm,高为3 cm,由勾股定理得圆锥母线长l==(cm).
所以S侧=πrl=π×1×=π(cm2).
S全=S底+S侧=π+π=(+1)π(cm2).
13.4+2 解析:如图,由题意可得OA=4.
因为∠AOB=120°,所以∠AOD=60°,OD=2,AD=2,矢=CD=4-2=2.
因为OC⊥AB,所以AB=2AD=4.
所以弧田面积=(弦×矢+矢2)=(4×2+22)=4+2.
14.4+2 解析:如图,作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,
因为☉P的圆心坐标是(4,a),
所以OC=4,PC=a,把x=4代入y=x得y=4,
所以D点坐标为(4,4),
所以CD=4,
所以△OCD为等腰直角三角形,
因为PE⊥AB,
所以△PED也为等腰直角三角形,
所以AE=BE=AB=×4=2,
在Rt△PBE中,PB=4,
所以PE==2,
所以PD=PE=2,所以a=4+2.
三、解答题
15.证明:因为四边形ABCD是正方形,
所以AD=BC,
所以=.
因为M为中点,
所以=,
所以+=+,
所以=,
所以AM=BM.
16.解:(1)连结OC,OD,作OH⊥CD于H,
因为☉O的周长等于8π cm,
所以半径OC=4 cm.
因为六边形ABCDEF是正六边形,所以∠COD=60°,
所以∠COH=30°,
所以圆心O到CD的距离为4×cos 30°=2(cm).
(2)正六边形ABCDEF的面积为×4×2×6=24(cm2).
17.解:(1)因为AB是☉O的直径,
所以∠ADB=90°.
因为∠A=∠C=45°,
所以∠ABD=90°-∠A=90°-45°=45°.
(2)连结AC,
因为AB是☉O的直径,
所以∠ACB=90°.
因为∠CAB=∠CDB=30°,BC=3,
所以AB=6.
所以☉O的半径为3.
18.(1)证明:如图,连结CD.
因为∠ACB=90°,
所以AC⊥BC,
所以CB为☉O的切线.
又因为DE是☉O的切线,
所以ED=EC.
所以∠CDE=∠DCE.
因为AC为☉O的直径,
所以∠ADC=90°,
所以∠BDC=90°,
所以∠CDE+∠EDB=90°,∠DCE+∠CBD=90°,
所以∠EDB=∠CBD,
所以ED=EB,
所以EB=EC.
(2)解:△ABC为等腰直角三角形.
理由:
因为四边形ODEC为正方形,
所以OC=CE,∠ACB=90°,
因为OC=AC,CE=BC,
所以AC=BC.
所以△ABC为等腰直角三角形.
19.(1)解:因为AB为直径,
所以∠ADB=90°,
所以∠ABD+∠BAD=90°,
因为∠ABC=90°,
所以∠C+∠BAC=90°,
所以∠C=∠ABD,
因为sin ∠ABD==,
所以sin C=.
(2)证明:连结OD,
因为AB是☉O的直径,
所以∠ADB=90°,
所以∠BDC=90°.
因为E为BC的中点,
所以DE=BE=CE,
所以∠EDB=∠EBD.
因为OD=OB,
所以∠ODB=∠OBD.
因为∠ABC=90°,
所以∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=∠ABC=90°,
所以OD⊥DE,
所以DE是☉O的切线.
20.解:
(1)DE与☉O相切.
理由:连结DO,
因为DO=BO,
所以∠ODB=∠OBD.
因为BD平分∠ABC,
所以∠EBD=∠DBO,
所以∠EBD=∠BDO,
所以DO∥BE.
因为DE⊥BC,
所以OD⊥DE,
所以DE与☉O相切.
(2)因为BD平分∠ABC,DE⊥BE,DF⊥AB,
所以DE=DF=3,
因为BE=3,
所以BD==6,
因为sin∠DBF===,
所以∠DBA=30°,
所以∠DOF=60°.
在Rt△OFD中,sin 60°=,tan 60°=,
所以OD==2,OF==.
所以S阴影=S扇形AOD-S△OFD=-××3=2π-.
附加题
21.解:(1)因为BC=5,AC=6,AB=9,
所以p===10,
所以S=
=
=10.
故△ABC的面积为10.
(2)如图,连结AO,BO,CO,
S△ABC=S△OBC+S△OAC+S△OAB
=r(BC+AC+AB),
所以10=r(5+6+9),
解得r=,
故△ABC的内切圆半径r=.
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共32分)
1.☉O的直径为10,点P到圆心O的距离为3,点P与☉O的位置关系是( )
(A)无法确定 (B)点P在☉O外
(C)点P在☉O上 (D)点P在☉O内
2.如图,在☉O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
第2题图
(A)AD=2OB (B)CE=EO
(C)∠OCE=40° (D)∠BOC=2∠BAD
3.圆锥的母线长为10,侧面积为60π,则这个圆锥的底面周长为( )
(A)10π (B)12π (C)16π (D)20π
4.如图,△ABC的边AC与☉O相交于C,D两点,且经过圆心O,边AB与☉O相切,切点为B.已知∠A=30°,则∠C的大小是( )
第4题图
(A)30° (B)45° (C)60° (D)40°
5.如图,四边形ABCD内接于☉O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
第5题图
(A)100° (B)112.5° (C)120° (D)135°
6.如图,☉O的半径为1,△ABC是☉O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( )
第6题图
(A)2 (B) (C) (D)
7.正六边形的边心距为,则该正六边形的边长是( )
(A) (B)2 (C)3 (D)2
8.如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,
l6,….当AB=1时,l2 019等于( )
(A) (B)673π (C) (D)
第8题图
二、填空题(每小题4分,共24分)
9.(2019南陵县模拟)如图,已知AB是☉O的直径,弦CD与AB相交,若∠BCD=25°,则∠ABD= 度.?
第9题图
10.如图所示,PA,PB切☉O于点A,B,点C是☉O上的一点,且∠ACB=
65°,则∠P= .?
第10题图
11.(2019闵行区模拟)如图,在☉O中,半径OC⊥AB,垂足为点D.如果CD=4,AB=16,那么OC= .?
第11题图
12.如图是一个几何体的三视图,则这个几何体的全面积是
cm2.?
第12题图
13.(2019峨眉山模拟)《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积=(弦×矢+矢2).弧田(如图阴影部分面积)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为120°,半径等于4的弧田,按照上述公式计算出弧田的面积为 .?
第13题图
14.如图,在平面直角坐标系中,☉P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被☉P截得的弦AB的长为4,则a的值是 .?
第14题图
三、解答题(共44分)
15.(6分)如图,正方形ABCD内接于☉O,M为的中点,连结AM,BM,求证:AM=BM.
16.(6分)如图,☉O的周长等于8π cm,正六边形ABCDEF内接于☉O.
(1)求圆心O到CD的距离;
(2)求正六边形ABCDEF的面积.
17.(8分)如图,AB是☉O的直径,C,D两点在☉O上,若∠C=45°,
(1)求∠ABD的度数;
(2)若∠CDB=30°,BC=3,求☉O的半径.
18.(8分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O与AB边交于点D,过点D作☉O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
19.(8分)如图,已知在Rt△ABC中,∠ABC=90°,以AB为直径的☉O与AC交于点D,点E是BC的中点,连结BD,DE.
(1)若=,求sin C;
(2)求证:DE是☉O的切线.
20.(8分)(2018泰州)如图,AB为☉O的直径,C为☉O上一点,∠ABC的平分线交☉O于点D,DE⊥BC于点E.
(1)试判断DE与☉O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3,DF=3,求图中阴影部分的面积.
附加题(共10分)
21.(10分)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式——海伦公式S=(其中a,b,c是三角形的三边长,p=,S为三角形的面积),并给出了证明.
例如:在△ABC中,a=3,b=4,c=5,
那么它的面积可以这样计算:
因为a=3,b=4,c=5,
所以p==6,
所以S=
=
=6.
如图,在△ABC中,BC=5,AC=6,AB=9,
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
第27章 检测试题
【测控导航表】
知识点 题号
圆的性质 2,5,9,11,15,17
与圆有关的位置关系 1,4,6,10,12,14,18,19,20
圆的有关计算 3,7,8,12,13,16,20
一、选择题
1.D 解析:因为☉O的直径为10,所以☉O的半径为5.
因为OP=3<5,所以点P与☉O的位置关系是点在圆内.故选D.
2.D 解析:因为AB⊥CD,所以=,CE=DE,
所以∠BOC=2∠BAD=40°,
所以∠OCE=90°-40°=50°.故选D.
3.B 解析:设底面圆的周长为l,根据题意,得×10l=60π,所以l=12π.故选B.
4.A 解析:
连结OB,
因为AB与☉O相切,
所以∠ABO=90°,
因为∠A=30°,
所以∠AOB=60°,
所以∠C=30°,故选A.
5.B 解析:因为AB是☉O的直径,
所以∠ACB=90°.
所以∠CAB+∠B=90°,
因为∠B=3∠BAC,
所以3∠BAC+∠BAC=90°,∠BAC=22.5°,
所以∠B=67.5°.
因为四边形ABCD内接于☉O,
所以∠ADC=180°-∠B=112.5°.故选B.
6.B 解析:如图,连结BD.
因为四边形BCDE为矩形,
所以∠BCD=90°,
所以BD是直径.
因为△ABC是☉O的内接等边三角形,
所以∠BAC=60°,
所以∠BDC=60°,∠DBC=30°,
所以CD=BD=1,
所以BC=CD=,
所以这个矩形的面积为.故选B.
7.B 解析:如图,正六边形ABCDEF中,O是中心,OH是边心距,
连结OA,OB,得∠AOB=60°,
所以△OAB为等边三角形,进而得到△OAH为直角三角形且∠AOH=
30°.
因为OH=,所以AH=1,AB=2.故选B.
8.B 解析:根据题意得l1==,l2==,l3===π,
则l2 019==673 π.故选B.
二、填空题
9.65 解析:因为AB是直径,
所以∠ACB=90°.
所以∠ACD=∠ACB-∠BCD=90°-25°=65°,所以∠ABD=∠ACD=65°.
10.50° 解析:分别连结OA,OB,
因为PA,PB切☉O于点A,B,
所以OA⊥PA,OB⊥PB,
所以∠PAO=∠PBO=90°,
所以∠P+∠AOB=180°,
因为∠ACB=65°,
所以∠AOB=130°,
所以∠P=180°-130°=50°.
11.10 解析:因为OC⊥AB,
所以AD=AB=8,∠ADO=90°.
设CO=x,则AO=x,DO=x-4,在Rt△ADO中,AO2=AD2+OD2,
即x2=82+(x-4)2,解得x=10.所以CO=10.
12.(+1)π 解析:由三视图可知,此几何体为圆锥,其底面半径为1 cm,高为3 cm,由勾股定理得圆锥母线长l==(cm).
所以S侧=πrl=π×1×=π(cm2).
S全=S底+S侧=π+π=(+1)π(cm2).
13.4+2 解析:如图,由题意可得OA=4.
因为∠AOB=120°,所以∠AOD=60°,OD=2,AD=2,矢=CD=4-2=2.
因为OC⊥AB,所以AB=2AD=4.
所以弧田面积=(弦×矢+矢2)=(4×2+22)=4+2.
14.4+2 解析:如图,作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,
因为☉P的圆心坐标是(4,a),
所以OC=4,PC=a,把x=4代入y=x得y=4,
所以D点坐标为(4,4),
所以CD=4,
所以△OCD为等腰直角三角形,
因为PE⊥AB,
所以△PED也为等腰直角三角形,
所以AE=BE=AB=×4=2,
在Rt△PBE中,PB=4,
所以PE==2,
所以PD=PE=2,所以a=4+2.
三、解答题
15.证明:因为四边形ABCD是正方形,
所以AD=BC,
所以=.
因为M为中点,
所以=,
所以+=+,
所以=,
所以AM=BM.
16.解:(1)连结OC,OD,作OH⊥CD于H,
因为☉O的周长等于8π cm,
所以半径OC=4 cm.
因为六边形ABCDEF是正六边形,所以∠COD=60°,
所以∠COH=30°,
所以圆心O到CD的距离为4×cos 30°=2(cm).
(2)正六边形ABCDEF的面积为×4×2×6=24(cm2).
17.解:(1)因为AB是☉O的直径,
所以∠ADB=90°.
因为∠A=∠C=45°,
所以∠ABD=90°-∠A=90°-45°=45°.
(2)连结AC,
因为AB是☉O的直径,
所以∠ACB=90°.
因为∠CAB=∠CDB=30°,BC=3,
所以AB=6.
所以☉O的半径为3.
18.(1)证明:如图,连结CD.
因为∠ACB=90°,
所以AC⊥BC,
所以CB为☉O的切线.
又因为DE是☉O的切线,
所以ED=EC.
所以∠CDE=∠DCE.
因为AC为☉O的直径,
所以∠ADC=90°,
所以∠BDC=90°,
所以∠CDE+∠EDB=90°,∠DCE+∠CBD=90°,
所以∠EDB=∠CBD,
所以ED=EB,
所以EB=EC.
(2)解:△ABC为等腰直角三角形.
理由:
因为四边形ODEC为正方形,
所以OC=CE,∠ACB=90°,
因为OC=AC,CE=BC,
所以AC=BC.
所以△ABC为等腰直角三角形.
19.(1)解:因为AB为直径,
所以∠ADB=90°,
所以∠ABD+∠BAD=90°,
因为∠ABC=90°,
所以∠C+∠BAC=90°,
所以∠C=∠ABD,
因为sin ∠ABD==,
所以sin C=.
(2)证明:连结OD,
因为AB是☉O的直径,
所以∠ADB=90°,
所以∠BDC=90°.
因为E为BC的中点,
所以DE=BE=CE,
所以∠EDB=∠EBD.
因为OD=OB,
所以∠ODB=∠OBD.
因为∠ABC=90°,
所以∠EDO=∠EDB+∠ODB=∠EBD+∠OBD=∠ABC=90°,
所以OD⊥DE,
所以DE是☉O的切线.
20.解:
(1)DE与☉O相切.
理由:连结DO,
因为DO=BO,
所以∠ODB=∠OBD.
因为BD平分∠ABC,
所以∠EBD=∠DBO,
所以∠EBD=∠BDO,
所以DO∥BE.
因为DE⊥BC,
所以OD⊥DE,
所以DE与☉O相切.
(2)因为BD平分∠ABC,DE⊥BE,DF⊥AB,
所以DE=DF=3,
因为BE=3,
所以BD==6,
因为sin∠DBF===,
所以∠DBA=30°,
所以∠DOF=60°.
在Rt△OFD中,sin 60°=,tan 60°=,
所以OD==2,OF==.
所以S阴影=S扇形AOD-S△OFD=-××3=2π-.
附加题
21.解:(1)因为BC=5,AC=6,AB=9,
所以p===10,
所以S=
=
=10.
故△ABC的面积为10.
(2)如图,连结AO,BO,CO,
S△ABC=S△OBC+S△OAC+S△OAB
=r(BC+AC+AB),
所以10=r(5+6+9),
解得r=,
故△ABC的内切圆半径r=.
