2020年春华师大版八下数学18.2平行四边形的判定(第一课时)教学课件(17张)
文档属性
| 名称 | 2020年春华师大版八下数学18.2平行四边形的判定(第一课时)教学课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 22:56:10 | ||
图片预览





文档简介
课件17张PPT。知识要点1.两组对边分别相等的四边形是平行四边形2.一组对边平行且相等的四边形是
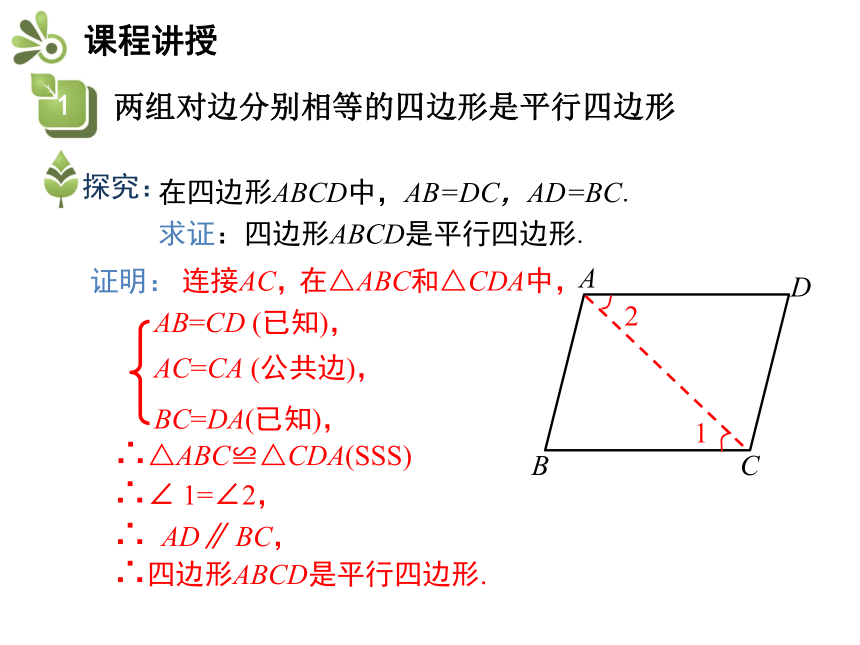
平行四边形BADC四边形ABCD是平行四边形,为什么?在四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形.连接AC,在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC≌△CDA(SSS)∴∠ 1=∠2,∴ AD∥ BC,∴四边形ABCD是平行四边形.证明:21ABCD练一练:如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.练一练:∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.证明:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证: 四边形ABCD是平行四边形.证明:连接AC.
∵AB∥CD, ∴∠1=∠2.AB=CD, AC=CA,∠1=∠2,∴△ABC≌△CDA(SAS),∴∠BCA=∠DAC ,∴AD∥BC∴四边形ABCD是平行四边形.例 如图,点E,F在□ABCD的边BC,AD上,BE= BC,FD= AD,连接BF,DE.
求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥ BC,AD=BC.
∵BE= BC,FD= AD,
∴BE =FD .又∵BE∥FD,
∴四边形EBFD是平行四边形.AFEDCB练一练:(中考·衡阳)如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥ADB1. 四边形的四条边长分别是a,b,c,d,其中a,b为
一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形B2.如图,在□ABCD中,点E,F分别在AD,BC上,若要
使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③C3.如图,在平行四边形ABCD中,点E,F分别在AB,
CD上,AE=CF,连接AF,BF,DE,CE,分别交于
点H,G.求证:
(1)四边形AECF是平行四边形;
(2)EF与GH互相平分.
证明:(1)∵四边形ABCD是平
行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴四边形AECF是平行四边形.(2)由(1),得四边形AECF是平行四边形,
∴AF∥CE,
∵AE=CF,AB∥CD,AB=CD,
∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,
∴BF∥DE,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分.平行四边形的判定定理1,2一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形
平行四边形BADC四边形ABCD是平行四边形,为什么?在四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形.连接AC,在△ABC和△CDA中,AB=CD (已知),BC=DA(已知),AC=CA (公共边),∴△ABC≌△CDA(SSS)∴∠ 1=∠2,∴ AD∥ BC,∴四边形ABCD是平行四边形.证明:21ABCD练一练:如图,分别以△ABC的三边为一边,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.
求证:四边形ADEF是平行四边形.练一练:∵△ABD,△BCE,△ACF都为等边三角形,
∴DB=AB=AD,BE=BC,AC=AF,
∠DBA=60°,∠EBC=60°.
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,∴△DBE≌△ABC,
∴DE=AC.又∵AC=AF,∴AF=DE.
同理可证:△ABC≌△FEC,∴AB=FE,∴FE=AD,
∴四边形ADEF是平行四边形.证明:如图,在四边形ABCD中,AB=CD,AB∥CD.
求证: 四边形ABCD是平行四边形.证明:连接AC.
∵AB∥CD, ∴∠1=∠2.AB=CD, AC=CA,∠1=∠2,∴△ABC≌△CDA(SAS),∴∠BCA=∠DAC ,∴AD∥BC∴四边形ABCD是平行四边形.例 如图,点E,F在□ABCD的边BC,AD上,BE= BC,FD= AD,连接BF,DE.
求证:四边形BEDF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥ BC,AD=BC.
∵BE= BC,FD= AD,
∴BE =FD .又∵BE∥FD,
∴四边形EBFD是平行四边形.AFEDCB练一练:(中考·衡阳)如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,下列可添加的条件不正确的是( )
A.AB=CD
B.BC=AD
C.∠A=∠C
D.BC∥ADB1. 四边形的四条边长分别是a,b,c,d,其中a,b为
一组对边长,c,d为另一组对边长且a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D.对角线垂直的四边形B2.如图,在□ABCD中,点E,F分别在AD,BC上,若要
使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③C3.如图,在平行四边形ABCD中,点E,F分别在AB,
CD上,AE=CF,连接AF,BF,DE,CE,分别交于
点H,G.求证:
(1)四边形AECF是平行四边形;
(2)EF与GH互相平分.
证明:(1)∵四边形ABCD是平
行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴四边形AECF是平行四边形.(2)由(1),得四边形AECF是平行四边形,
∴AF∥CE,
∵AE=CF,AB∥CD,AB=CD,
∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,
∴BF∥DE,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分.平行四边形的判定定理1,2一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形
