青岛版七年级数学下册第8章角的单元测试卷(附图片答案)
文档属性
| 名称 | 青岛版七年级数学下册第8章角的单元测试卷(附图片答案) |  | |
| 格式 | zip | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-15 23:25:32 | ||
图片预览

文档简介
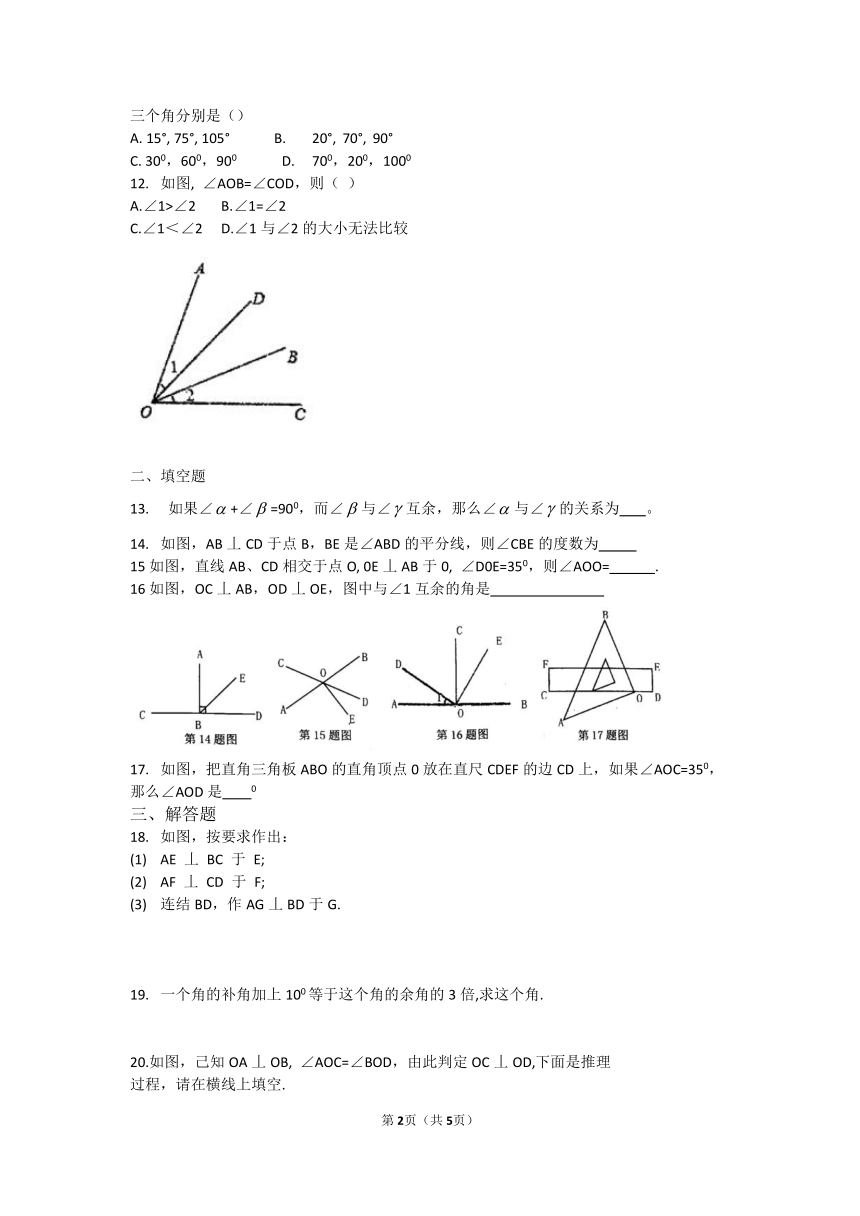
青岛版数学七年级下册第八章测试卷
一、选择题
1下列时刻中,时针与分针之间的夹角为300的是( )
A早晨6点 B.下午13点 C.中午12点 D.上午9点
2.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落 E
在D'、C'的位置.若∠AE D'=50°,则∠DEF等于( )
A.50° B.65° C.75° D.60°
3将31.62°化成度分秒表示,结果是( )
A.3106'2'' B.31037'12"
C.31037'2" D.31°37'
4. 如图∠AOC和∠BOD都是直角,如果∠AOB=140°,则∠DOC的度数
A.300 B.400 C.500 D.600
5. 如果∠=260,那么∠余角的补角等于()
A.20° B .700 C.110° D.1160
6. 下列说法中正确的有()
(1) 钝角的补角一定是锐角
(2) 过己知直线外一点作这条直线的垂线有且只有一条
(3) —个角的两个邻补角是对顶角
(4) 等角的补角相等
(5) 直线外一点A与直线上各点连接而成的所有线段中,最短线段的长是3cm,则
点A到直线的距离是3cm .
A 2个 B. 3个 C. 4 个 D. 5 个?
7. 如图,直线a、b、c两两相交,若∠1+∠7=180。,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
8. 如图,P0丄OR, 0Q丄PR,能表示点到直线(或线段)的距离的线段有( )
A. 1条 B.2条 C.3条 D.5条
9. 如图,已知ON丄a,OM丄a,所以OM与ON重合的理由是( ).
A. 两点确定一条直线
B. 经过一点有且只有一条线段垂直于己知直线
C. 过一点只能作一条垂线
D. 垂线段最短
10. 如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是()
A. ∠1 B∠2 C. ∠1-∠2) D. (∠l+∠2)
11. 如果∠A和∠B互为余角,∠B和∠C互为补角,∠A与∠C的和等于1200,那么这
三个角分别是()
A. 15°, 75°, 105° B. 20°, 70°, 90°
C. 300,600,900 D. 700,200,1000
12. 如图, ∠AOB=∠COD,则( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1与∠2的大小无法比较
二、填空题
13. 如果∠+∠=900,而∠与∠互余,那么∠与∠的关系为 。
14. 如图,AB丄CD于点B,BE是∠ABD的平分线,则∠CBE的度数为
15如图,直线AB、CD相交于点O, 0E丄AB于0, ∠D0E=350,则∠AOO= .?
16如图,OC丄AB,OD丄OE,图中与∠1互余的角是
17. 如图,把直角三角板ABO的直角顶点0放在直尺CDEF的边CD上,如果∠AOC=350,
那么∠AOD是 0
三、解答题
18. 如图,按要求作出:
(1) AE 丄 BC 于 E;
(2) AF 丄 CD 于 F;
(3) 连结BD,作AG丄BD于G.
19. 一个角的补角加上100等于这个角的余角的3倍,求这个角.
20.如图,己知OA丄OB, ∠AOC=∠BOD,由此判定OC丄OD,下面是推理
过程,请在横线上填空.
OA丄OB(己知)
=90° ( )
∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC
∠AOC=∠BOD
∠AOB=∠COD (等式的性质)
=90°
CO 丄 OD ( )
21.如图,直线BC与MN相交于点O,AO丄OC,.OE平分∠BON,若∠EON=2 0°,
求∠AOM 的度数。
22. 如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入
围墙,只能站在墙外。如何测量(运用本章知识)??
23. 如图,AO丄BO, CO丄DO,若∠BOC: ∠AOC=1: 5,求∠AOD 的度数
24.如图vO 是直线 AB、CD 的交点,∠AOE=∠COF=900,∠EOF =320.
(1)求∠AOC的度数;(2)求∠AOD的度数.
25.如图,数一数以O为顶点且小于1800的角一共有多少个?若图中有n条射线,
你能得到解这类问题的一般方法吗?
一、选择题
1下列时刻中,时针与分针之间的夹角为300的是( )
A早晨6点 B.下午13点 C.中午12点 D.上午9点
2.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落 E
在D'、C'的位置.若∠AE D'=50°,则∠DEF等于( )
A.50° B.65° C.75° D.60°
3将31.62°化成度分秒表示,结果是( )
A.3106'2'' B.31037'12"
C.31037'2" D.31°37'
4. 如图∠AOC和∠BOD都是直角,如果∠AOB=140°,则∠DOC的度数
A.300 B.400 C.500 D.600
5. 如果∠=260,那么∠余角的补角等于()
A.20° B .700 C.110° D.1160
6. 下列说法中正确的有()
(1) 钝角的补角一定是锐角
(2) 过己知直线外一点作这条直线的垂线有且只有一条
(3) —个角的两个邻补角是对顶角
(4) 等角的补角相等
(5) 直线外一点A与直线上各点连接而成的所有线段中,最短线段的长是3cm,则
点A到直线的距离是3cm .
A 2个 B. 3个 C. 4 个 D. 5 个?
7. 如图,直线a、b、c两两相交,若∠1+∠7=180。,则图中与∠1互补的角有( )
A. 1个 B. 2个 C. 3个 D. 4个
8. 如图,P0丄OR, 0Q丄PR,能表示点到直线(或线段)的距离的线段有( )
A. 1条 B.2条 C.3条 D.5条
9. 如图,已知ON丄a,OM丄a,所以OM与ON重合的理由是( ).
A. 两点确定一条直线
B. 经过一点有且只有一条线段垂直于己知直线
C. 过一点只能作一条垂线
D. 垂线段最短
10. 如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是()
A. ∠1 B∠2 C. ∠1-∠2) D. (∠l+∠2)
11. 如果∠A和∠B互为余角,∠B和∠C互为补角,∠A与∠C的和等于1200,那么这
三个角分别是()
A. 15°, 75°, 105° B. 20°, 70°, 90°
C. 300,600,900 D. 700,200,1000
12. 如图, ∠AOB=∠COD,则( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1与∠2的大小无法比较
二、填空题
13. 如果∠+∠=900,而∠与∠互余,那么∠与∠的关系为 。
14. 如图,AB丄CD于点B,BE是∠ABD的平分线,则∠CBE的度数为
15如图,直线AB、CD相交于点O, 0E丄AB于0, ∠D0E=350,则∠AOO= .?
16如图,OC丄AB,OD丄OE,图中与∠1互余的角是
17. 如图,把直角三角板ABO的直角顶点0放在直尺CDEF的边CD上,如果∠AOC=350,
那么∠AOD是 0
三、解答题
18. 如图,按要求作出:
(1) AE 丄 BC 于 E;
(2) AF 丄 CD 于 F;
(3) 连结BD,作AG丄BD于G.
19. 一个角的补角加上100等于这个角的余角的3倍,求这个角.
20.如图,己知OA丄OB, ∠AOC=∠BOD,由此判定OC丄OD,下面是推理
过程,请在横线上填空.
OA丄OB(己知)
=90° ( )
∠AOB=∠AOC-∠BOC, ∠COD=∠BOD-∠BOC
∠AOC=∠BOD
∠AOB=∠COD (等式的性质)
=90°
CO 丄 OD ( )
21.如图,直线BC与MN相交于点O,AO丄OC,.OE平分∠BON,若∠EON=2 0°,
求∠AOM 的度数。
22. 如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入
围墙,只能站在墙外。如何测量(运用本章知识)??
23. 如图,AO丄BO, CO丄DO,若∠BOC: ∠AOC=1: 5,求∠AOD 的度数
24.如图vO 是直线 AB、CD 的交点,∠AOE=∠COF=900,∠EOF =320.
(1)求∠AOC的度数;(2)求∠AOD的度数.
25.如图,数一数以O为顶点且小于1800的角一共有多少个?若图中有n条射线,
你能得到解这类问题的一般方法吗?
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
