青岛版数学七年级下册第十三章测试卷(word版含解析)
文档属性
| 名称 | 青岛版数学七年级下册第十三章测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览



文档简介
青岛版数学七年级下册第十三章测试卷
一、选择题
1.下列长度的三根木棒首尾相接,不能做成三角形框架的是( ???)
A.?5cm,7cm,10cm????????????????????????????????????????????B.?5cm,7cm,13cm C.?7cm,10cm,13cm??????????????????????????????????????????D.?5cm,10cm,13cm
2.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为(?? )
A.?7????????????????????????????????????B.?7或8????????????????????????????????????C.?8或9????????????????????????????????????D.?7或8或9
3.将一副三角板按如图方式叠放,则 的度数是(??? ).
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
4.试通过画图来判定,下列说法正确的是( )
A.?一个直角三角形一定不是等腰三角形??????????????????B.?一个等腰三角形一定不是锐角三角形 C.?一个钝角三角形一定不是等腰三角形??????????????????D.?一个等边三角形一定不是钝角三角形
5.下列说法中正确的是( )
A.?三角形三条高所在的直线交于一点 B.?有且只有一条直线与已知直线平行 C.?垂直于同一条直线的两条直线互相垂直 D.?从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
6.如图,工人师傅安装门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的依据是(?? )
A.两点之间线段最短 B.两点确定一条直线 C.垂线段最短 D.三角形的稳定性
7.一个正n边形的每个外角均为40°,则n=( )
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
8.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(?? )
A.?A,C两点之间??????????????? ??B.?E,G两点之间????????????
?????C.?B,F两点之间?????????????????D.?G,H两点之间
9.正多边形的一个内角为140°,则该正多边形的边数为(?? )
A.?9???????????????????????????????????????????B.?8???????????????????????????????????????????C.?7???????????????????????????????????????????D.?4
10.满足下列条件的△ABC中,不是直角三角形的是(???)
A.?∠B+∠A=∠C???????????????????????????????????????????????????????B.?∠A:∠B:∠C=2:3:5 C.?∠A=2∠B=3∠C???????????????????????????????????????????????????D.?一个外角等于和它相邻的一个内角
11.如图,直角△ADB中,∠D=90°,C为AD上一点,且∠ACB的度数为(5x-10)°,则x的值可能是
A.?10 ??????????????????????????????????????B.?20??????????????????????????????????????C.?30??????????????????????????????????????D.?40
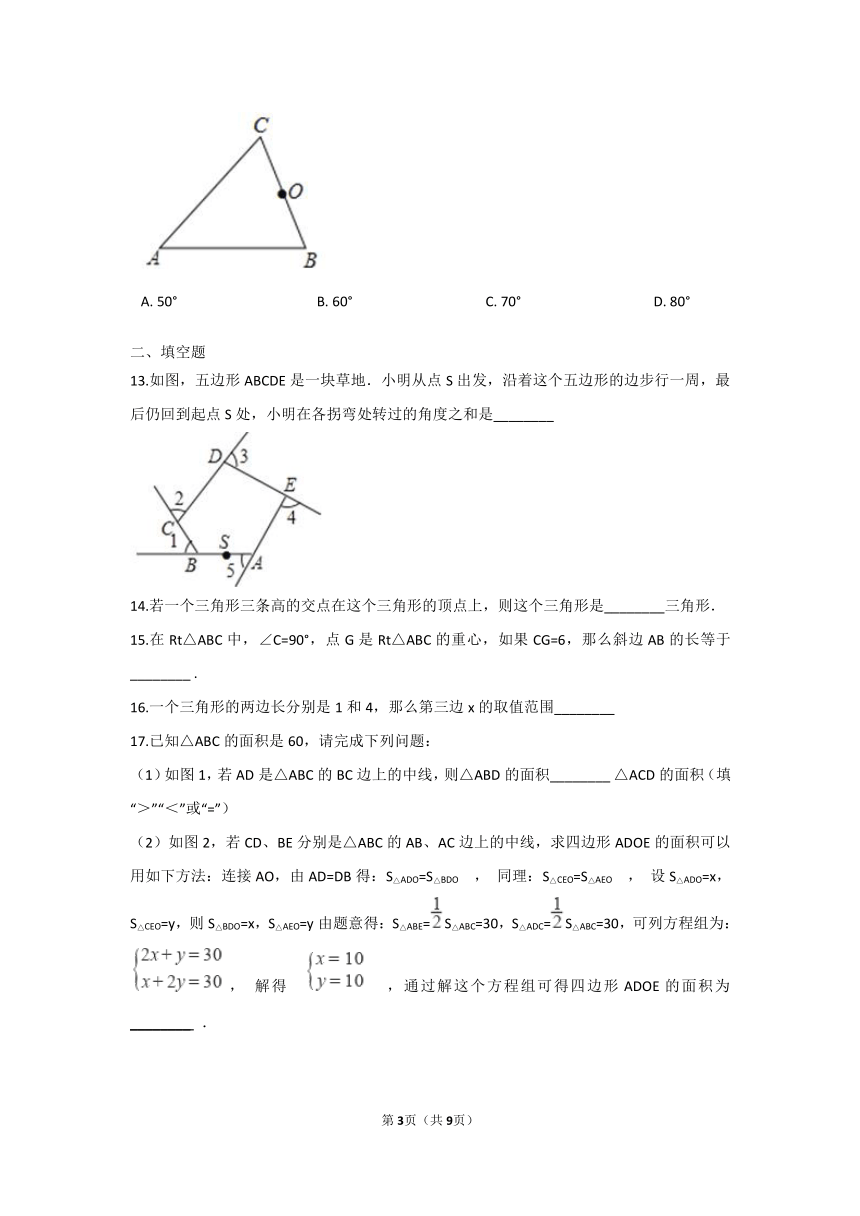
12.如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( ) ?
A.?50°????????????????????????????????????????B.?60°??????????????????????????????????????C.?70°??????????????????????????????????????D.?80°
二、填空题
13.如图,五边形ABCDE是一块草地.小明从点S出发,沿着这个五边形的边步行一周,最后仍回到起点S处,小明在各拐弯处转过的角度之和是________?
14.若一个三角形三条高的交点在这个三角形的顶点上,则这个三角形是________三角形.
15.在Rt△ABC中,∠C=90°,点G是Rt△ABC的重心,如果CG=6,那么斜边AB的长等于________ .
16.一个三角形的两边长分别是1和4,那么第三边x的取值范围________
17.已知△ABC的面积是60,请完成下列问题: (1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积________?△ACD的面积(填“>”“<”或“=”) (2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO , 同理:S△CEO=S△AEO , 设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=S△ABC=30,S△ADC=S△ABC=30,可列方程组为:, 解得 ,通过解这个方程组可得四边形ADOE的面积为________? .
18.一个三角形的两条边长度分别为1和4,则第三边a可取________.(填一个满足条件的数)
19.如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=________.
20.如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为________.
21.有四根细木棒,长度分别为 3cm、5cm、7cm、9cm,以其中任意三条为边可以构成________个三角形.
22.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E 运动,最终到达点E.若点P运动的时间为x秒,那么当x=________时,△APE的面积等于5.
三、解答题
23.已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边长.
24.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
25.(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近; (2)如果甲、乙走的路程图改成图2,两人走的路程远近相同吗? ?
26.如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
27.如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
参考答案
一、选择题
B D D D A D D B A C C D
二、填空题
13. 360°
14. 直角
15. 18
16. 大于3小于5
17. =;20
18. (答案不唯一) 如4
19. 2
20. 3,9,15
21. 3
22. 或5
三、解答题
23. 解:依题意有n﹣3=4, 解得n=7, 设最短边为x,则 7x+1+2+3+4+5+6=56, 解得x=5. 故这个多边形的各边长是5,6,7,8,9,10,11.
24. 解:设∠1=∠2=x,则∠3=∠4=2x. 因为∠BAC=63°, 所以∠2+∠4=117°,即x+2x=117°, 所以x=39°; 所以∠3=∠4=78°, ∠DAC=180°﹣∠3﹣∠4=24°.
25. 解:(1)BC=AB﹣AC=10, 甲所走的路径长=?2?π?=?2?π?=20π(m), 乙所走的路径长=?2?π?+?2?π?=?2?π?+?π?=20π(m), 所以两人所走路程的相等; (2)两人走的路程远近相同.理由如下:甲所走的路径长=?2?π?=π?AB, 乙所走的路径长=?2?π?+?2?π?+?π?=π(AC+CD+DB)=π?AB, 即两人走的路程远近相同.
26. (1)解:∵BE⊥AC,∠ACB=70°, ∴∠EBC=90°﹣70°=20°, ∵CD⊥AB,∠ABC=40°, ∴∠DCB=90°﹣40°=50°, ∴∠BHC=180°﹣20°﹣50°=110°. (2)解:∵BE平分∠ABC,∠ABC=40°, ∴∠EBC=20°, ∵DC平分∠ACB,∠ACB=70°, ∴∠DCB=35°, ∴∠BHC=180°﹣20°﹣35°=125°
27. (1)解:∵∠B=40°,∠C=70°, ∴∠BAC=70°. ∵CF平分∠DCE, ∴∠BAD=∠CAD=35°, ∴∠ADE=∠B+∠BAD=75°. ∵AE⊥BC, ∴∠AEB=90°, ∴∠DAE=90°﹣∠ADE=15° (2)解:同(1),可得∠ADE=75°. ∵FE⊥BC, ∴∠FEB=90°, ∴∠DFE=90°﹣∠ADE=15°
一、选择题
1.下列长度的三根木棒首尾相接,不能做成三角形框架的是( ???)
A.?5cm,7cm,10cm????????????????????????????????????????????B.?5cm,7cm,13cm C.?7cm,10cm,13cm??????????????????????????????????????????D.?5cm,10cm,13cm
2.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为(?? )
A.?7????????????????????????????????????B.?7或8????????????????????????????????????C.?8或9????????????????????????????????????D.?7或8或9
3.将一副三角板按如图方式叠放,则 的度数是(??? ).
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
4.试通过画图来判定,下列说法正确的是( )
A.?一个直角三角形一定不是等腰三角形??????????????????B.?一个等腰三角形一定不是锐角三角形 C.?一个钝角三角形一定不是等腰三角形??????????????????D.?一个等边三角形一定不是钝角三角形
5.下列说法中正确的是( )
A.?三角形三条高所在的直线交于一点 B.?有且只有一条直线与已知直线平行 C.?垂直于同一条直线的两条直线互相垂直 D.?从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
6.如图,工人师傅安装门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的依据是(?? )
A.两点之间线段最短 B.两点确定一条直线 C.垂线段最短 D.三角形的稳定性
7.一个正n边形的每个外角均为40°,则n=( )
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
8.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在(?? )
A.?A,C两点之间??????????????? ??B.?E,G两点之间????????????
?????C.?B,F两点之间?????????????????D.?G,H两点之间
9.正多边形的一个内角为140°,则该正多边形的边数为(?? )
A.?9???????????????????????????????????????????B.?8???????????????????????????????????????????C.?7???????????????????????????????????????????D.?4
10.满足下列条件的△ABC中,不是直角三角形的是(???)
A.?∠B+∠A=∠C???????????????????????????????????????????????????????B.?∠A:∠B:∠C=2:3:5 C.?∠A=2∠B=3∠C???????????????????????????????????????????????????D.?一个外角等于和它相邻的一个内角
11.如图,直角△ADB中,∠D=90°,C为AD上一点,且∠ACB的度数为(5x-10)°,则x的值可能是
A.?10 ??????????????????????????????????????B.?20??????????????????????????????????????C.?30??????????????????????????????????????D.?40
12.如图,△ABC中,∠A=50°,O是BC的中点,以O为圆心,OB长为半径画弧,分别交AB,AC于点D,E,连接OD,OE,测量∠DOE的度数是( ) ?
A.?50°????????????????????????????????????????B.?60°??????????????????????????????????????C.?70°??????????????????????????????????????D.?80°
二、填空题
13.如图,五边形ABCDE是一块草地.小明从点S出发,沿着这个五边形的边步行一周,最后仍回到起点S处,小明在各拐弯处转过的角度之和是________?
14.若一个三角形三条高的交点在这个三角形的顶点上,则这个三角形是________三角形.
15.在Rt△ABC中,∠C=90°,点G是Rt△ABC的重心,如果CG=6,那么斜边AB的长等于________ .
16.一个三角形的两边长分别是1和4,那么第三边x的取值范围________
17.已知△ABC的面积是60,请完成下列问题: (1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积________?△ACD的面积(填“>”“<”或“=”) (2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO , 同理:S△CEO=S△AEO , 设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=S△ABC=30,S△ADC=S△ABC=30,可列方程组为:, 解得 ,通过解这个方程组可得四边形ADOE的面积为________? .
18.一个三角形的两条边长度分别为1和4,则第三边a可取________.(填一个满足条件的数)
19.如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=________.
20.如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为________.
21.有四根细木棒,长度分别为 3cm、5cm、7cm、9cm,以其中任意三条为边可以构成________个三角形.
22.如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E 运动,最终到达点E.若点P运动的时间为x秒,那么当x=________时,△APE的面积等于5.
三、解答题
23.已知从n边形的一个顶点出发共有4条对角线,其周长为56,且各边长是连续的自然数,求这个多边形的各边长.
24.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
25.(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近; (2)如果甲、乙走的路程图改成图2,两人走的路程远近相同吗? ?
26.如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
27.如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
参考答案
一、选择题
B D D D A D D B A C C D
二、填空题
13. 360°
14. 直角
15. 18
16. 大于3小于5
17. =;20
18. (答案不唯一) 如4
19. 2
20. 3,9,15
21. 3
22. 或5
三、解答题
23. 解:依题意有n﹣3=4, 解得n=7, 设最短边为x,则 7x+1+2+3+4+5+6=56, 解得x=5. 故这个多边形的各边长是5,6,7,8,9,10,11.
24. 解:设∠1=∠2=x,则∠3=∠4=2x. 因为∠BAC=63°, 所以∠2+∠4=117°,即x+2x=117°, 所以x=39°; 所以∠3=∠4=78°, ∠DAC=180°﹣∠3﹣∠4=24°.
25. 解:(1)BC=AB﹣AC=10, 甲所走的路径长=?2?π?=?2?π?=20π(m), 乙所走的路径长=?2?π?+?2?π?=?2?π?+?π?=20π(m), 所以两人所走路程的相等; (2)两人走的路程远近相同.理由如下:甲所走的路径长=?2?π?=π?AB, 乙所走的路径长=?2?π?+?2?π?+?π?=π(AC+CD+DB)=π?AB, 即两人走的路程远近相同.
26. (1)解:∵BE⊥AC,∠ACB=70°, ∴∠EBC=90°﹣70°=20°, ∵CD⊥AB,∠ABC=40°, ∴∠DCB=90°﹣40°=50°, ∴∠BHC=180°﹣20°﹣50°=110°. (2)解:∵BE平分∠ABC,∠ABC=40°, ∴∠EBC=20°, ∵DC平分∠ACB,∠ACB=70°, ∴∠DCB=35°, ∴∠BHC=180°﹣20°﹣35°=125°
27. (1)解:∵∠B=40°,∠C=70°, ∴∠BAC=70°. ∵CF平分∠DCE, ∴∠BAD=∠CAD=35°, ∴∠ADE=∠B+∠BAD=75°. ∵AE⊥BC, ∴∠AEB=90°, ∴∠DAE=90°﹣∠ADE=15° (2)解:同(1),可得∠ADE=75°. ∵FE⊥BC, ∴∠FEB=90°, ∴∠DFE=90°﹣∠ADE=15°
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
