青岛版数学七年级下册第十四章测试卷(word版含解析)
文档属性
| 名称 | 青岛版数学七年级下册第十四章测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 43.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 07:59:24 | ||
图片预览


文档简介
青岛版数学七年级下册第十四章测试卷
一、选择题
1.在平面直角坐标系中,点A(-4,0)在( )
A.?x轴正半轴上;?????????????????B.?x轴负半轴上;?????????????????
C.?y轴正半轴上;?????????????????D.?y轴负半轴上
2.点P(m+3,m+1)在直角坐标系的x轴上,则P点的坐标为(? )
A.?(0,﹣2)????????????????????????B.?(2,0)????????????????????????C.?(0,2)????????????????????????D.?(0,﹣4)
3.已知y轴上的点P到原点的距离为5,则点P的坐标为(?? )
A.?(5,0)???????????? B.?(0,5)或(0,﹣5)?????????
???C.?(0,5)????????????D.?(5,0)或(﹣5,0)
4.如图是丁丁画的一张脸的示意图,如果用(0,2)表示靠左边的眼睛,用(2,2)表示靠右边的眼睛,那么嘴的位置可以表示成( )
A.?(1,0)???????????????????????B.?(﹣1,0)???????????????????????C.?(﹣1,1)???????????????????????D.?(1,﹣1)
5.如下图所示,图中是沈阳市地图简图的一部分,图中“故宫”、“鼓楼”所在的区域分别是(??? )
D
E
F
6
鼓楼
大北门
7
故宫
8
大南门
东华门
A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7
6.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是(????? )
A.?(7,0)???????????????????????????B.?(0,7)???????????????????????????C.?(7,7)???????????????????????????D.?(6,0)
7.根据下列表述,能确定具体位置的是(? ??)
A.?某电影院2排???????????????????B.?大桥南路?????????????????
??C.?北偏东30°?????????????????? ?D.?东经108°,北纬43°
8.中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,﹣1)表示“炮”的位置,那么“将”的位置应表示为(?? )
A.?(﹣2,3)??????????????????????B.?(0,﹣5)??????????????????????C.?(﹣3,1)??????????????????????D.?(﹣4,2)
9.已知点P位于y轴的右侧,距y轴5个单位长度,位于x轴上方,距x轴6个单位长度,则点P的坐标是( )
A.?(﹣5,6)????????????????????????B.?(6,5)????????????????????????C.?(﹣6,5)????????????????????????D.?(5,6)
10.若点P在第二象限内,且到x轴的距离是5,到y轴的距离是7,则点P的坐标是(?? )
A.?(﹣7,5)??????????????????????B.?(7,﹣5)??????????????????????C.?(﹣5,7)??????????????????????D.?(5,﹣7)
11.点M到x轴的距离为3,到y的距离为4,则点M的坐标为(????)
A.?(3,4)??????????????????????????????????????????????????B.?(4,3) C.?(4,3),(-4,3)????????????????????????????D.?(4,3),(-4,3),(-4,-3)或(4,-3)
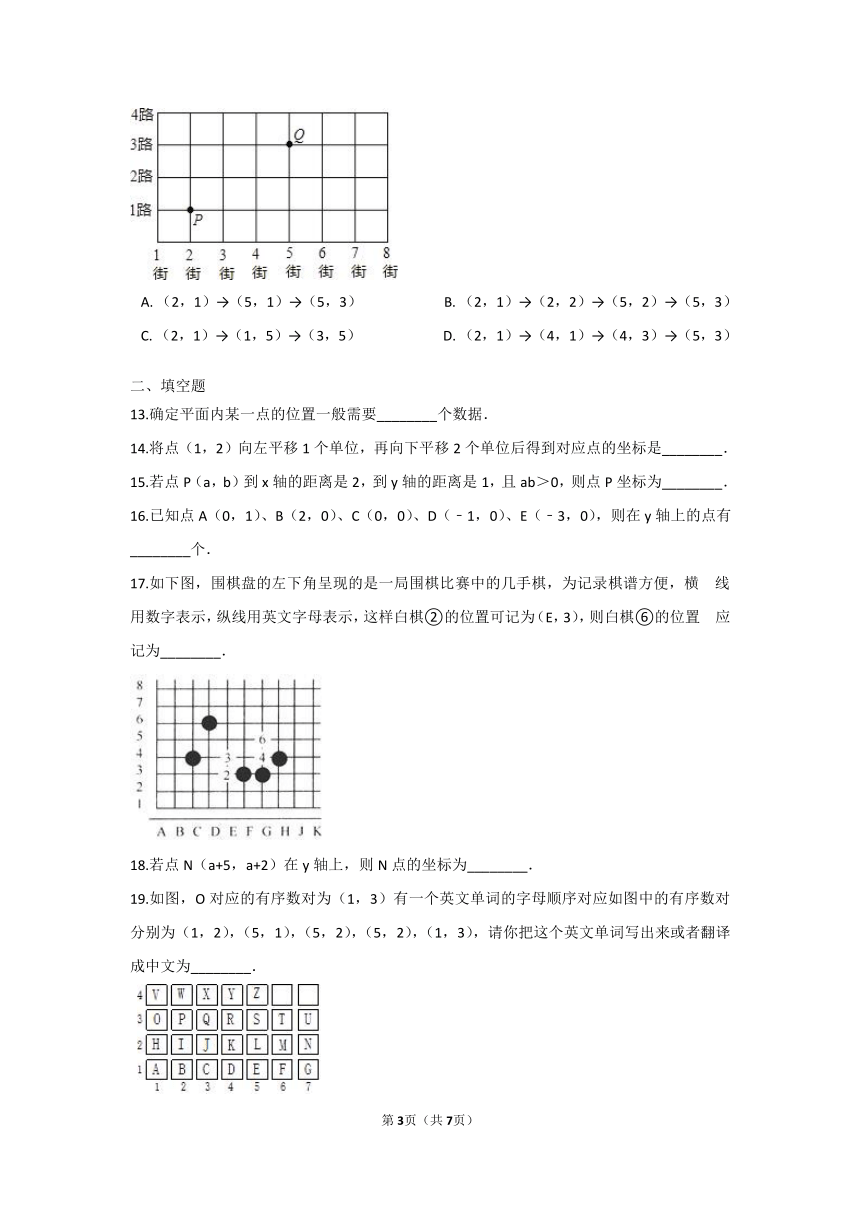
12.如图是某城市的部分街道平面图的示意图,某人从P地出发到Q地,他的路径表示错误的是( )
A.?(2,1)→(5,1)→(5,3)????????????????????????B.?(2,1)→(2,2)→(5,2)→(5,3) C.?(2,1)→(1,5)→(3,5)????????????????????????D.?(2,1)→(4,1)→(4,3)→(5,3)
二、填空题
13.确定平面内某一点的位置一般需要________个数据.
14.将点(1,2)向左平移1个单位,再向下平移2个单位后得到对应点的坐标是________.
15.若点P(a,b)到x轴的距离是2,到y轴的距离是1,且ab>0,则点P坐标为________.
16.已知点A(0,1)、B(2,0)、C(0,0)、D(﹣1,0)、E(﹣3,0),则在y轴上的点有________个.
17.如下图,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横 线用数字表示,纵线用英文字母表示,这样白棋②的位置可记为(E,3),则白棋⑥的位置 应记为________.
18.若点N(a+5,a+2)在y轴上,则N点的坐标为________.
19.如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为________.
20.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1 , 半圆O2 , 半圆O3 , …,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 个单位长度,则第101秒时,点P的坐标是________.
21.课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用(0,0)表示,小颖的位置用(2,1)表示,那么小浩的位置可以表示成________.
22.点A(m+3,m+1)在x轴上,则点A坐标为________.
三、解答题
23.在平面直角坐标系中已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,求点P的坐标.
24.在雷达探测区域,可以建立平面直角坐标系表示位置.在某次行动中,当我两 架飞机在A(-1,2)与B(3,2)位置时,可疑飞机在(-1,-3)位置,你能找到这个直角坐标系的横、纵坐标 的位置吗?把它们表示出来并确定可疑飞机的位置,说说你的做法.
25.在平面直角坐标系内,已知A(2x,3x+1).
(1)点A在x轴下方,在y轴的左侧,且到两坐标轴的距离相等,求x的值;
(2)若x=1,点B在x轴上,且S△OAB=6,求点B的坐标.
26.如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
27.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”. 例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(﹣1,6)的“2属派生点”P′的坐标为________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
参考答案
一、选择题
B B B A C A D C D A D C
二、填空题
13. 2
14. (0,0)
15. (1,2)或(﹣1,﹣2)
16. 2
17. (G,5)
18. (0,﹣3)
19. HELLO
20. (101,1)
21. (4,3)
22. (2,0)
三、解答题
23. 解:∵S△PAB= AP?2=5, 解得AP=5, 若点P在点A的左边,则OP=5﹣1=4, 此时,点P的坐标为(﹣4,0), 若点P在点A的右边,则OP=1+5=6, 此时,点P的坐标为(6,0).
24. 解:能.如下图,先把AB四等分,然后过靠近A点的分点M作AB的垂线即为y轴,以AM为单位长度沿y轴向下2个单位即为O点,过点O作x轴垂直于y轴,然后描出敌机位置为点N.
25. (1)解:∵点A在x轴下方,在y轴的左侧, ∴点A在第三象限, ∵点A到两坐标轴的距离相等, ∴2x=3x+1,解得:x=﹣1 (2)解:若x=1,则A(2,4), 设B(a,0), ∵S△OAB=6, ∴ ×4×|a|=6, 解得:a=±3, ∴点B的坐标为(3,0)或(﹣3,0)
26. (1)解:∵B(8,0),C(8,6), ∴BC=6, ∴S△ABC= ×6×8=24; (2)解:∵A(0,4)(8,0), ∴OA=4,OB=8, ∴S四边形ABOP=S△AOB+S△AOP = ×4×8+ ×4(﹣m)=16﹣2m, 又∵S四边形ABOP=2S△ABC=48, ∴16﹣2m=48, 解得:m=﹣16, ∴P(﹣16,1).
27. (1)(11,4) (2)(0,2) (3)解:∵点P在x轴的正半轴上, ∴b=0,a>0. ∴点P的坐标为(a,0),点P′的坐标为(a,ka) ∴线段PP′的长为P′到x轴距离为|ka|. ∵P在x轴正半轴,线段OP的长为a, ∴|ka|=2a,即|k|=2, ∴k=±2.
一、选择题
1.在平面直角坐标系中,点A(-4,0)在( )
A.?x轴正半轴上;?????????????????B.?x轴负半轴上;?????????????????
C.?y轴正半轴上;?????????????????D.?y轴负半轴上
2.点P(m+3,m+1)在直角坐标系的x轴上,则P点的坐标为(? )
A.?(0,﹣2)????????????????????????B.?(2,0)????????????????????????C.?(0,2)????????????????????????D.?(0,﹣4)
3.已知y轴上的点P到原点的距离为5,则点P的坐标为(?? )
A.?(5,0)???????????? B.?(0,5)或(0,﹣5)?????????
???C.?(0,5)????????????D.?(5,0)或(﹣5,0)
4.如图是丁丁画的一张脸的示意图,如果用(0,2)表示靠左边的眼睛,用(2,2)表示靠右边的眼睛,那么嘴的位置可以表示成( )
A.?(1,0)???????????????????????B.?(﹣1,0)???????????????????????C.?(﹣1,1)???????????????????????D.?(1,﹣1)
5.如下图所示,图中是沈阳市地图简图的一部分,图中“故宫”、“鼓楼”所在的区域分别是(??? )
D
E
F
6
鼓楼
大北门
7
故宫
8
大南门
东华门
A.D7,E6 B.D6,E7 C.E7,D6 D.E6,D7
6.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是(????? )
A.?(7,0)???????????????????????????B.?(0,7)???????????????????????????C.?(7,7)???????????????????????????D.?(6,0)
7.根据下列表述,能确定具体位置的是(? ??)
A.?某电影院2排???????????????????B.?大桥南路?????????????????
??C.?北偏东30°?????????????????? ?D.?东经108°,北纬43°
8.中国象棋具有悠久的历史,战国时期,就有了关于象棋的正式记载,如图是中国象棋棋局的一部分,如果用(2,﹣1)表示“炮”的位置,那么“将”的位置应表示为(?? )
A.?(﹣2,3)??????????????????????B.?(0,﹣5)??????????????????????C.?(﹣3,1)??????????????????????D.?(﹣4,2)
9.已知点P位于y轴的右侧,距y轴5个单位长度,位于x轴上方,距x轴6个单位长度,则点P的坐标是( )
A.?(﹣5,6)????????????????????????B.?(6,5)????????????????????????C.?(﹣6,5)????????????????????????D.?(5,6)
10.若点P在第二象限内,且到x轴的距离是5,到y轴的距离是7,则点P的坐标是(?? )
A.?(﹣7,5)??????????????????????B.?(7,﹣5)??????????????????????C.?(﹣5,7)??????????????????????D.?(5,﹣7)
11.点M到x轴的距离为3,到y的距离为4,则点M的坐标为(????)
A.?(3,4)??????????????????????????????????????????????????B.?(4,3) C.?(4,3),(-4,3)????????????????????????????D.?(4,3),(-4,3),(-4,-3)或(4,-3)
12.如图是某城市的部分街道平面图的示意图,某人从P地出发到Q地,他的路径表示错误的是( )
A.?(2,1)→(5,1)→(5,3)????????????????????????B.?(2,1)→(2,2)→(5,2)→(5,3) C.?(2,1)→(1,5)→(3,5)????????????????????????D.?(2,1)→(4,1)→(4,3)→(5,3)
二、填空题
13.确定平面内某一点的位置一般需要________个数据.
14.将点(1,2)向左平移1个单位,再向下平移2个单位后得到对应点的坐标是________.
15.若点P(a,b)到x轴的距离是2,到y轴的距离是1,且ab>0,则点P坐标为________.
16.已知点A(0,1)、B(2,0)、C(0,0)、D(﹣1,0)、E(﹣3,0),则在y轴上的点有________个.
17.如下图,围棋盘的左下角呈现的是一局围棋比赛中的几手棋,为记录棋谱方便,横 线用数字表示,纵线用英文字母表示,这样白棋②的位置可记为(E,3),则白棋⑥的位置 应记为________.
18.若点N(a+5,a+2)在y轴上,则N点的坐标为________.
19.如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为________.
20.如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1 , 半圆O2 , 半圆O3 , …,组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 个单位长度,则第101秒时,点P的坐标是________.
21.课间操时,小颖、小浩的位置如图所示,小明对小浩说,如果我的位置用(0,0)表示,小颖的位置用(2,1)表示,那么小浩的位置可以表示成________.
22.点A(m+3,m+1)在x轴上,则点A坐标为________.
三、解答题
23.在平面直角坐标系中已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,求点P的坐标.
24.在雷达探测区域,可以建立平面直角坐标系表示位置.在某次行动中,当我两 架飞机在A(-1,2)与B(3,2)位置时,可疑飞机在(-1,-3)位置,你能找到这个直角坐标系的横、纵坐标 的位置吗?把它们表示出来并确定可疑飞机的位置,说说你的做法.
25.在平面直角坐标系内,已知A(2x,3x+1).
(1)点A在x轴下方,在y轴的左侧,且到两坐标轴的距离相等,求x的值;
(2)若x=1,点B在x轴上,且S△OAB=6,求点B的坐标.
26.如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.
27.对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”. 例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(﹣1,6)的“2属派生点”P′的坐标为________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
参考答案
一、选择题
B B B A C A D C D A D C
二、填空题
13. 2
14. (0,0)
15. (1,2)或(﹣1,﹣2)
16. 2
17. (G,5)
18. (0,﹣3)
19. HELLO
20. (101,1)
21. (4,3)
22. (2,0)
三、解答题
23. 解:∵S△PAB= AP?2=5, 解得AP=5, 若点P在点A的左边,则OP=5﹣1=4, 此时,点P的坐标为(﹣4,0), 若点P在点A的右边,则OP=1+5=6, 此时,点P的坐标为(6,0).
24. 解:能.如下图,先把AB四等分,然后过靠近A点的分点M作AB的垂线即为y轴,以AM为单位长度沿y轴向下2个单位即为O点,过点O作x轴垂直于y轴,然后描出敌机位置为点N.
25. (1)解:∵点A在x轴下方,在y轴的左侧, ∴点A在第三象限, ∵点A到两坐标轴的距离相等, ∴2x=3x+1,解得:x=﹣1 (2)解:若x=1,则A(2,4), 设B(a,0), ∵S△OAB=6, ∴ ×4×|a|=6, 解得:a=±3, ∴点B的坐标为(3,0)或(﹣3,0)
26. (1)解:∵B(8,0),C(8,6), ∴BC=6, ∴S△ABC= ×6×8=24; (2)解:∵A(0,4)(8,0), ∴OA=4,OB=8, ∴S四边形ABOP=S△AOB+S△AOP = ×4×8+ ×4(﹣m)=16﹣2m, 又∵S四边形ABOP=2S△ABC=48, ∴16﹣2m=48, 解得:m=﹣16, ∴P(﹣16,1).
27. (1)(11,4) (2)(0,2) (3)解:∵点P在x轴的正半轴上, ∴b=0,a>0. ∴点P的坐标为(a,0),点P′的坐标为(a,ka) ∴线段PP′的长为P′到x轴距离为|ka|. ∵P在x轴正半轴,线段OP的长为a, ∴|ka|=2a,即|k|=2, ∴k=±2.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
