北师大版八年级下册数学 2.5一元一次不等式与一次函数导学案(含答案)
文档属性
| 名称 | 北师大版八年级下册数学 2.5一元一次不等式与一次函数导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 09:19:23 | ||
图片预览



文档简介
导学案:一元一次不等式与一次函数的关系
【学习目标】
1、一元一次不等式与一次函数的关系。
2、会根据题意列出函数关系式,画出函数图象,并利用不等关系进行比较。
3、通过一元一次不等式与一次函数的图象之间的结合,培养数形结合意识。
【学习重点】
了解一元一次不等式与一次函数之间的关系。
【学习难点】
根据题意列函数关系式,并能把函数关系式与一元一次不等式联系起来作答。
【学习过程】
一、复习导学
前面我们学习过一次函数、一元一次方程与一元一次不等式,我们知道一元一次方程的解就是一次函数图象与x轴交点的横坐标,也就是说:
“一元一次方程ax+b=0”与“求当x为何值时,y=ax+b的值为0”是同一问题,
那么一元一次不等式与一次函数之间有怎样的关系呢?
如:下面两个问题是同一问题吗?
(1)解不等式:2x-4<0
(2)当x为何值时,函数y=2x-4的值小于0?
今天我们就来探究类似这样的问题?
二、自主探究、合作交流
1.探讨一下一元一次不等式与一次函数的图象之间的关系:
还记得一次函数吗?请举例给出它的一般形式.
如y=2x-5为一次函数.
在一次函数y=2x-5中,
当y=0时,有方程2x-5=0;
当y>0时,有不等式2x-5>0;
当y<0时,有不等式2x-5<0.
由此可见:_________________________________________________________________
___________________________________________________________________________.
2.做一做:
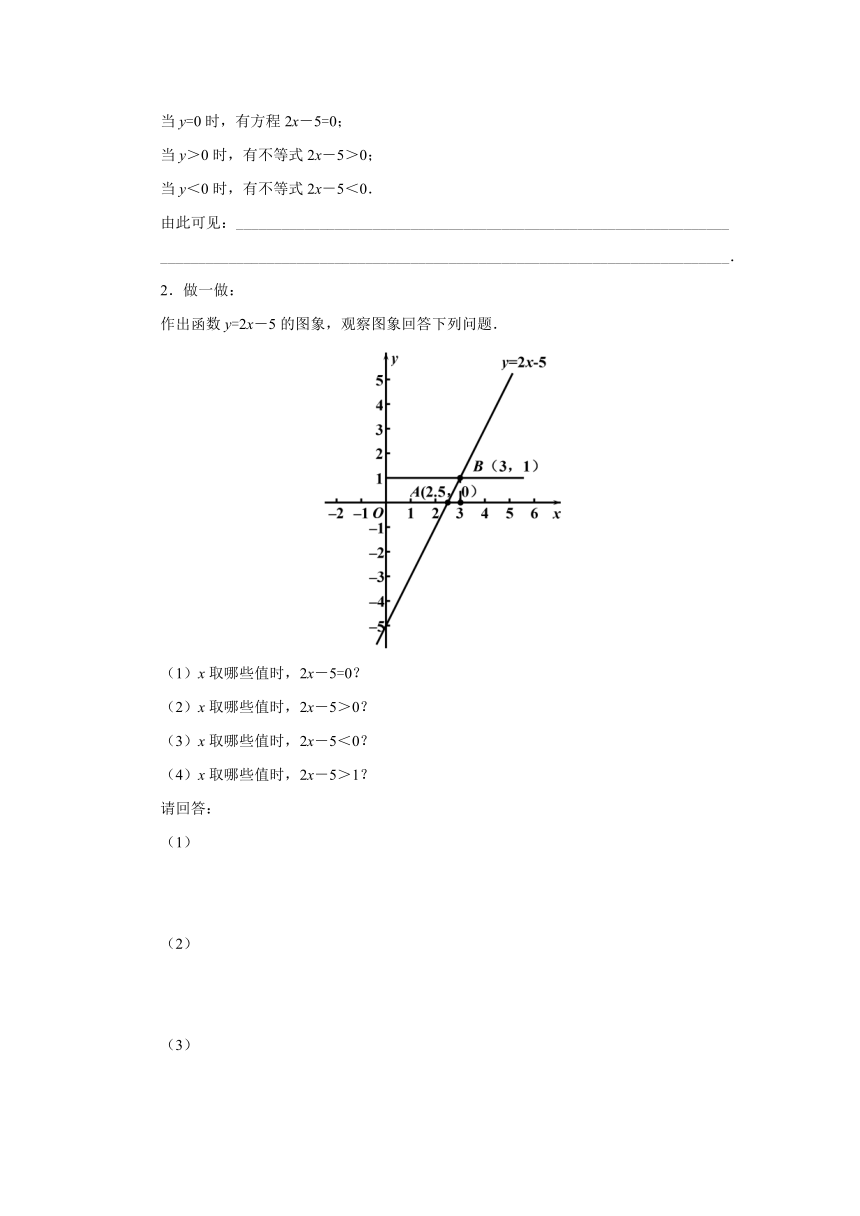
作出函数y=2x-5的图象,观察图象回答下列问题.
(1)x取哪些值时,2x-5=0?
(2)x取哪些值时,2x-5>0?
(3)x取哪些值时,2x-5<0?
(4)x取哪些值时,2x-5>1?
请回答:
(1)
(2)
(3)
(4)
3.试一试
如果y=-2x-5,那么当x取何值时,y>0?
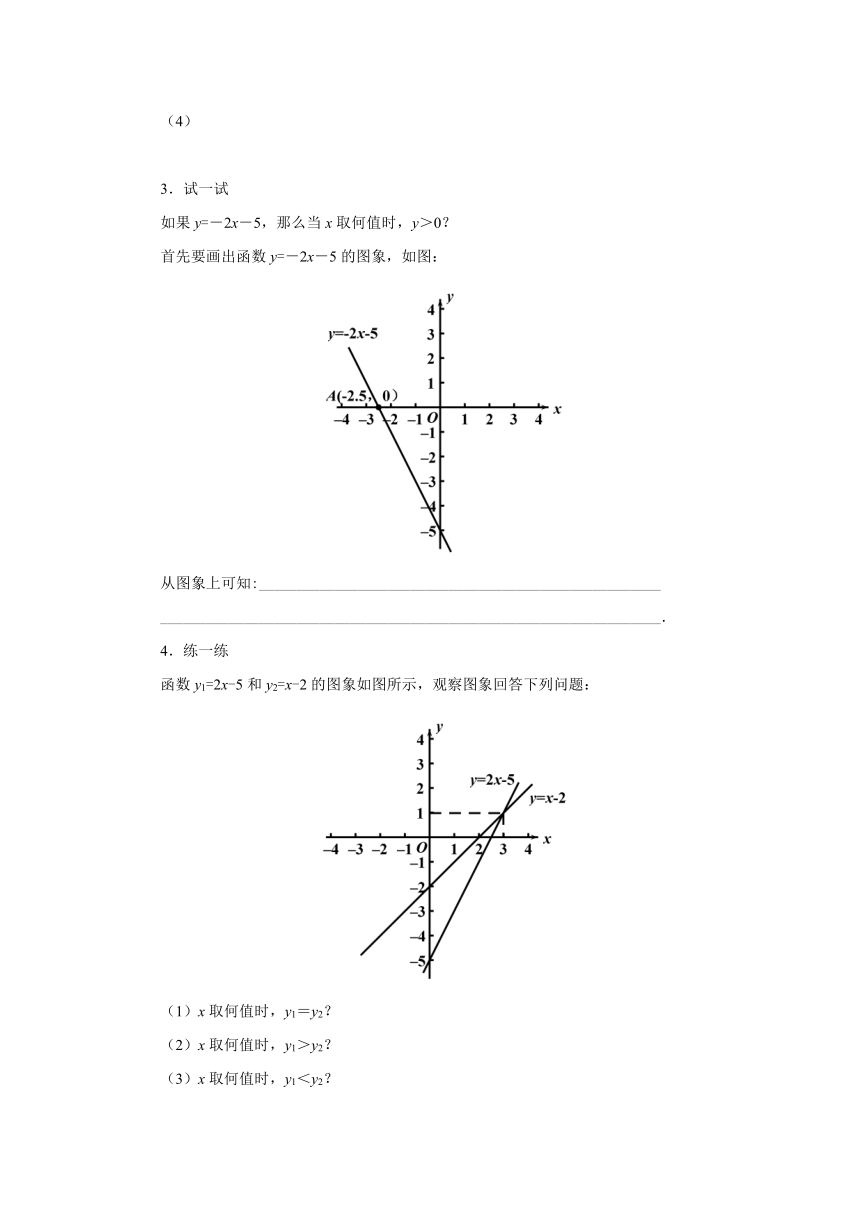
首先要画出函数y=-2x-5的图象,如图:
从图象上可知:_____________________________________________________
__________________________________________________________________.
4.练一练
函数y1=2x-5和y2=x-2的图象如图所示,观察图象回答下列问题:
(1)x取何值时,y1=y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1<y2?
从图象上看:
总结一次函数与一元一次不等式的关系:
从数的角度看
从形的角度看
三、应用新知、拓展提升
(一)基础演练
1.已知函数y=3x+8,当x________________________时,函数的值等于0.当x_________________________时,函数的值大于0.当x__________________________________时,函数的值不大于2.
2.如图,直线l1,l2交于一点P,若y1≥y2,则( )
A.x≥3 B.x≤3 C.2≤x≤ 3 D.x≤4
(二)典例示范
例1 .作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题:
(1)x取何值时,2x-4>0?
(2)x取何值时,-2x+8>0?
(3)x取何值时,2x-4>0与-2x+8>0同时成立?
(4)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?并写出过程.
例2.一次函数y=-3x+12中,x为何值时:
(1)当x取何值时,y>0;
(2)当x取何值时,y=0;
(3)当x取何值时,y<0 .
(三)拓展提升
例3.已知y1=-x+3,y2=3x-4,当x取何值时,y1>y2?你是怎样做的?
四、课堂小结
(
转化
)1.转化思想:
__________问题 ___________问题
2.解函数问题的方法:
图象法:_________________________________.
3.一次函数与一元一次不等式的关系:
从数的角度看
从形的角度看
五、课堂检测
1.已知y1=x-5,y2=2x+1.当y1>y2时,x的取值范围是( )
A.x>5 B.x< C.x<-6 D.x>-6
2.已知一次函数的图象如图所示,当x<1时,y的取值范围是( )
(
-
4
y
O
2
x
)
A.-2<y<0 B.-4<y<0 C.y<-2 D.y<-4
3.若一次函数y=(m-1)x-m+4的图象与y轴的交点在x轴的上方,则m的取值范围是________.
4.已知,试确定取何值时不小于?
5.在同一坐标系中画出一次函数y1=-x+1与y2=2x-2的图象,并根据图象回答下列问题:
(1)写出直线y1=-x+1与y2=2x-2的交点P的坐标.
(2)直接写出:当x取何值时y1>y2;y1<y2
参考答案:
一、复习导学
二、自主探究、合作交流
1.探讨一下一元一次不等式与一次函数的图象之间的关系:
一次函数与一元一次方程、一元一次不等式之间有密切关系,当函数值等于0时即为方程,当函数值大于或小于0时即为不等式.
2.做一做:
(1)当y=0时,2x-5=0,
∴x=,
∴当x=时,2x-5=0.
(2)要找2x-5>0的x的值,也就是函数值y大于0时所对应的x的值,从图象上可知,y>0时,图象在x轴上方,图象上任一点所对应的x值都满足条件.当x>时,由y=2x-5可知y>0.因此当x>时,2x-5>0.
(3)同理可知,当x<时,有2x-5<0;
(4)要使2x-5>1,也就是y=2x-5中的y大于1,那么过纵坐标为1的点作一条直线平行于x轴,这条直线与y=2x-5相交于一点B(3,1),则当x>3时,有2x-5>1.
3.试一试
从图象上可知,图象在x轴上方时,图象上每一点所对应的y的值都大于0,而每一个y的值所对应的x的值都在A点的左侧,即为小于-2.5的数,由-2x-5=0,得x=-2.5,所以当x取小于-2.5的值时,y>0.
4.练一练
从图象上看,
(1)y1=y2时,两个一次函数的图象交于一点,此点的横坐标就是方程2x-5=x-2的解;
(2)一次函数y1=2x-5的图象在y2=x-2的图象上方的部分对应点的横坐标就是不等式2x-5>x-2的解;
(3)一次函数y1=2x-5的图象在y2=x-2的图象下方的部分对应点的横坐标就是不等式2x-5<x-2的解.
总结一次函数与一元一次不等式的关系:
从数的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求函数y=ax+b的函数值大于0(或小于0)时x的取值范围.
从形的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求直线y=ax+b在x轴上方或下方时自变量的取值范围
三、应用新知、拓展提升
(一)基础演练
1.= ,﹥ ,﹤﹣2. 2.B
(二)典例示范
例1 .
分析:要使2x-4>0成立,就是y1=2x-4的图象在x轴上方的所有点的横坐标的集合,同理使-2x+8>0成立的x,即为函数y2=-2x+8的图象在x轴上方的所有点的横坐标的集合,要使它们同时成立,即求这两个集合中公共的x,根据函数图象与x轴交点的坐标可求出三角形的底边长,由两函数的交点坐标可求出底边上的高,从而求出三角形的面积.
解:
(1)当x>2时,2x-4>0;
(2)当x<4时,-2x+8>0;
(3)当2<x<4时,2x-4>0与-2x+8>0同时成立;
(4)由2x-4=0,得x=2.
由-2x+8=0,得x=4.
所以AB=4-2=2.
由
得交点C(3,2).
所以△ABC中AB边上的高为2.
所以S=×2×2=2.
例2.
解:(1)当y>0时,则有-3x+12>0,
-3x>-12, x<4
(2)当y=0时,则有-3x+12=0,
-3x=-12, x=4
(3)当y<0时,则有-3x+12<0,
-3x<-12, x>4
(三)拓展提升
例3.
解:如图所示:
当x取小于的值时,有y1>y2.
四、课堂小结
(
转化
)1.转化思想:
一次不等式问题 一次函数问题
2.解函数问题的方法:
图象法:画出函数图象解决函数和不等式问题.
3.一次函数与一元一次不等式的关系:
从数的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求函数y=ax+b的函数值大于0(或小于0)时x的取值范围.
从形的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求直线y=ax+b在x轴上方或下方时自变量的取值范围
五、课堂检测
1.C. 2.C. 3.m<4且m≠1.
4.当时不小于.
5.图象略.(1)P(1,0); (2)当x<1时y1>y2,当x>1时y1<y2.
【学习目标】
1、一元一次不等式与一次函数的关系。
2、会根据题意列出函数关系式,画出函数图象,并利用不等关系进行比较。
3、通过一元一次不等式与一次函数的图象之间的结合,培养数形结合意识。
【学习重点】
了解一元一次不等式与一次函数之间的关系。
【学习难点】
根据题意列函数关系式,并能把函数关系式与一元一次不等式联系起来作答。
【学习过程】
一、复习导学
前面我们学习过一次函数、一元一次方程与一元一次不等式,我们知道一元一次方程的解就是一次函数图象与x轴交点的横坐标,也就是说:
“一元一次方程ax+b=0”与“求当x为何值时,y=ax+b的值为0”是同一问题,
那么一元一次不等式与一次函数之间有怎样的关系呢?
如:下面两个问题是同一问题吗?
(1)解不等式:2x-4<0
(2)当x为何值时,函数y=2x-4的值小于0?
今天我们就来探究类似这样的问题?
二、自主探究、合作交流
1.探讨一下一元一次不等式与一次函数的图象之间的关系:
还记得一次函数吗?请举例给出它的一般形式.
如y=2x-5为一次函数.
在一次函数y=2x-5中,
当y=0时,有方程2x-5=0;
当y>0时,有不等式2x-5>0;
当y<0时,有不等式2x-5<0.
由此可见:_________________________________________________________________
___________________________________________________________________________.
2.做一做:
作出函数y=2x-5的图象,观察图象回答下列问题.
(1)x取哪些值时,2x-5=0?
(2)x取哪些值时,2x-5>0?
(3)x取哪些值时,2x-5<0?
(4)x取哪些值时,2x-5>1?
请回答:
(1)
(2)
(3)
(4)
3.试一试
如果y=-2x-5,那么当x取何值时,y>0?
首先要画出函数y=-2x-5的图象,如图:
从图象上可知:_____________________________________________________
__________________________________________________________________.
4.练一练
函数y1=2x-5和y2=x-2的图象如图所示,观察图象回答下列问题:
(1)x取何值时,y1=y2?
(2)x取何值时,y1>y2?
(3)x取何值时,y1<y2?
从图象上看:
总结一次函数与一元一次不等式的关系:
从数的角度看
从形的角度看
三、应用新知、拓展提升
(一)基础演练
1.已知函数y=3x+8,当x________________________时,函数的值等于0.当x_________________________时,函数的值大于0.当x__________________________________时,函数的值不大于2.
2.如图,直线l1,l2交于一点P,若y1≥y2,则( )
A.x≥3 B.x≤3 C.2≤x≤ 3 D.x≤4
(二)典例示范
例1 .作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题:
(1)x取何值时,2x-4>0?
(2)x取何值时,-2x+8>0?
(3)x取何值时,2x-4>0与-2x+8>0同时成立?
(4)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?并写出过程.
例2.一次函数y=-3x+12中,x为何值时:
(1)当x取何值时,y>0;
(2)当x取何值时,y=0;
(3)当x取何值时,y<0 .
(三)拓展提升
例3.已知y1=-x+3,y2=3x-4,当x取何值时,y1>y2?你是怎样做的?
四、课堂小结
(
转化
)1.转化思想:
__________问题 ___________问题
2.解函数问题的方法:
图象法:_________________________________.
3.一次函数与一元一次不等式的关系:
从数的角度看
从形的角度看
五、课堂检测
1.已知y1=x-5,y2=2x+1.当y1>y2时,x的取值范围是( )
A.x>5 B.x< C.x<-6 D.x>-6
2.已知一次函数的图象如图所示,当x<1时,y的取值范围是( )
(
-
4
y
O
2
x
)
A.-2<y<0 B.-4<y<0 C.y<-2 D.y<-4
3.若一次函数y=(m-1)x-m+4的图象与y轴的交点在x轴的上方,则m的取值范围是________.
4.已知,试确定取何值时不小于?
5.在同一坐标系中画出一次函数y1=-x+1与y2=2x-2的图象,并根据图象回答下列问题:
(1)写出直线y1=-x+1与y2=2x-2的交点P的坐标.
(2)直接写出:当x取何值时y1>y2;y1<y2
参考答案:
一、复习导学
二、自主探究、合作交流
1.探讨一下一元一次不等式与一次函数的图象之间的关系:
一次函数与一元一次方程、一元一次不等式之间有密切关系,当函数值等于0时即为方程,当函数值大于或小于0时即为不等式.
2.做一做:
(1)当y=0时,2x-5=0,
∴x=,
∴当x=时,2x-5=0.
(2)要找2x-5>0的x的值,也就是函数值y大于0时所对应的x的值,从图象上可知,y>0时,图象在x轴上方,图象上任一点所对应的x值都满足条件.当x>时,由y=2x-5可知y>0.因此当x>时,2x-5>0.
(3)同理可知,当x<时,有2x-5<0;
(4)要使2x-5>1,也就是y=2x-5中的y大于1,那么过纵坐标为1的点作一条直线平行于x轴,这条直线与y=2x-5相交于一点B(3,1),则当x>3时,有2x-5>1.
3.试一试
从图象上可知,图象在x轴上方时,图象上每一点所对应的y的值都大于0,而每一个y的值所对应的x的值都在A点的左侧,即为小于-2.5的数,由-2x-5=0,得x=-2.5,所以当x取小于-2.5的值时,y>0.
4.练一练
从图象上看,
(1)y1=y2时,两个一次函数的图象交于一点,此点的横坐标就是方程2x-5=x-2的解;
(2)一次函数y1=2x-5的图象在y2=x-2的图象上方的部分对应点的横坐标就是不等式2x-5>x-2的解;
(3)一次函数y1=2x-5的图象在y2=x-2的图象下方的部分对应点的横坐标就是不等式2x-5<x-2的解.
总结一次函数与一元一次不等式的关系:
从数的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求函数y=ax+b的函数值大于0(或小于0)时x的取值范围.
从形的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求直线y=ax+b在x轴上方或下方时自变量的取值范围
三、应用新知、拓展提升
(一)基础演练
1.= ,﹥ ,﹤﹣2. 2.B
(二)典例示范
例1 .
分析:要使2x-4>0成立,就是y1=2x-4的图象在x轴上方的所有点的横坐标的集合,同理使-2x+8>0成立的x,即为函数y2=-2x+8的图象在x轴上方的所有点的横坐标的集合,要使它们同时成立,即求这两个集合中公共的x,根据函数图象与x轴交点的坐标可求出三角形的底边长,由两函数的交点坐标可求出底边上的高,从而求出三角形的面积.
解:
(1)当x>2时,2x-4>0;
(2)当x<4时,-2x+8>0;
(3)当2<x<4时,2x-4>0与-2x+8>0同时成立;
(4)由2x-4=0,得x=2.
由-2x+8=0,得x=4.
所以AB=4-2=2.
由
得交点C(3,2).
所以△ABC中AB边上的高为2.
所以S=×2×2=2.
例2.
解:(1)当y>0时,则有-3x+12>0,
-3x>-12, x<4
(2)当y=0时,则有-3x+12=0,
-3x=-12, x=4
(3)当y<0时,则有-3x+12<0,
-3x<-12, x>4
(三)拓展提升
例3.
解:如图所示:
当x取小于的值时,有y1>y2.
四、课堂小结
(
转化
)1.转化思想:
一次不等式问题 一次函数问题
2.解函数问题的方法:
图象法:画出函数图象解决函数和不等式问题.
3.一次函数与一元一次不等式的关系:
从数的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求函数y=ax+b的函数值大于0(或小于0)时x的取值范围.
从形的角度看
求ax+b>0(或<0)(a,b是常数,a≠0)的解集就是求直线y=ax+b在x轴上方或下方时自变量的取值范围
五、课堂检测
1.C. 2.C. 3.m<4且m≠1.
4.当时不小于.
5.图象略.(1)P(1,0); (2)当x<1时y1>y2,当x>1时y1<y2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
