人教版七年级数学下册5.2.2平行线的判定课件 (20ppt)
文档属性
| 名称 | 人教版七年级数学下册5.2.2平行线的判定课件 (20ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 863.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第五章 相交线与平行线
第6课时 平行线的判定
学习目标
1
2
3
掌握平行线判定的方法,并且会学以致用
利用所学方法进行简单的几何证明且会用数学几何语言表达
体会数学的“转化”思想
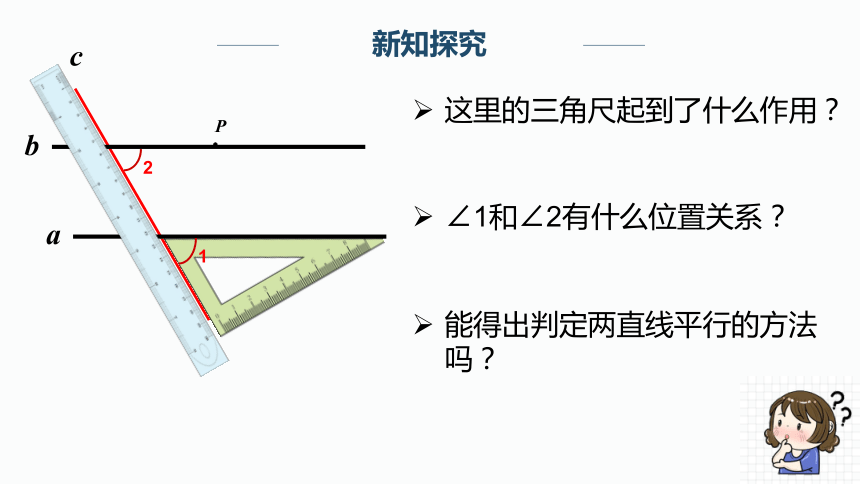
新知探究
1
a
b
.
P
2
这里的三角尺起到了什么作用?
∠1和∠2有什么位置关系?
能得出判定两直线平行的方法吗?
c
新知探究
1
a
b
.
P
2
判定方法1:
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
c
几何语言
∵∠1=∠2
∴a∥b
简单说成,同位角相等,两直线平行
学以致用
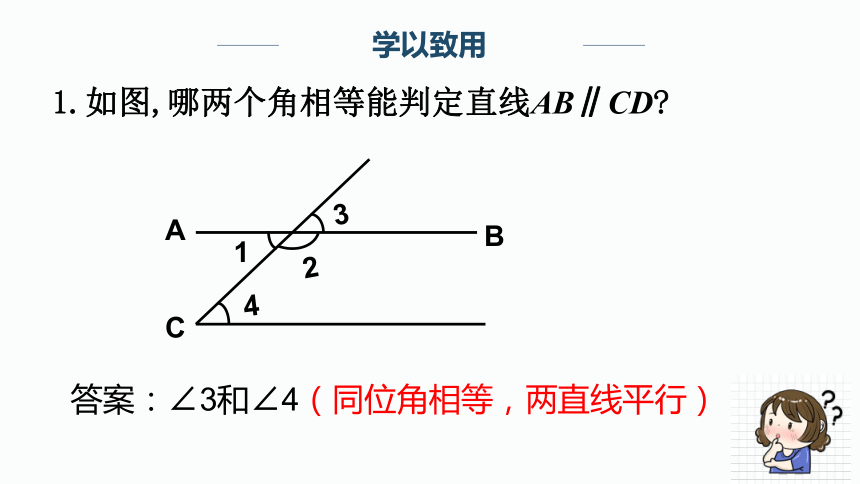
1.如图,哪两个角相等能判定直线AB∥CD?
B
1
4
3
2
A
C
答案:∠3和∠4(同位角相等,两直线平行)
学以致用
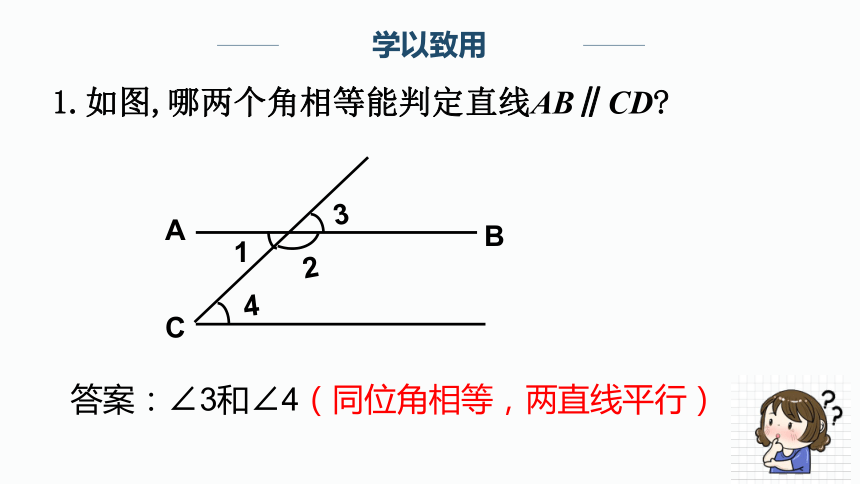
1.如图,哪两个角相等能判定直线AB∥CD?
B
1
4
3
2
A
C
答案:∠3和∠4(同位角相等,两直线平行)
学以致用
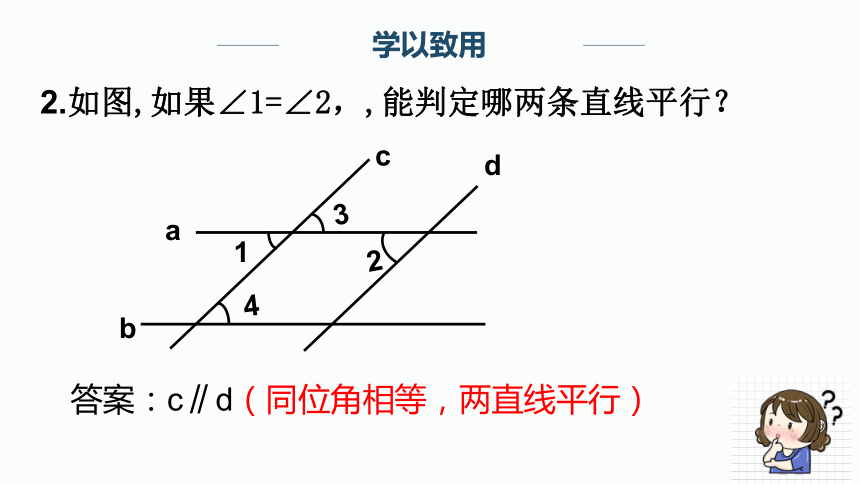
2.如图,如果∠1=∠2,,能判定哪两条直线平行?
1
4
3
2
a
b
答案:c∥d(同位角相等,两直线平行)
c
d
探究新知
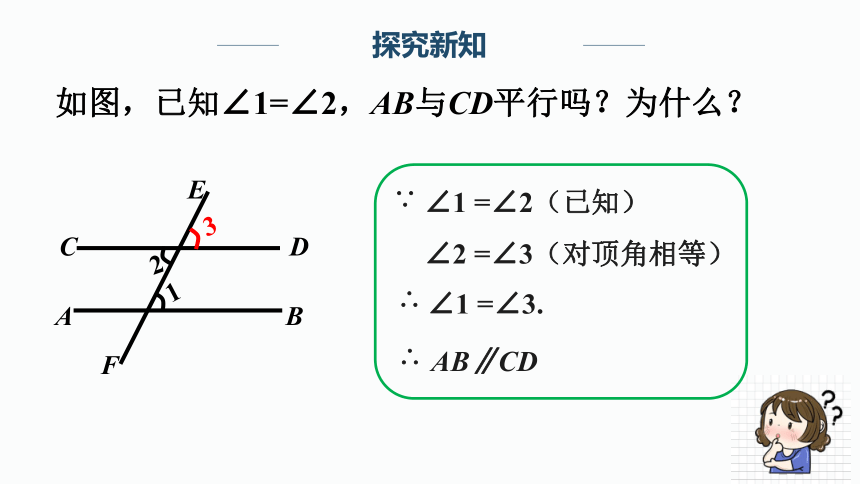
如图,已知∠1=∠2,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
3
?
∠1 =∠2(已知)
∠2 =∠3(对顶角相等)
?
∠1 =∠3.
?
AB∥CD
判定方法2
A
B
C
D
E
F
1
2
3
判定方法2
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
几何语言
∵∠1=∠2
∴a∥b
简单说成:内错角相等,两直线平行
学以致用
1.如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
解:
∵∠1=∠2,∠1=∠3
∴∠2=∠3
∴AB∥CD
新知探究
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
1
2
3
?
∠1 +∠2=180°(已知)
∠2 +∠3=180°(邻补角互补)
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(内错角相等,两直线平行)
判定方法3
判定方法3
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行
A
B
C
D
E
F
1
2
几何语言
∵∠1+∠2=180°
∴AB∥BC
简单说成:同旁内角互补,两直线平行
学以致用
D
C
B
A
答:AB//CD,AD//BC
∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
如图:?B= ? D=45°, ? C=135°,问图中有哪些直线平行?
课堂总结
【判定方法1】
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
【判定方法2】
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
【判定方法3】
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行
课堂练习
C
课堂练习
A
课堂练习
D
课堂练习
A
课堂练习
D
课堂练习
D
第五章 相交线与平行线
第6课时 平行线的判定
学习目标
1
2
3
掌握平行线判定的方法,并且会学以致用
利用所学方法进行简单的几何证明且会用数学几何语言表达
体会数学的“转化”思想
新知探究
1
a
b
.
P
2
这里的三角尺起到了什么作用?
∠1和∠2有什么位置关系?
能得出判定两直线平行的方法吗?
c
新知探究
1
a
b
.
P
2
判定方法1:
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
c
几何语言
∵∠1=∠2
∴a∥b
简单说成,同位角相等,两直线平行
学以致用
1.如图,哪两个角相等能判定直线AB∥CD?
B
1
4
3
2
A
C
答案:∠3和∠4(同位角相等,两直线平行)
学以致用
1.如图,哪两个角相等能判定直线AB∥CD?
B
1
4
3
2
A
C
答案:∠3和∠4(同位角相等,两直线平行)
学以致用
2.如图,如果∠1=∠2,,能判定哪两条直线平行?
1
4
3
2
a
b
答案:c∥d(同位角相等,两直线平行)
c
d
探究新知
如图,已知∠1=∠2,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
3
?
∠1 =∠2(已知)
∠2 =∠3(对顶角相等)
?
∠1 =∠3.
?
AB∥CD
判定方法2
A
B
C
D
E
F
1
2
3
判定方法2
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
几何语言
∵∠1=∠2
∴a∥b
简单说成:内错角相等,两直线平行
学以致用
1.如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
解:
∵∠1=∠2,∠1=∠3
∴∠2=∠3
∴AB∥CD
新知探究
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
1
2
3
?
∠1 +∠2=180°(已知)
∠2 +∠3=180°(邻补角互补)
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(内错角相等,两直线平行)
判定方法3
判定方法3
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行
A
B
C
D
E
F
1
2
几何语言
∵∠1+∠2=180°
∴AB∥BC
简单说成:同旁内角互补,两直线平行
学以致用
D
C
B
A
答:AB//CD,AD//BC
∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
如图:?B= ? D=45°, ? C=135°,问图中有哪些直线平行?
课堂总结
【判定方法1】
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
【判定方法2】
两条直线被第三条直线所截 ,如果内错角相等, 那么这两条直线平行.
【判定方法3】
两条直线被第三条直线所截 ,如果同旁内角互补, 那么这两条直线平行
课堂练习
C
课堂练习
A
课堂练习
D
课堂练习
A
课堂练习
D
课堂练习
D
