高中数学苏教版必修二第二章第一节 直线的斜率课件(共25张PPT)
文档属性
| 名称 | 高中数学苏教版必修二第二章第一节 直线的斜率课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 20:57:26 | ||
图片预览








文档简介
(共25张PPT)
江苏省宝应中学
平面解析几何,就是通过引进直角坐标系,建立点与坐标、曲线与方程之间的对应关系,将几何问题转化为代数问题,从而用代数方法研究几何问题.充分体现了数形结合的数学思想。
直 线 的 斜 率
问题1:
(1)一块长方形的钢板ABCD,你能
画出它的对角线BD吗?
(2)
你能总结一下,如何才能确定一条直线吗?
问题2:通过建立直角坐标系,点可以用坐标来刻画,那么,直线的倾斜程度如何用一个代数的量来刻画呢?
.
.
.
x
y
o
y
x
o
结论:坡度越大,楼梯越陡.
0.8m
1m
0.4m
1m
生活实例:
对楼梯倾斜程度的认识
坡度=
高度
宽度
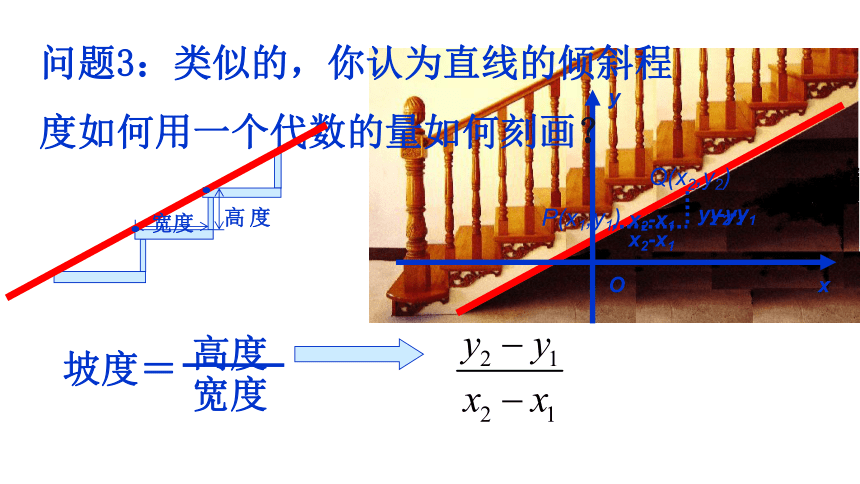
问题3:类似的,你认为直线的倾斜程
度如何用一个代数的量如何刻画?
坡度=
高度
宽度
x
y
O
P(x1,y1)
Q(x2,y2)
宽度
度高
y2-y1
x2-x1
x2-x1
y2-y1
x
y
o
是一个定值
思考1:P,Q交换位置 的值会改变吗?
P
Q
P’
Q’
M
M’
问题4: 适用所有的直线吗?
思考2:P,Q位置发生变化, 的值会改变吗?
x
y
o
形
数
已知两点 P(x1,y1), Q(x2,y2),如果 x1≠x2,我们把比值 叫做直 线的斜率。
x1≠x2
不存在
数学应用1
如图直线 都经过点 ,
又 分别经过点
讨论 斜率是否存在,如存在,求出直线的斜率.
x
y
o
l1
l2
l3
l4
P
Q1
Q2
Q3
Q4
k1=1
k2=-1
k3=0
斜率不存在
经过点A(3,2)画直线,使直线的斜率分别为①0,②不存在,③ ,④ 。
A(3,2)
x
y
o
2
3
1
1
3
2
x
y
o
2
3
1
1
3
2
A(3,2)
x
y
o
2
3
1
1
3
2
A(3,2)
C(6,0)
2
数学应用2
2.直线的倾斜角
在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.
规定:与x轴平行或重合的直线的倾斜角为______.
问题5
你能说出下列直线的倾斜角吗?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
思考1:直线的倾斜角的范围是?
思考2:直线的倾斜角与斜率有什么关系?
3.当直线与x轴不垂直时,直线的斜率k与倾斜角α的关系式为:
数学应用3
?
0
k=0
k>0
k<0
当堂反馈:
1.分别求经过下列两点的直线的斜率:
(1)(3,-1),(2,-1)
(2)(a+1,a-1),(a,a)
2.分别判断下列三点是否在同一条直线上:
(1)(-1,4),(2,1),(-2,5)
(2)(1,2),(2,3),(3,7)
(3)(1,0),(1,3),(1,-1)
0
-1
是
不是
是
THANKS
THANK YOU FOR YOUR ATTENTION
小结:
1.直线的斜率;
2.直线的倾斜角;
3.直线的斜率与倾斜角的关系
江苏省宝应中学
平面解析几何,就是通过引进直角坐标系,建立点与坐标、曲线与方程之间的对应关系,将几何问题转化为代数问题,从而用代数方法研究几何问题.充分体现了数形结合的数学思想。
直 线 的 斜 率
问题1:
(1)一块长方形的钢板ABCD,你能
画出它的对角线BD吗?
(2)
你能总结一下,如何才能确定一条直线吗?
问题2:通过建立直角坐标系,点可以用坐标来刻画,那么,直线的倾斜程度如何用一个代数的量来刻画呢?
.
.
.
x
y
o
y
x
o
结论:坡度越大,楼梯越陡.
0.8m
1m
0.4m
1m
生活实例:
对楼梯倾斜程度的认识
坡度=
高度
宽度
问题3:类似的,你认为直线的倾斜程
度如何用一个代数的量如何刻画?
坡度=
高度
宽度
x
y
O
P(x1,y1)
Q(x2,y2)
宽度
度高
y2-y1
x2-x1
x2-x1
y2-y1
x
y
o
是一个定值
思考1:P,Q交换位置 的值会改变吗?
P
Q
P’
Q’
M
M’
问题4: 适用所有的直线吗?
思考2:P,Q位置发生变化, 的值会改变吗?
x
y
o
形
数
已知两点 P(x1,y1), Q(x2,y2),如果 x1≠x2,我们把比值 叫做直 线的斜率。
x1≠x2
不存在
数学应用1
如图直线 都经过点 ,
又 分别经过点
讨论 斜率是否存在,如存在,求出直线的斜率.
x
y
o
l1
l2
l3
l4
P
Q1
Q2
Q3
Q4
k1=1
k2=-1
k3=0
斜率不存在
经过点A(3,2)画直线,使直线的斜率分别为①0,②不存在,③ ,④ 。
A(3,2)
x
y
o
2
3
1
1
3
2
x
y
o
2
3
1
1
3
2
A(3,2)
x
y
o
2
3
1
1
3
2
A(3,2)
C(6,0)
2
数学应用2
2.直线的倾斜角
在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.
规定:与x轴平行或重合的直线的倾斜角为______.
问题5
你能说出下列直线的倾斜角吗?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
思考1:直线的倾斜角的范围是?
思考2:直线的倾斜角与斜率有什么关系?
3.当直线与x轴不垂直时,直线的斜率k与倾斜角α的关系式为:
数学应用3
?
0
k=0
k>0
k<0
当堂反馈:
1.分别求经过下列两点的直线的斜率:
(1)(3,-1),(2,-1)
(2)(a+1,a-1),(a,a)
2.分别判断下列三点是否在同一条直线上:
(1)(-1,4),(2,1),(-2,5)
(2)(1,2),(2,3),(3,7)
(3)(1,0),(1,3),(1,-1)
0
-1
是
不是
是
THANKS
THANK YOU FOR YOUR ATTENTION
小结:
1.直线的斜率;
2.直线的倾斜角;
3.直线的斜率与倾斜角的关系
