湘教版九年级数学下册第2章:圆 单元测试(含答案)
文档属性
| 名称 | 湘教版九年级数学下册第2章:圆 单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 10:30:23 | ||
图片预览




文档简介
九年级圆单元测试附答案
一、选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.下列说法正确的是
A.长度相等的两条弧是等弧 B.平分弦的直径垂直于弦
C.直径是同一个圆中最长的弦 D.过三点能确定一个圆
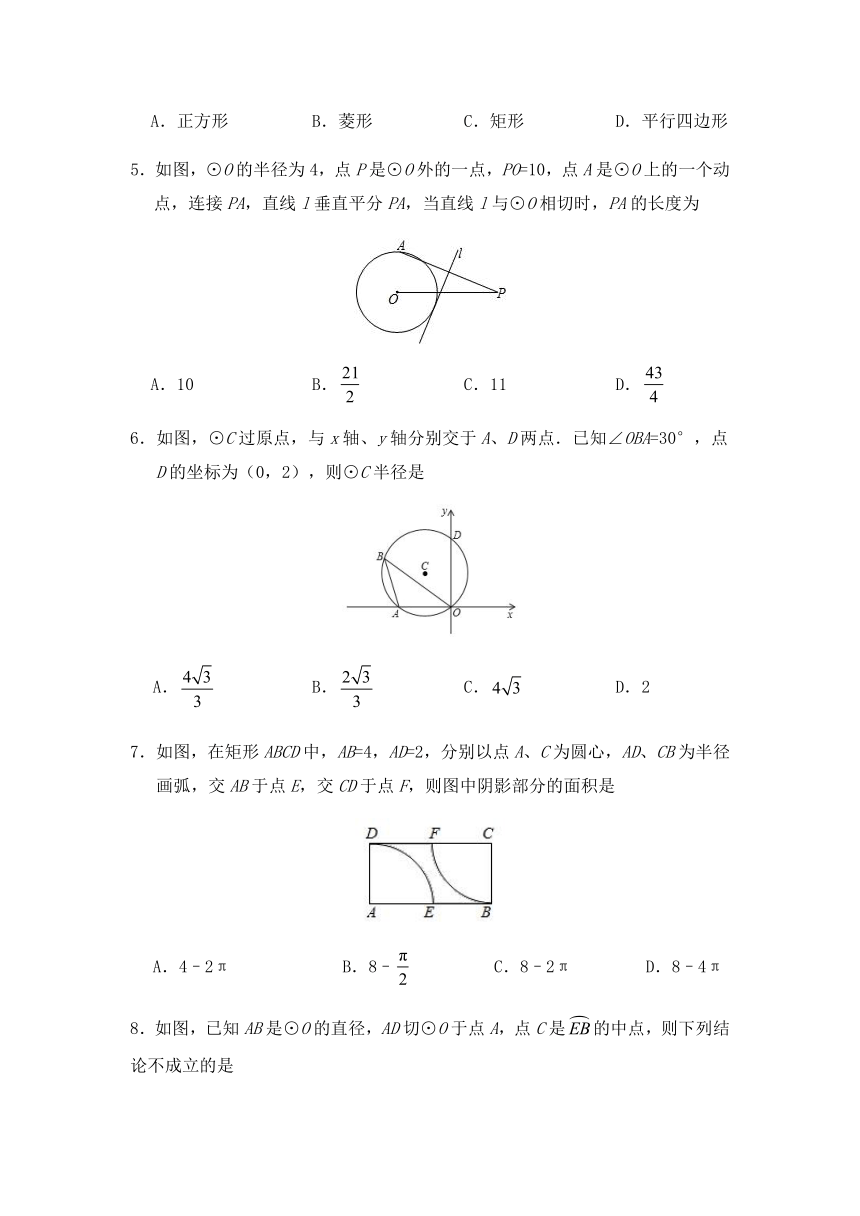
2.如图,在半径为5 cm的⊙O中,弦AB=6 cm,OC⊥AB于点C,则OC=
A.3 cm B.4 cm C.5 cm D.6 cm
3.如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为
A.46° B.47° C.48° D.49°
4.如图,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,则四边形OEAD为
A.正方形 B.菱形 C.矩形 D.平行四边形
5.如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为
A.10 B. C.11 D.
6.如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是
A. B. C. D.2
7.如图,在矩形ABCD中,AB=4,AD=2,分别以点A、C为圆心,AD、CB为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是
A.4–2π B.8– C.8–2π D.8–4π
8.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
二、填空题(本大题共4个小题,每小题6分,共24分)
9.一个扇形的面积是12π cm?,圆心角是60°,则此扇形的半径是________cm.
10.如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧的长度为__________.
11.如图,⊙O的半径是4,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为__________.
12.如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.
(1)半圆=________; (2)BP的最大值是________.
三、解答题(本大题共3个小题,每小题12分,共36分. 解答应写出文字说明、证明过程或演算步骤)
13.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;(2)求证:PCE是等腰三角形.
14.如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=,求AE的值.
15.已知ABC内接于⊙O,AC是⊙O的直径,D是的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积。
一、选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.下列说法正确的是
A.长度相等的两条弧是等弧 B.平分弦的直径垂直于弦
C.直径是同一个圆中最长的弦 D.过三点能确定一个圆
【答案】C【解析】要找出正确命题,可运用相关基础知识分析找出正确选项,也可以通过举反例排除不正确选项,从而得出正确选项.对于选项A,在同圆或等圆中,长度相等的两条弧是等弧,所以A错误.对于选项B,平分弦(不是直径)的直径垂直于弦,所以B错误;对于选项C,直径是同一个圆中最长的弦,所以C正确;对于选项D,过不在同一直线上的三点能确定一个圆,所以D错误.故选C.
2.如图,在半径为5 cm的⊙O中,弦AB=6 cm,OC⊥AB于点C,则OC=
A.3 cm B.4 cm C.5 cm D.6 cm
【答案】B【解析】如图,连接OA,∵OC⊥AB,∴AC=AB=3 cm,∴OC==4(cm).故选B.
3.如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为
A.46° B.47° C.48° D.49°
【答案】C【解析】∵OB=OC,∴∠B=∠BCO=21°,∴∠AOD=∠B+∠BCO=21°+21°=42°,∵AB是⊙O的直径,直线DA与⊙O相切于点A,∴∠OAD=90°,∴∠ADC=90°–∠AOD=90°–42°=48°.故选C.
4.如图,在⊙O中,相等的弦AB、AC互相垂直,OE⊥AC于E,OD⊥AB于D,则四边形OEAD为
A.正方形 B.菱形 C.矩形 D.平行四边形
【答案】A【解析】由OD⊥AB,OE⊥AC得到AD=AB,AE=AC,且∠ADO=∠AEO=90°,又∠DAE=90°,则四边形ADOE是矩形,由于AB=AC,所以AD=AE,所以矩形ADOE是正方形.故选A.
5.如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为
A.10 B. C.11 D.
【答案】B【解析】如图.连接OA、OC(C为切点),过点O作OB⊥AP.
设AB的长为x,在RtAOB中,OB2=OA2–AB2=16–x2,∵l与⊙O相切,∴OC⊥l.
∵∠OBD=∠OCD=∠CDB=90°,∴四边形BOCD为矩形.∴BD=OC=4.∵直线l垂直平分PA,
∴PD=BD+AB=4+x.∴PB=8+x.在RtOBP中,OP2=OB2+PB2,即16﹣x2+(8+x)2=102,解得x= .
PA=2AD=2×(+4)= .故选B.
6.如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是
A. B. C. D.2
【答案】B【解析】连接AD.∵∠AOD=90°,∴AD是圆的直径.在直角三角形AOD中,∠D=∠B=30°,OD=2,∴AD==.则圆的半径是.故选B.
7.如图,在矩形ABCD中,AB=4,AD=2,分别以点A、C为圆心,AD、CB为半径画弧,交AB于点E,交CD于点F,则图中阴影部分的面积是
A.4–2π B.8– C.8–2π D.8–4π
【答案】C【解析】∵矩形ABCD,∴AD=CB=2,∴S阴影=S矩形–S半圆=2×4–π×22=8–2π,故选C.
8.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
【答案】D【解析】A、∵点C是的中点,∴OC⊥BE,∵AB为圆O的直径,∴AE⊥BE,∴OC∥AE,本选项正确;B、∵,∴BC=CE,本选项正确;C、∵AD为圆O的切线,∴AD⊥OA,∴∠DAE+∠EAB=90°,∵∠EBA+∠EAB=90°,∴∠DAE=∠EBA,本选项正确;D、AC不一定垂直于OE,本选项错误,故选D.
二、填空题(本大题共4个小题,每小题6分,共24分)
9.一个扇形的面积是12π cm?,圆心角是60°,则此扇形的半径是________cm.
【答案】【解析】设这个扇形的半径是r cm.根据扇形面积公式,得 ,解得(负值舍去),故填.
10.如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧的长度为__________.
【答案】【解析】连接OA、OC,如图.∵五边形ABCDE是正五边形,∴∠E=∠D==108°.
∵AE、CD与⊙O相切,∴∠OAE=∠OCD=90°,∴∠AOC=(5–2)×180°–90°–108°–108°–90°=144°,∴的长为=.故答案为.
11.如图,⊙O的半径是4,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为__________.
【答案】【解析】连接OC,如图,∵OG⊥AC,∴CG=AG,在Rt△OCG中,CG===,∴AC=2CG=2,∵OE⊥AB,OF⊥BC,∴AE=BE,BF=CF,∴EF为△BAC的中位线,∴EF=AC
=.故答案为.
12.如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.
(1)半圆=________; (2)BP的最大值是________.
【答案】(1)2π;(2)2+
【解析】(1)∵矩形ABCD中,AB=CD,AB=4,∴CD=4, (2)当BP经过CD的中点时,BP最长,∵AB=4,AD=3,∴BC=3,OC=2,∴OB=,∵OP=2,∴BP=2+.
故答案为(1)2π; (2)2+.
三、解答题(本大题共3个小题,每小题12分,共36分. 解答应写出文字说明、证明过程或演算步骤)
13.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:PCE是等腰三角形.
【解析】(1)如图,连接OC,
∵PD切⊙O于点C,∴OC⊥PD. (2分)
又∵AD⊥PD,∴OC∥AD.∴∠ACO=∠DAC.
又∵OC=OA,∴∠ACO=∠CAO,∴∠DAC=∠CAO,
即AC平分∠DAB. (5分)
(2)∵AD⊥PD,∴∠DAC+∠ACD=90°.
又∵AB为⊙O的直径,∴∠ACB=90°.(7分)
∴∠PCB+∠ACD=90°,∴∠DAC=∠PCB.
又∵∠DAC=∠CAO,∴∠CAO=∠PCB.(9分)
∵CE平分∠ACB,∴∠ACE=∠BCE,
∴∠CAO+∠ACE=∠PCB+∠BCE,
∴∠PEC=∠PCE,∴PC=PE,
即PCE是等腰三角形.(12分)
