高中数学人教A版必修2第二章第21节《直线的两点式方程》课件(共37张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第二章第21节《直线的两点式方程》课件(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 816.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 21:06:59 | ||
图片预览









文档简介
(共37张PPT)
2.1.2 直线的两点式方程
江苏省宝应中学
形式 条件 直线方程 应用范围
点斜式 直线过点(x0, y0),
且斜率为k
斜截式 在y轴上的截距为b,且斜率为k
斜率存在的直线
斜率存在的直线
知识回顾:
1.理解直线的两点式方程形式,知道截距式是两点式的特例.
2.掌握直线方程的两点式、截距式以及它们之间的联系和转化,并能根据条件熟练地求出满足已知条件的直线方程.
知识链接:
分别求出经过下列两点的直线方程:
x
y
O
1
两点确定一条直线!那么经过两个定点的直线方程能否用“公式”直接写出来?
知识引入:
如图所示,已知直线L上两点A(x1,y1),B(x2,y2)(其中x1≠x2),求直线L的方程.
知识构建:
A(x1,y1)
0
●
●
B(x2,y2)
x
y
(2)给出线L的方程.
(由点斜式方程得):
y-y0=k(x-x0)
(1)求直线L的斜率k.
这个方程还是体现的点斜式的特点,那么这个方程还能变形为哪些形式?
方案1:
(x2-x1)(y-y1)-(y2-y1)(x-x1)=0
这个形式的方程与点斜式的形式又什么本质的差别呢?有什么优缺点呢?
将x2-x1乘到方程左边,这样就可以有x1=x2;优点是可以表示任何直线;缺点是:仍然不能体现两点的特点。
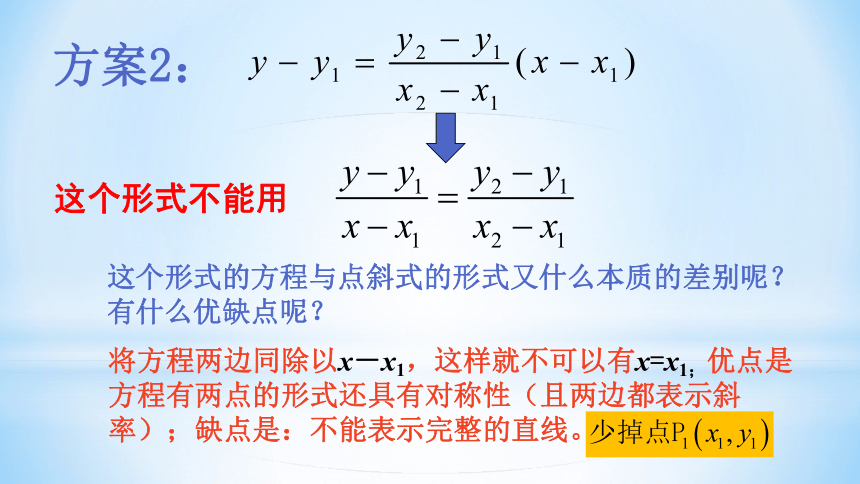
方案2:
这个形式的方程与点斜式的形式又什么本质的差别呢?有什么优缺点呢?
将方程两边同除以x-x1,这样就不可以有x=x1;优点是方程有两点的形式还具有对称性(且两边都表示斜率);缺点是:不能表示完整的直线。
这个形式不能用
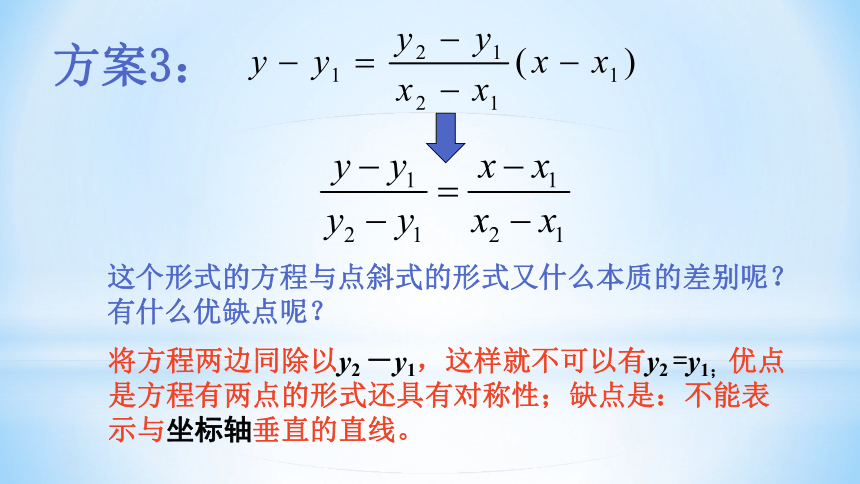
方案3:
这个形式的方程与点斜式的形式又什么本质的差别呢?有什么优缺点呢?
将方程两边同除以y2 -y1,这样就不可以有y2 =y1;优点是方程有两点的形式还具有对称性;缺点是:不能表示与坐标轴垂直的直线。
通过对三种方案的分析,方案三的形式更适合作为直线的两点式方程。
体会形式的特点:
两点式适用于:
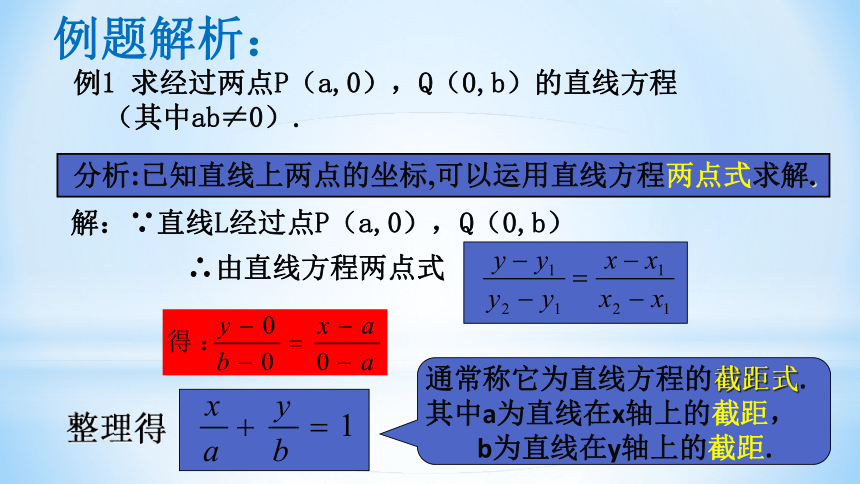
解:∵直线L经过点P(a,0),Q(0,b)
∴由直线方程两点式
例1 求经过两点P(a,0),Q(0,b)的直线方程 (其中ab≠0).
整理得
通常称它为直线方程的截距式.
其中a为直线在x轴上的截距,
b为直线在y轴上的截距.
分析:已知直线上两点的坐标,可以运用直线方程两点式求解.
例题解析:
P(a,0)
x
y
0
Q(0,b)
●
●
x轴上的截距a
y
轴
上
的
截
距
b
由截距式可得到过
P点和Q点的直线方程
数形结合来理解
概念理解:
答案:与x轴或与y轴
答案:-3 2
题型一 求直线的两点式方程
例2. 三角形的顶点A(-5,0),B(3,-3),C(0,2),求这个三角形三边所在直线的方程.
跟踪训练:
解:
所以AB边中线所在直线方程为
另解:
∵ AB 边中线过 AB 边中点M 和△ABC 的重心 ,
题型二 求直线的截距式方程
例4. 直线l过点(-3,4),且在两坐标轴上的截距之和为12,求直线l的方程.
跟踪训练:
知识小结:
1.体会在已有知识的基础上变化可以发现新知识的过程:是探索和发现的过程、是知识完善和推进的过程;
2.数形结合在学习数学过程中的重要性:形可以弥补我们单从数或者式角度理解和处理问题时产生的盲区和误区。
学法小结:
谢谢聆听!
2.1.2 直线的两点式方程
江苏省宝应中学
形式 条件 直线方程 应用范围
点斜式 直线过点(x0, y0),
且斜率为k
斜截式 在y轴上的截距为b,且斜率为k
斜率存在的直线
斜率存在的直线
知识回顾:
1.理解直线的两点式方程形式,知道截距式是两点式的特例.
2.掌握直线方程的两点式、截距式以及它们之间的联系和转化,并能根据条件熟练地求出满足已知条件的直线方程.
知识链接:
分别求出经过下列两点的直线方程:
x
y
O
1
两点确定一条直线!那么经过两个定点的直线方程能否用“公式”直接写出来?
知识引入:
如图所示,已知直线L上两点A(x1,y1),B(x2,y2)(其中x1≠x2),求直线L的方程.
知识构建:
A(x1,y1)
0
●
●
B(x2,y2)
x
y
(2)给出线L的方程.
(由点斜式方程得):
y-y0=k(x-x0)
(1)求直线L的斜率k.
这个方程还是体现的点斜式的特点,那么这个方程还能变形为哪些形式?
方案1:
(x2-x1)(y-y1)-(y2-y1)(x-x1)=0
这个形式的方程与点斜式的形式又什么本质的差别呢?有什么优缺点呢?
将x2-x1乘到方程左边,这样就可以有x1=x2;优点是可以表示任何直线;缺点是:仍然不能体现两点的特点。
方案2:
这个形式的方程与点斜式的形式又什么本质的差别呢?有什么优缺点呢?
将方程两边同除以x-x1,这样就不可以有x=x1;优点是方程有两点的形式还具有对称性(且两边都表示斜率);缺点是:不能表示完整的直线。
这个形式不能用
方案3:
这个形式的方程与点斜式的形式又什么本质的差别呢?有什么优缺点呢?
将方程两边同除以y2 -y1,这样就不可以有y2 =y1;优点是方程有两点的形式还具有对称性;缺点是:不能表示与坐标轴垂直的直线。
通过对三种方案的分析,方案三的形式更适合作为直线的两点式方程。
体会形式的特点:
两点式适用于:
解:∵直线L经过点P(a,0),Q(0,b)
∴由直线方程两点式
例1 求经过两点P(a,0),Q(0,b)的直线方程 (其中ab≠0).
整理得
通常称它为直线方程的截距式.
其中a为直线在x轴上的截距,
b为直线在y轴上的截距.
分析:已知直线上两点的坐标,可以运用直线方程两点式求解.
例题解析:
P(a,0)
x
y
0
Q(0,b)
●
●
x轴上的截距a
y
轴
上
的
截
距
b
由截距式可得到过
P点和Q点的直线方程
数形结合来理解
概念理解:
答案:与x轴或与y轴
答案:-3 2
题型一 求直线的两点式方程
例2. 三角形的顶点A(-5,0),B(3,-3),C(0,2),求这个三角形三边所在直线的方程.
跟踪训练:
解:
所以AB边中线所在直线方程为
另解:
∵ AB 边中线过 AB 边中点M 和△ABC 的重心 ,
题型二 求直线的截距式方程
例4. 直线l过点(-3,4),且在两坐标轴上的截距之和为12,求直线l的方程.
跟踪训练:
知识小结:
1.体会在已有知识的基础上变化可以发现新知识的过程:是探索和发现的过程、是知识完善和推进的过程;
2.数形结合在学习数学过程中的重要性:形可以弥补我们单从数或者式角度理解和处理问题时产生的盲区和误区。
学法小结:
谢谢聆听!
