人教A版数学必修四第一章三角函数知识点复习(共20张PPT)
文档属性
| 名称 | 人教A版数学必修四第一章三角函数知识点复习(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
三角函数的复习
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1. 构成的三个要素:
任意角和弧度制
顶点、始边、终边
2. 任意角:
正角(逆时针)、负角(顺时针)、零角(没有旋转)
3. 象限角:
条件:顶点与原点重合,角的始边与x轴的非负半轴重合
角的终边在第几象限,就说是第几象限角
角的终边在坐标轴上,角不属于任何一个象限
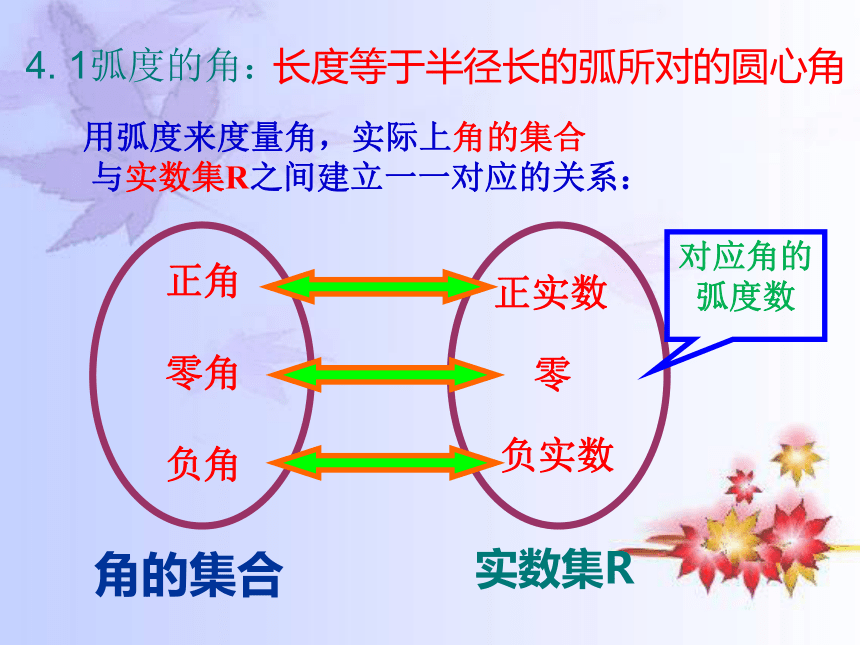
4. 1弧度的角:
长度等于半径长的弧所对的圆心角
用弧度来度量角,实际上角的集合
与实数集R之间建立一一对应的关系:
对应角的弧度数
公式
角 弧度数的绝对值:
同角三角函数的基本关系
某些变式的运用
三角函数的定义
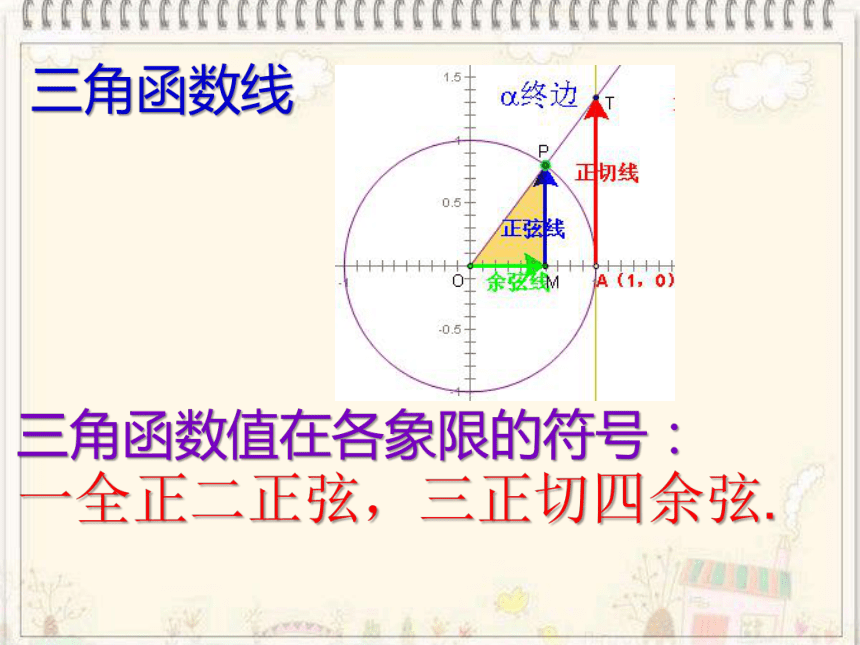
三角函数值在各象限的符号:
一全正二正弦,三正切四余弦.
三角函数线
诱导公式(一)
实质:终边相同,三角函数值相等
用途:“大”角化“小”角
函数名不变,符号看象限
(1)α是任意角
函数名改变,符号看象限
解题一般步骤
负角
正角
0~2π
0~π
锐角
小结
1.运用诱导公式可以将任意角三角函数转化为锐角三角函数.
2.公式一至四:函数名不变,符号看象限;
3.公式五、六:函数名改变,符号看象限;
4. , 的三角函数值之间的关系 :
奇变偶不变,符号看象限.
注:奇、偶指的是 的值;变、不变是指的是函数名.
奇函数
偶函数
函数 y=sinx y=cosx
图形
定义域
值域
最值
单调性
奇偶性
周期
对称性
⑴ 定义域:
⑵ 值域:
⑶ 周期性:
⑷ 奇偶性:
正
切
函
数
图
像
奇函数,图象关于原点对称。
R
⑸ 单调性:
(6)渐近线方程:
(7)对称中心
*
观察函数 的图象和 y=sinx 的图象的 关系.
模拟试验
*
y=sinx
的图象
法一:
◆思考:还有其他的变换方法吗?
*
y=sinx
的图象
法二:
*
y=Asinx, x?R(A>0,A ? 1)的图象可以由y=sinx的图象所有点的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍,横坐标不变得到。值域为[-A,A]
A ——振幅变换
y=sin?x, x?R(?>0,??1)的图象可以由y=sinx的图象所有点的横坐标伸长(?<1)或缩短(?>1)原来的1/?倍,纵坐标不变得到。
? ——周期变换
? ——相位变换
y=sin(x+?), x?R(? ? 0)的图象可以由y=sinx的图象上所有点向左(? >0)或向右(? <0)平移| ? |个单位,纵坐标不变得到。
*
周期变换
y=sinωx
相位变换
y=sin(x+?)
y=sinx
y=sin(ωx+?)
周期变换
振幅变换
y=Asin(ωx+?)
无论周期变换还是相位变换都是直接作用在x上的!!!
在先经过周期变换,再进行相位变换的时候,实际平移的是?/?个单位。
相位变换
三角函数的复习
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1. 构成的三个要素:
任意角和弧度制
顶点、始边、终边
2. 任意角:
正角(逆时针)、负角(顺时针)、零角(没有旋转)
3. 象限角:
条件:顶点与原点重合,角的始边与x轴的非负半轴重合
角的终边在第几象限,就说是第几象限角
角的终边在坐标轴上,角不属于任何一个象限
4. 1弧度的角:
长度等于半径长的弧所对的圆心角
用弧度来度量角,实际上角的集合
与实数集R之间建立一一对应的关系:
对应角的弧度数
公式
角 弧度数的绝对值:
同角三角函数的基本关系
某些变式的运用
三角函数的定义
三角函数值在各象限的符号:
一全正二正弦,三正切四余弦.
三角函数线
诱导公式(一)
实质:终边相同,三角函数值相等
用途:“大”角化“小”角
函数名不变,符号看象限
(1)α是任意角
函数名改变,符号看象限
解题一般步骤
负角
正角
0~2π
0~π
锐角
小结
1.运用诱导公式可以将任意角三角函数转化为锐角三角函数.
2.公式一至四:函数名不变,符号看象限;
3.公式五、六:函数名改变,符号看象限;
4. , 的三角函数值之间的关系 :
奇变偶不变,符号看象限.
注:奇、偶指的是 的值;变、不变是指的是函数名.
奇函数
偶函数
函数 y=sinx y=cosx
图形
定义域
值域
最值
单调性
奇偶性
周期
对称性
⑴ 定义域:
⑵ 值域:
⑶ 周期性:
⑷ 奇偶性:
正
切
函
数
图
像
奇函数,图象关于原点对称。
R
⑸ 单调性:
(6)渐近线方程:
(7)对称中心
*
观察函数 的图象和 y=sinx 的图象的 关系.
模拟试验
*
y=sinx
的图象
法一:
◆思考:还有其他的变换方法吗?
*
y=sinx
的图象
法二:
*
y=Asinx, x?R(A>0,A ? 1)的图象可以由y=sinx的图象所有点的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍,横坐标不变得到。值域为[-A,A]
A ——振幅变换
y=sin?x, x?R(?>0,??1)的图象可以由y=sinx的图象所有点的横坐标伸长(?<1)或缩短(?>1)原来的1/?倍,纵坐标不变得到。
? ——周期变换
? ——相位变换
y=sin(x+?), x?R(? ? 0)的图象可以由y=sinx的图象上所有点向左(? >0)或向右(? <0)平移| ? |个单位,纵坐标不变得到。
*
周期变换
y=sinωx
相位变换
y=sin(x+?)
y=sinx
y=sin(ωx+?)
周期变换
振幅变换
y=Asin(ωx+?)
无论周期变换还是相位变换都是直接作用在x上的!!!
在先经过周期变换,再进行相位变换的时候,实际平移的是?/?个单位。
相位变换
