人教版八年级数学下册 17.1勾股定理 课件 (共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册 17.1勾股定理 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 854.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 12:05:45 | ||
图片预览




文档简介
(共20张PPT)
17.1勾股定理(1)
讲师:初二X班XXX
观察——发现
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了直角三角形三边的关系。
A
B
C
c
a
b
两直角边的平方和等于斜边的平方
面积A+面积B=面积C
a2 + b2 = c2
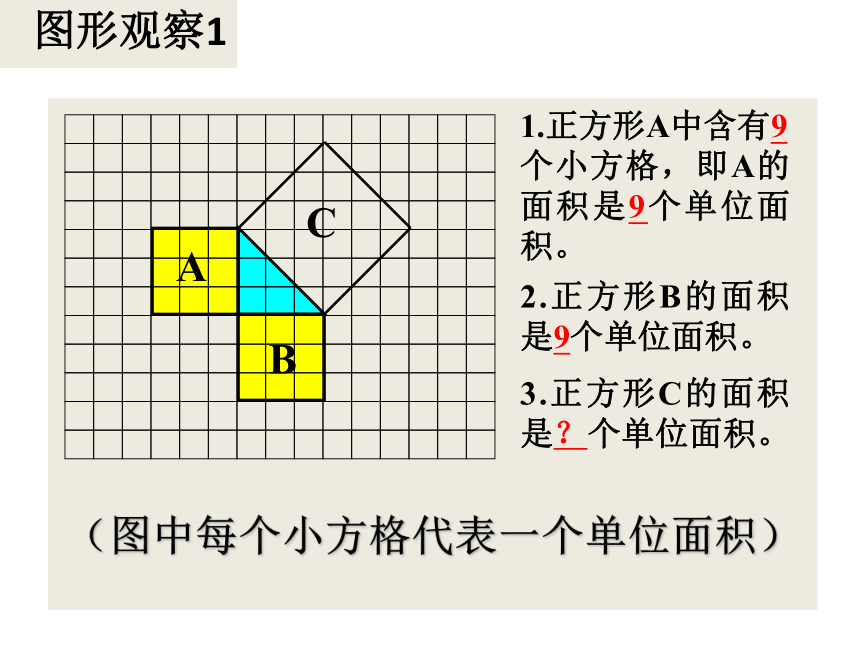
图形观察1
A
B
C
1.正方形A中含有9 个小方格,即A的面积是9个单位面积。
2.正方形B的面积是9个单位面积。
3.正方形C的面积是?个单位面积。
(图中每个小方格代表一个单位面积)
图形观察2
A
B
C
图2-1
(单位面积)
(图中每个小方格代表一个单位面积)
分“割”成若干个直
角边为整数的三角形
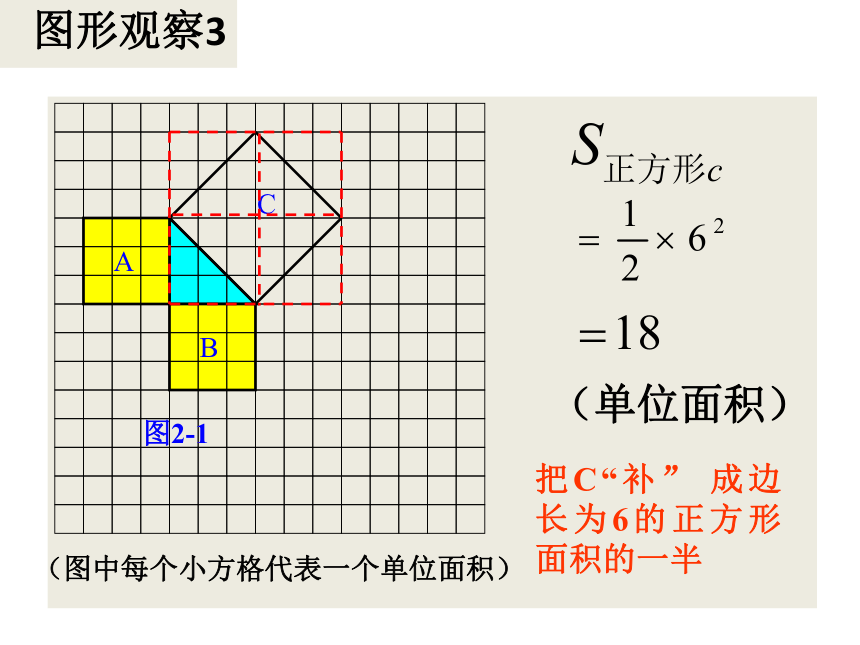
图形观察3
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
(单位面积)
把C“补” 成边长为6的正方形面积的一半
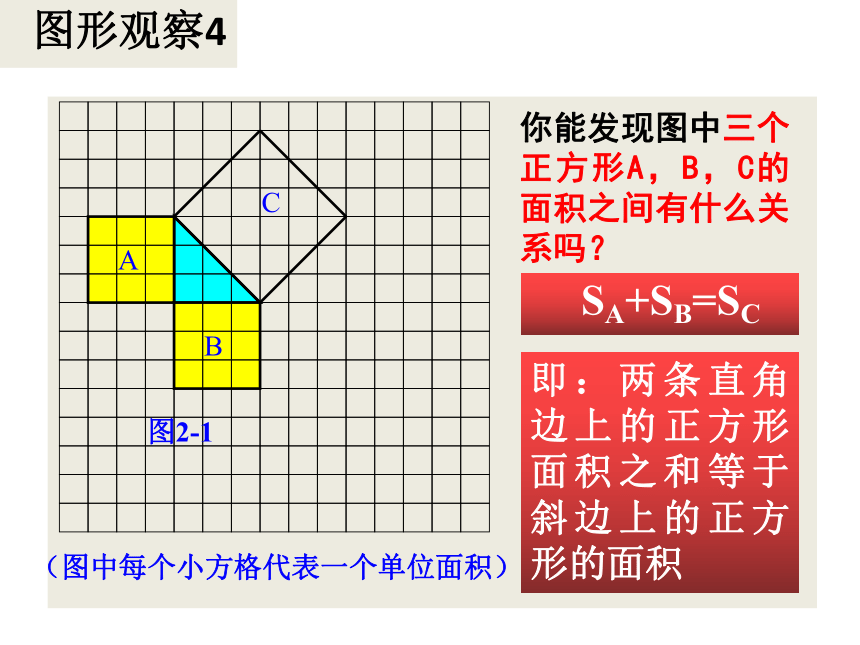
图形观察4
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
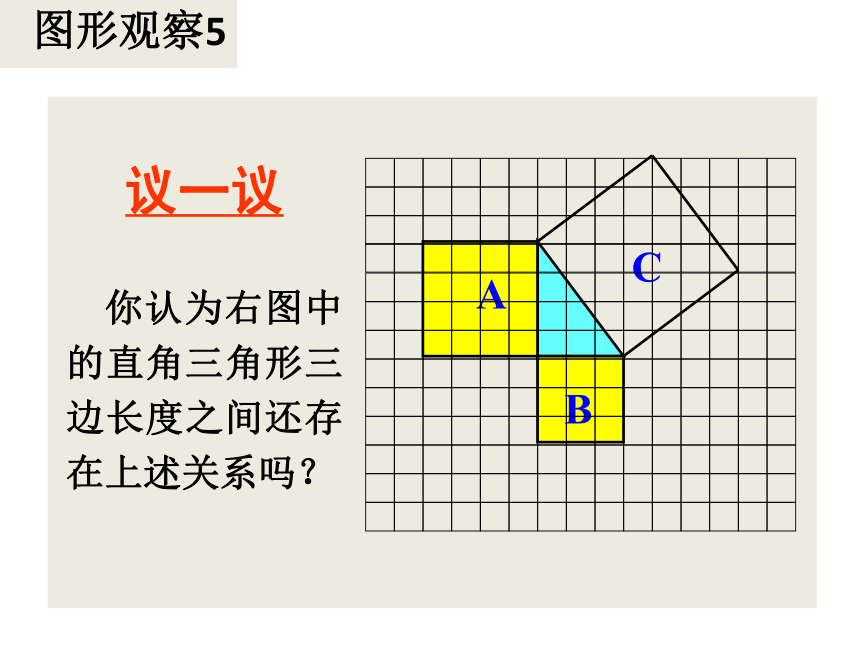
图形观察5
A
B
C
你认为右图中的直角三角形三边长度之间还存在上述关系吗?
议一议
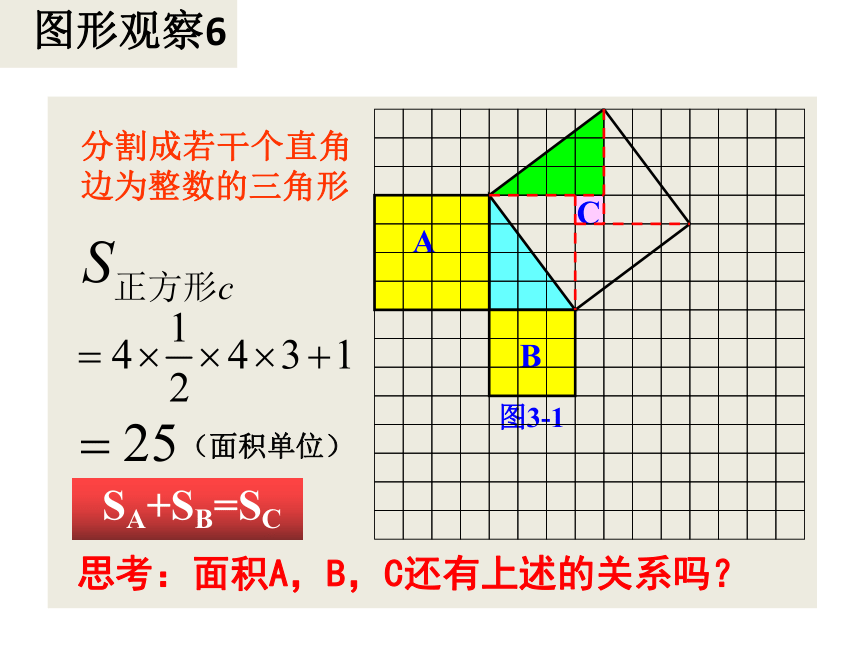
图形观察6
A
B
C
图3-1
分割成若干个直角边为整数的三角形
(面积单位)
思考:面积A,B,C还有上述的关系吗?
SA+SB=SC
观察所得到的各组数据,你有什么发现?
A
B
C
a
c
b
Sa+Sb=Sc
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
命题猜想
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么c2=a2+b2。
a
b
c
勾
股
弦
猜测研究
尝试用下面四个全等的直角三角形围成一个正方形。
a
b
c
b
c
b
c
b
c
a
a
a
第一种拼法
c
a
b
c
a
b
c
a
b
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4? ab/2+(b- a)2
∵ c2= 4?ab/2 +(b-a)2
第二种拼法
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
(a+b)2
c2 +4?ab/2
大正方形的面积可以表为 也可以表示为
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形两直角边的平方和等于斜边的平方
课堂演练
求图中直角三角形的未知边的长度。
8
6
A
B
C
AC2=AB2+BC2=62+82=100
∴AC=√100 = 10
在Rt△ABC中,根据勾股定理,
课堂演练
求图中直角三角形的未知边的长度。
15
17
BC2=AC2-AB2=172-152=64
∴BC=√64= 8
在Rt△ABC中,根据勾股定理,
A
B
C
课堂探究
=625
225
400
A
225
81
B
=144
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积。
课堂探究
2.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为__49__cm2。
A
B
C
D
7cm
谢 谢 观 看
17.1勾股定理(1)
讲师:初二X班XXX
观察——发现
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了直角三角形三边的关系。
A
B
C
c
a
b
两直角边的平方和等于斜边的平方
面积A+面积B=面积C
a2 + b2 = c2
图形观察1
A
B
C
1.正方形A中含有9 个小方格,即A的面积是9个单位面积。
2.正方形B的面积是9个单位面积。
3.正方形C的面积是?个单位面积。
(图中每个小方格代表一个单位面积)
图形观察2
A
B
C
图2-1
(单位面积)
(图中每个小方格代表一个单位面积)
分“割”成若干个直
角边为整数的三角形
图形观察3
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
(单位面积)
把C“补” 成边长为6的正方形面积的一半
图形观察4
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
图形观察5
A
B
C
你认为右图中的直角三角形三边长度之间还存在上述关系吗?
议一议
图形观察6
A
B
C
图3-1
分割成若干个直角边为整数的三角形
(面积单位)
思考:面积A,B,C还有上述的关系吗?
SA+SB=SC
观察所得到的各组数据,你有什么发现?
A
B
C
a
c
b
Sa+Sb=Sc
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
命题猜想
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么c2=a2+b2。
a
b
c
勾
股
弦
猜测研究
尝试用下面四个全等的直角三角形围成一个正方形。
a
b
c
b
c
b
c
b
c
a
a
a
第一种拼法
c
a
b
c
a
b
c
a
b
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4? ab/2+(b- a)2
∵ c2= 4?ab/2 +(b-a)2
第二种拼法
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4?ab/2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
(a+b)2
c2 +4?ab/2
大正方形的面积可以表为 也可以表示为
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形两直角边的平方和等于斜边的平方
课堂演练
求图中直角三角形的未知边的长度。
8
6
A
B
C
AC2=AB2+BC2=62+82=100
∴AC=√100 = 10
在Rt△ABC中,根据勾股定理,
课堂演练
求图中直角三角形的未知边的长度。
15
17
BC2=AC2-AB2=172-152=64
∴BC=√64= 8
在Rt△ABC中,根据勾股定理,
A
B
C
课堂探究
=625
225
400
A
225
81
B
=144
1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积。
课堂探究
2.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为__49__cm2。
A
B
C
D
7cm
谢 谢 观 看
