青岛版数学七年级下册13.3 圆(2) 课件(16张ppt)
文档属性
| 名称 | 青岛版数学七年级下册13.3 圆(2) 课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 16:35:01 | ||
图片预览





文档简介
课件16张PPT。13.3 圆(2)青岛版数学七年级下册温故知新1.用描述性语言叙述“圆”是怎样形成的?
2.用集合的观点来描述圆的概念
3.在平面内,一个点与一个圆有怎样的位置关
系?(用画图的方法展示一下)
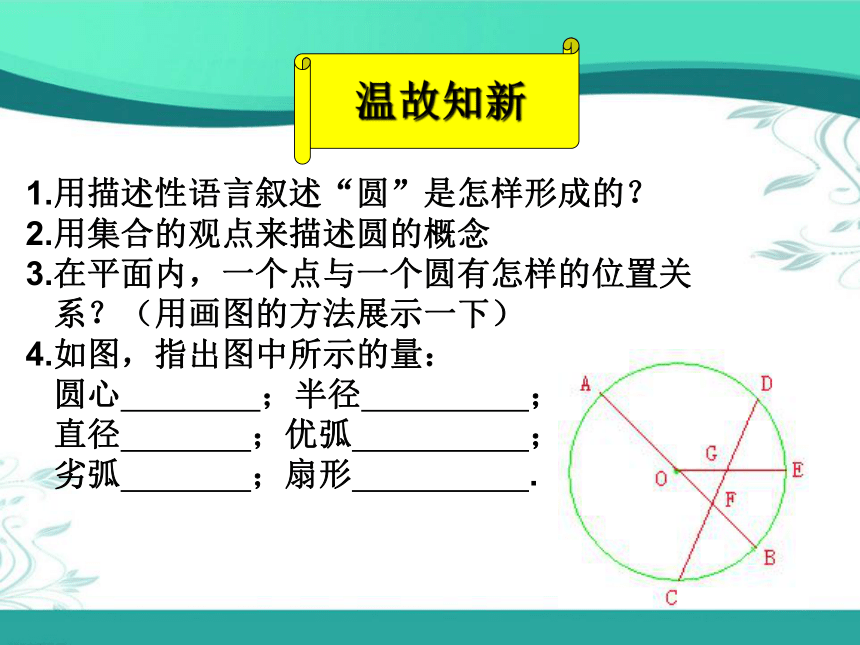
4.如图,指出图中所示的量:
圆心 ;半径 ;
直径 ;优弧 ;
劣弧 ;扇形 .学 习 目 标1.理解等圆、同心圆、等弧、圆环等概念;
2.会用圆的面积与周长公式进行有关简单
问题的计算;
3.会利用圆的有关知识解决与圆有关的问题.实验与探究 分别观察图(1)与图(2),你发现图(1)中的两枚硬币所确定的两个圆有什么特点(也可以自己取两枚相同硬币来观察)?图(2)中的几个圆有什么共同点和不同点?能够重合的圆叫做等圆圆心相同、半径不等的圆叫做同心圆交流与发现问题1 各小组由一名同学说出一个数字,然后每个人都以这个数字为半径做一个圆,然后同学之间相互将所画的圆重叠,看看有什么发现?然后和其他小组交流
你们小组的发现是:
其他小组和你们小组的发现相同吗?只要是半径确定了,所画的圆均能够重合 虽然每个小组在画圆时半径不相同,但各自所画的圆
都能够重合相同问题2 判断:能够重合的两段弧就是等弧对吗?
那必须具备怎样的条件的弧才是等弧呢?
试一试找出下图中的等弧 在等圆或同圆中,能够互
相重合的弧叫做 等弧问题3 你能用圆规作出几个圆心相同但半径不同
的圆吗?试试看!
(这样的圆课本上给它们取了怎么有趣的名字?) 同心圆问题4 讨论:由问题3,我们知道由两个圆心相同但半径不同的两个圆就组成同心圆,我们把两个同心圆之间的部分叫做圆环,那么你能用图形表示“到点A的距离大于2厘米而小于3厘米的点的集合”吗?解:如图,为两圆之间的圆环部分(不包括圆上的点)问题5 知识运用:有两个同心圆,大圆半径
为 ,小圆半径为 ,求圆环的面积。 因为圆环的面积是大圆面积与小圆面积的差,
所以,圆环的面积为
范例探究例题 用一根长1米、一根长2米的绳子围成两个同心圆,这两个圆半径之差是多少?(保留3位小数)长1米的绳子围成的圆的半径为 米,
长2米的绳子围成的圆的半径为 米,
所以,两个同心圆半径之差为
挖掘内涵出真知创新与拓展 把地球的赤道近似地看做一个圆,如果环绕地球赤道有一个圆,它的周长比赤道的周长多一米,这两个同心圆半径之差是多少?设地球的半径为r,因为赤道与环绕赤道的圆是两个同心圆,所以这两个圆半径之差为挖掘内涵出真知思考? 是不是只要告诉我们两个同心圆的周长之差是1米,它们的半径之差就是一个固定值呢?答案:那是肯定的!!!!课堂练习1.判断题
(1)长度相等的两条弧是等弧;( )
(2)等圆的半径相等,圆心的位置必须相同。( )
2.如图,ABCD是正方形,边长为,以B为圆心,
以BA为半径画弧,则阴影面积为 。
3.有两个同心圆,如果小圆的半径等于大圆
半径的 ,求圆环部分的面积与小圆面积的比。××
1.以已知点O为圆心,已知线段为半径作圆,可以( )
A.1个 B.2个 C.3个 D.无数个
(思考:这个题目考查了我们哪个知识点?)
2.如图,已知⊙O1、⊙O2中弧AB与弧CD相等,并且
O1E=2,∠HO2G=90°,试求线段GH的值.
(思考:这个题目考查了我们哪个知识点?)达标测试A活动与探究 如图,AB为半圆 O的直径,以AO为直径作半圆O1,再以
为直径作半圆O2,再以 为直径作半圆 O3和 O4 ,一只
蚂蚁要从A 点沿图弧爬到B点,它选择走大半圆近,还是走4个
小半圆组成的路径近?谢谢!
2.用集合的观点来描述圆的概念
3.在平面内,一个点与一个圆有怎样的位置关
系?(用画图的方法展示一下)
4.如图,指出图中所示的量:
圆心 ;半径 ;
直径 ;优弧 ;
劣弧 ;扇形 .学 习 目 标1.理解等圆、同心圆、等弧、圆环等概念;
2.会用圆的面积与周长公式进行有关简单
问题的计算;
3.会利用圆的有关知识解决与圆有关的问题.实验与探究 分别观察图(1)与图(2),你发现图(1)中的两枚硬币所确定的两个圆有什么特点(也可以自己取两枚相同硬币来观察)?图(2)中的几个圆有什么共同点和不同点?能够重合的圆叫做等圆圆心相同、半径不等的圆叫做同心圆交流与发现问题1 各小组由一名同学说出一个数字,然后每个人都以这个数字为半径做一个圆,然后同学之间相互将所画的圆重叠,看看有什么发现?然后和其他小组交流
你们小组的发现是:
其他小组和你们小组的发现相同吗?只要是半径确定了,所画的圆均能够重合 虽然每个小组在画圆时半径不相同,但各自所画的圆
都能够重合相同问题2 判断:能够重合的两段弧就是等弧对吗?
那必须具备怎样的条件的弧才是等弧呢?
试一试找出下图中的等弧 在等圆或同圆中,能够互
相重合的弧叫做 等弧问题3 你能用圆规作出几个圆心相同但半径不同
的圆吗?试试看!
(这样的圆课本上给它们取了怎么有趣的名字?) 同心圆问题4 讨论:由问题3,我们知道由两个圆心相同但半径不同的两个圆就组成同心圆,我们把两个同心圆之间的部分叫做圆环,那么你能用图形表示“到点A的距离大于2厘米而小于3厘米的点的集合”吗?解:如图,为两圆之间的圆环部分(不包括圆上的点)问题5 知识运用:有两个同心圆,大圆半径
为 ,小圆半径为 ,求圆环的面积。 因为圆环的面积是大圆面积与小圆面积的差,
所以,圆环的面积为
范例探究例题 用一根长1米、一根长2米的绳子围成两个同心圆,这两个圆半径之差是多少?(保留3位小数)长1米的绳子围成的圆的半径为 米,
长2米的绳子围成的圆的半径为 米,
所以,两个同心圆半径之差为
挖掘内涵出真知创新与拓展 把地球的赤道近似地看做一个圆,如果环绕地球赤道有一个圆,它的周长比赤道的周长多一米,这两个同心圆半径之差是多少?设地球的半径为r,因为赤道与环绕赤道的圆是两个同心圆,所以这两个圆半径之差为挖掘内涵出真知思考? 是不是只要告诉我们两个同心圆的周长之差是1米,它们的半径之差就是一个固定值呢?答案:那是肯定的!!!!课堂练习1.判断题
(1)长度相等的两条弧是等弧;( )
(2)等圆的半径相等,圆心的位置必须相同。( )
2.如图,ABCD是正方形,边长为,以B为圆心,
以BA为半径画弧,则阴影面积为 。
3.有两个同心圆,如果小圆的半径等于大圆
半径的 ,求圆环部分的面积与小圆面积的比。××
1.以已知点O为圆心,已知线段为半径作圆,可以( )
A.1个 B.2个 C.3个 D.无数个
(思考:这个题目考查了我们哪个知识点?)
2.如图,已知⊙O1、⊙O2中弧AB与弧CD相等,并且
O1E=2,∠HO2G=90°,试求线段GH的值.
(思考:这个题目考查了我们哪个知识点?)达标测试A活动与探究 如图,AB为半圆 O的直径,以AO为直径作半圆O1,再以
为直径作半圆O2,再以 为直径作半圆 O3和 O4 ,一只
蚂蚁要从A 点沿图弧爬到B点,它选择走大半圆近,还是走4个
小半圆组成的路径近?谢谢!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
