青岛版数学八年级下册第6章 平行四边形单元测试卷(含答案)
文档属性
| 名称 | 青岛版数学八年级下册第6章 平行四边形单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 80.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览


文档简介
青岛版数学八年级下册第六单元测试卷
一、选择题
1.下列命题中,正确的是?( ???)
A.?对角线互相垂直且相等的四边形是菱形???????????????B.?对角线互相垂直的平行四边形是菱形 C.?对角线互相平分且相等的四边形是菱形???????????????D.?对角线相等的四边形是菱形
2.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是(?? )
A.?∠ABC=90°???????????????????????????????B.?AC=BD???????????????????????????????C.?OA=OB???????????????????????????????D.?OA=AB
3.已知下列命题中:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形;其中正确的有( ).
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
4.用两个边长为a的等边三角形纸片拼成的四边形是( ).
A.?等腰梯形?????????????????????????????????B.?正方形?????????????????????????????????C.?矩形?????????????????????????????????D.?菱形
5.在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是(?? )
A.?四边形AEDF是平行四边形??????????????????????????????????B.?如果∠BAC=90°,那么四边形AEDF是矩形 C.?如果AD⊥BC,那么四边形AEDF是菱形??????????????D.?如果AD平分∠BAC,那么四边形AEDF是菱形
6.如图,在□ABCD中,如果EF∥AD , GH∥CD , EF与GH相交与点O , 那么图中的平行四边形一共有(??? ).
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?8个???????????????????????????????????????D.?9个
7.已知?ABCD的周长为32,AB=4,则BC等于(?? )
A.?4?????????????????????????????????????????B.?12?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
8.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.?选①②???????????????????????????????B.?选①③??????????????????????????C.?选②④??????????????????????????????D.?选②③
9.下列条件中,不能判定四边形是平行四边形的是(? )
A.?两组对边分别平行??????????????????????????????????????????????B.?一组对边平行,另一组对边相等 C.?两组对边分别相等??????????????????????????????????????????????D.?一组对边平行且相等
10.如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( ) ①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°. ?
A.?①????????????????????????????????B.?①②?????????????????????????????????C.?①②③??????????????????????????????????D.?都不正确
11.如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2, 则DC和EF的大小关系是( )
A.?DC>EF?????????????????????????????B.?DC<EF?????????????????????????????C.?DC=EF?????????????????????????????D.?无法比较
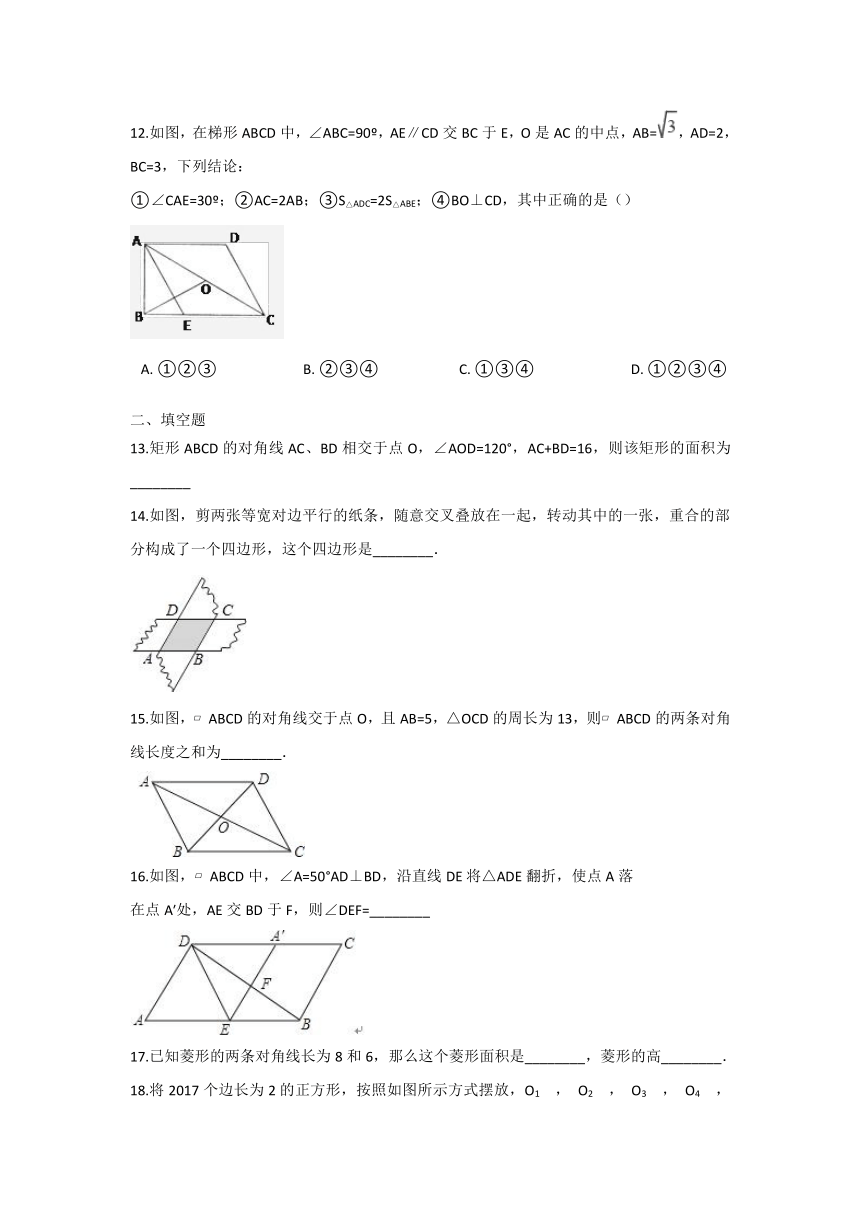
12.如图,在梯形ABCD中,∠ABC=90o,AE∥CD交BC于E,O是AC的中点,AB=,AD=2,BC=3,下列结论: ①∠CAE=30o;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是() ?
A.?①②③?????????????????????????B.?②③④???????????????????????C.?①③④????????????????????????????D.?①②③④
二、填空题
13.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC+BD=16,则该矩形的面积为________
14.如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
15.如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则?ABCD的两条对角线长度之和为________.
16.如图,?ABCD中,∠A=50°AD⊥BD,沿直线DE将△ADE翻折,使点A落 在点A′处,AE交BD于F,则∠DEF=________?
17.已知菱形的两条对角线长为8和6,那么这个菱形面积是________,菱形的高________.
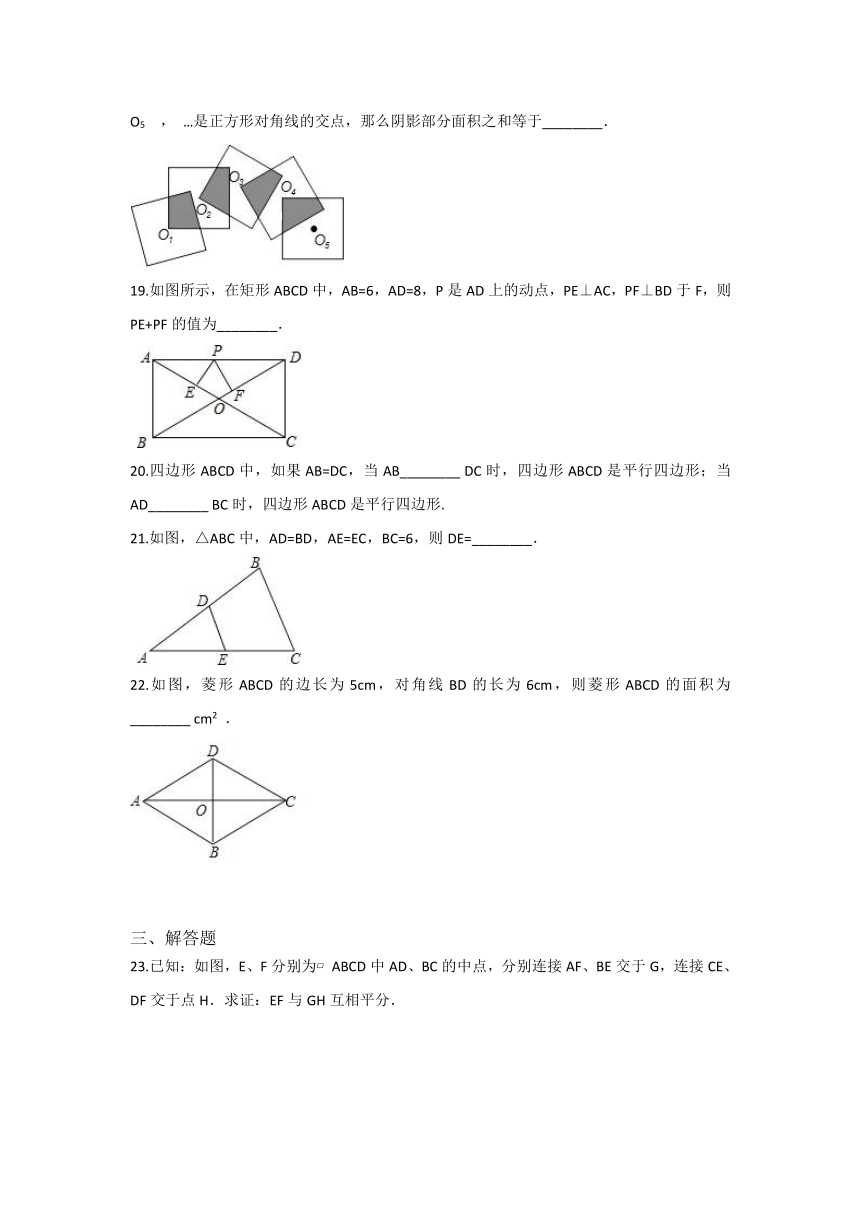
18.将2017个边长为2的正方形,按照如图所示方式摆放,O1 , O2 , O3 , O4 , O5 , …是正方形对角线的交点,那么阴影部分面积之和等于________.
19.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为________.
20.四边形ABCD中,如果AB=DC,当AB________?DC时,四边形ABCD是平行四边形;当AD________?BC时,四边形ABCD是平行四边形.
21.如图,△ABC中,AD=BD,AE=EC,BC=6,则DE=________.
22.如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为________?cm2 .
三、解答题
23.已知:如图,E、F分别为?ABCD中AD、BC的中点,分别连接AF、BE交于G,连接CE、DF交于点H.求证:EF与GH互相平分.
24.如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点. (Ⅰ)求证:MD和NE互相平分; (Ⅱ)若BD⊥AC,EM=2 ,OD+CD=7,求△OCB的面积.
25.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E. (1)求证:EO=FO; (2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论; (3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论 。
26.如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
答案解析
一、选择题
B D C D C D B D B C C D
二、填空题
13. 16
14. 菱形
15. 16
16. 65°
17. 24;
18. 2016
19.
20. 平行;=
21. 3
22. 24
三、解答题
23. 证明:∵E为AD的中点,F为BC的中点, ∴AE= AD,CF= BC, ∵四边形ABCD是平行四边形, ∴AD∥BC,∴AE∥CF,AE=CF, ∴四边形AFCE是平行四边形, ∴AF∥CE, 同理可证:BE∥DF, ∴四边形GFHE是平行四边形, ∴EF与GH互相平分
24. (Ⅰ)证明:连接ED、MN,∵CE、BD是△ABC的中线, ∴E、D是AB、AC中点, ∴ED∥BC,ED= BC, ∵M、N分别为OB、OC的中点, ∴MN∥BC,MN= BC, ∴ED∥MN,ED=MN, ∴四边形DEMN是平行四边形, ∴MD和NE互相平分; (Ⅱ)解:由(Ⅰ)可得DN=EM=2 , ∵BD⊥AC, ∴∠ODC=90°, ∵N是OC的中点, ∴OC=2DN=4 (直角三角形斜边中线等于斜边的一半) ∵OD2+CD2=OC2=32, (OD+CD)2=OD2+CD2+2OD×CD=72=49, 2OD×CD=49﹣32=17, OD×CD=8.5, ∵OB=2OM=2OD, ∴S△OCB= OB×CD=OD×CD=8.5.
25. 解:(1)∵CE平分∠ACB, ∴∠ACE=∠BCE, ∵MN∥BC, ∴∠OEC=∠ECB, ∴∠OEC=∠OCE, ∴OE=OC, 同理,OC=OF, ∴OE=OF; (2)当点O运动到AC中点处时,四边形AECF是矩形. 如图AO=CO,EO=FO, ∴四边形AECF为平行四边形, ∵CE平分∠ACB, ∴∠ACE=∠ACB, 同理,∠ACF=∠ACG, ∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°, ∴四边形AECF是矩形; (3)△ABC是直角三角形 ∵四边形AECF是正方形, ∴AC⊥EN,故∠AOM=90°, ∵MN∥BC, ∴∠BCA=∠AOM, ∴∠BCA=90°, ∴△ABC是直角三角形.
26. (1)解:当四边形ABQP是矩形时,BQ=AP,即:t=8﹣t, 解得t=4. 答:当t=4时,四边形ABQP是矩形 (2)解:设t秒后,四边形AQCP是菱形 当AQ=CQ,即 =8﹣t时,四边形AQCP为菱形. 解得:t=3. 答:当t=3时,四边形AQCP是菱形 (3)解:当t=3时,CQ=5,则周长为:4CQ=20cm, 面积为:4×8﹣2× ×3×4=20(cm2)
一、选择题
1.下列命题中,正确的是?( ???)
A.?对角线互相垂直且相等的四边形是菱形???????????????B.?对角线互相垂直的平行四边形是菱形 C.?对角线互相平分且相等的四边形是菱形???????????????D.?对角线相等的四边形是菱形
2.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是(?? )
A.?∠ABC=90°???????????????????????????????B.?AC=BD???????????????????????????????C.?OA=OB???????????????????????????????D.?OA=AB
3.已知下列命题中:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形;其中正确的有( ).
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
4.用两个边长为a的等边三角形纸片拼成的四边形是( ).
A.?等腰梯形?????????????????????????????????B.?正方形?????????????????????????????????C.?矩形?????????????????????????????????D.?菱形
5.在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是(?? )
A.?四边形AEDF是平行四边形??????????????????????????????????B.?如果∠BAC=90°,那么四边形AEDF是矩形 C.?如果AD⊥BC,那么四边形AEDF是菱形??????????????D.?如果AD平分∠BAC,那么四边形AEDF是菱形
6.如图,在□ABCD中,如果EF∥AD , GH∥CD , EF与GH相交与点O , 那么图中的平行四边形一共有(??? ).
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?8个???????????????????????????????????????D.?9个
7.已知?ABCD的周长为32,AB=4,则BC等于(?? )
A.?4?????????????????????????????????????????B.?12?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
8.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.?选①②???????????????????????????????B.?选①③??????????????????????????C.?选②④??????????????????????????????D.?选②③
9.下列条件中,不能判定四边形是平行四边形的是(? )
A.?两组对边分别平行??????????????????????????????????????????????B.?一组对边平行,另一组对边相等 C.?两组对边分别相等??????????????????????????????????????????????D.?一组对边平行且相等
10.如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( ) ①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°. ?
A.?①????????????????????????????????B.?①②?????????????????????????????????C.?①②③??????????????????????????????????D.?都不正确
11.如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2, 则DC和EF的大小关系是( )
A.?DC>EF?????????????????????????????B.?DC<EF?????????????????????????????C.?DC=EF?????????????????????????????D.?无法比较
12.如图,在梯形ABCD中,∠ABC=90o,AE∥CD交BC于E,O是AC的中点,AB=,AD=2,BC=3,下列结论: ①∠CAE=30o;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是() ?
A.?①②③?????????????????????????B.?②③④???????????????????????C.?①③④????????????????????????????D.?①②③④
二、填空题
13.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC+BD=16,则该矩形的面积为________
14.如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
15.如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则?ABCD的两条对角线长度之和为________.
16.如图,?ABCD中,∠A=50°AD⊥BD,沿直线DE将△ADE翻折,使点A落 在点A′处,AE交BD于F,则∠DEF=________?
17.已知菱形的两条对角线长为8和6,那么这个菱形面积是________,菱形的高________.
18.将2017个边长为2的正方形,按照如图所示方式摆放,O1 , O2 , O3 , O4 , O5 , …是正方形对角线的交点,那么阴影部分面积之和等于________.
19.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为________.
20.四边形ABCD中,如果AB=DC,当AB________?DC时,四边形ABCD是平行四边形;当AD________?BC时,四边形ABCD是平行四边形.
21.如图,△ABC中,AD=BD,AE=EC,BC=6,则DE=________.
22.如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为________?cm2 .
三、解答题
23.已知:如图,E、F分别为?ABCD中AD、BC的中点,分别连接AF、BE交于G,连接CE、DF交于点H.求证:EF与GH互相平分.
24.如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点. (Ⅰ)求证:MD和NE互相平分; (Ⅱ)若BD⊥AC,EM=2 ,OD+CD=7,求△OCB的面积.
25.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E. (1)求证:EO=FO; (2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论; (3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论 。
26.如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
答案解析
一、选择题
B D C D C D B D B C C D
二、填空题
13. 16
14. 菱形
15. 16
16. 65°
17. 24;
18. 2016
19.
20. 平行;=
21. 3
22. 24
三、解答题
23. 证明:∵E为AD的中点,F为BC的中点, ∴AE= AD,CF= BC, ∵四边形ABCD是平行四边形, ∴AD∥BC,∴AE∥CF,AE=CF, ∴四边形AFCE是平行四边形, ∴AF∥CE, 同理可证:BE∥DF, ∴四边形GFHE是平行四边形, ∴EF与GH互相平分
24. (Ⅰ)证明:连接ED、MN,∵CE、BD是△ABC的中线, ∴E、D是AB、AC中点, ∴ED∥BC,ED= BC, ∵M、N分别为OB、OC的中点, ∴MN∥BC,MN= BC, ∴ED∥MN,ED=MN, ∴四边形DEMN是平行四边形, ∴MD和NE互相平分; (Ⅱ)解:由(Ⅰ)可得DN=EM=2 , ∵BD⊥AC, ∴∠ODC=90°, ∵N是OC的中点, ∴OC=2DN=4 (直角三角形斜边中线等于斜边的一半) ∵OD2+CD2=OC2=32, (OD+CD)2=OD2+CD2+2OD×CD=72=49, 2OD×CD=49﹣32=17, OD×CD=8.5, ∵OB=2OM=2OD, ∴S△OCB= OB×CD=OD×CD=8.5.
25. 解:(1)∵CE平分∠ACB, ∴∠ACE=∠BCE, ∵MN∥BC, ∴∠OEC=∠ECB, ∴∠OEC=∠OCE, ∴OE=OC, 同理,OC=OF, ∴OE=OF; (2)当点O运动到AC中点处时,四边形AECF是矩形. 如图AO=CO,EO=FO, ∴四边形AECF为平行四边形, ∵CE平分∠ACB, ∴∠ACE=∠ACB, 同理,∠ACF=∠ACG, ∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°, ∴四边形AECF是矩形; (3)△ABC是直角三角形 ∵四边形AECF是正方形, ∴AC⊥EN,故∠AOM=90°, ∵MN∥BC, ∴∠BCA=∠AOM, ∴∠BCA=90°, ∴△ABC是直角三角形.
26. (1)解:当四边形ABQP是矩形时,BQ=AP,即:t=8﹣t, 解得t=4. 答:当t=4时,四边形ABQP是矩形 (2)解:设t秒后,四边形AQCP是菱形 当AQ=CQ,即 =8﹣t时,四边形AQCP为菱形. 解得:t=3. 答:当t=3时,四边形AQCP是菱形 (3)解:当t=3时,CQ=5,则周长为:4CQ=20cm, 面积为:4×8﹣2× ×3×4=20(cm2)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
