人教A版数学必修四第一章 三角函数 基础性测试卷word版含答案
文档属性
| 名称 | 人教A版数学必修四第一章 三角函数 基础性测试卷word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 263.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 22:59:09 | ||
图片预览



文档简介
第一章 三角函数 基础性测试卷
班级 姓名 学号 成绩
一、选择题(每小题3分,共36分)
1.在△ABC中,∠C=90°,a、b分别是∠A、∠B所对的两条直角边,c是斜边,则有( )是正确的。
A、sinA= B、cosB= C、sinB= D、tanA=
2.如图,在中,=3,=4,=5,则的值是( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,cosA=,则BC∶AC∶AB等于( )
A、1∶2∶5 B、1∶∶ C、1∶∶2 D、1∶2∶
4.在中,,, 则等于( )
A. B. C. D.
5.如图,已知正方形的边长为2,如果将线段绕着点旋转后,点落在的延长线上的点处,那么等于( )
A.1 B. C. D.
6.在△ABC中,若tanA=1,sinB=,你认为最确切的判断是( )
A.△ABC是等腰三角形 B.△ABC是等腰直角三角形
C.△ABC是直角三角形 D.△ABC是一般锐角三角形
7.某市为了美化环境,计划在如图所示的三角形空地上种植
草皮,已知这种草皮每平方米售价为元,则购买这
种草皮至少需要 ( )
A.450元 B.225元 C.150元 D.300元
8.身高相同的甲、乙、丙三人放风筝,各人放出线长分别为300米、350米、280米,线与地面的夹角分别为30°、45°、60°(假设风筝线是拉直的),三人所放风筝( )
A.甲的最高 B.乙的最高 C.丙的最高 D.一样高
9.如图,在某海岛的观察所A测得船只B的俯角是30°.若观察所的标高(当水位为0m时的高度)是53m,当时的水位是+3m,则观察所A和船只B的水平距离BC是( )
A.50 m B. m C.53 m D.m
10.已知在Rt△ABC中,∠C=90°.若sinA=,则sinB等于( )
A、? B、 C、 D、1
11.等腰三角形的一腰长为6cm,底边长为6cm,则其底角为( )。
A. 120° B. 90° C. 60° D. 30°
12.如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN
交AC于D,连结BD,若cos∠BDC=,则BC的长是( )
A、4cm B、6cm C、8cm D、10cm
二、填空题(每小题3分,共12分)
13.在△ABC中.∠C=90°,若tanA=1,则∠B= 度
14. 已知在△ABC中,∠C=90°,3cosB=2,AC=,则AB= .
15.在中,,,,则 度
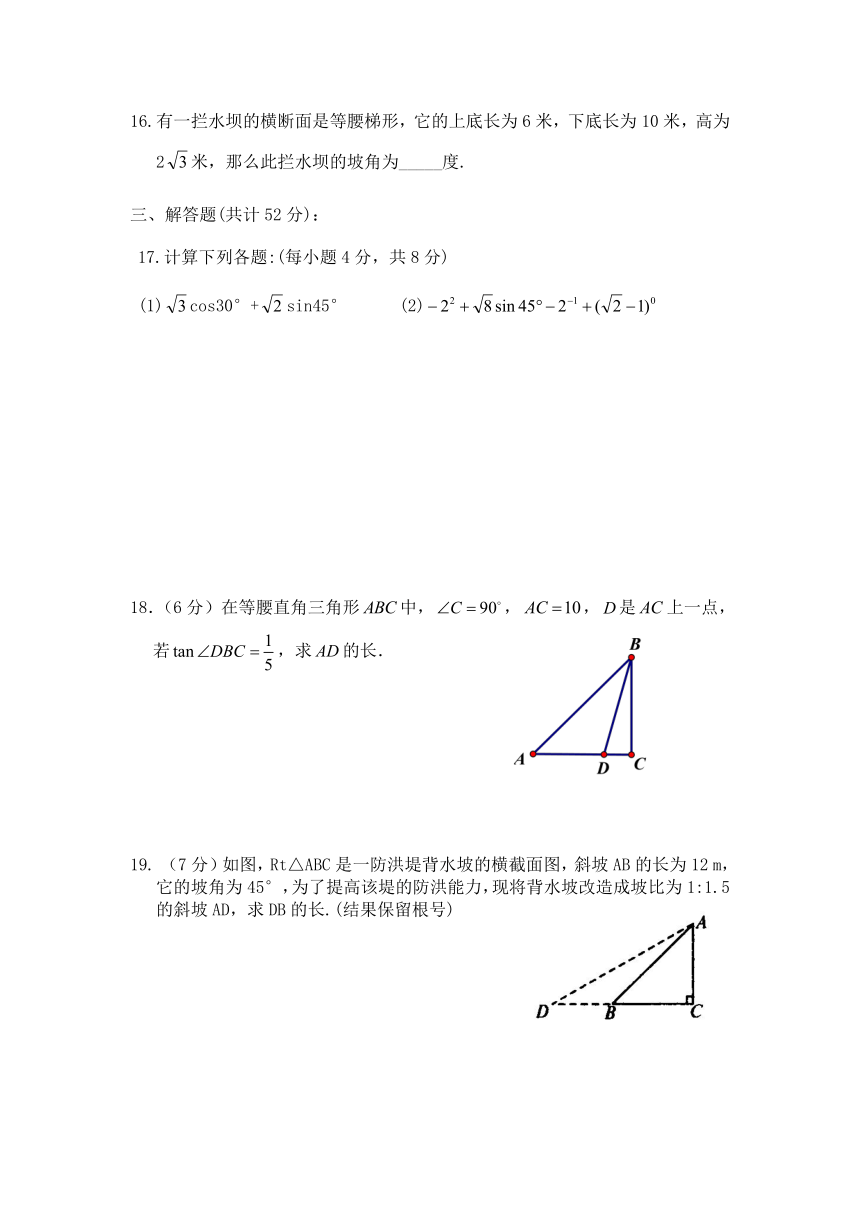
16.有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2米,那么此拦水坝的坡角为_____度.
三、解答题(共计52分):
17.计算下列各题:(每小题4分,共8分)
(1)cos30°+sin45° (2)
18.(6分)在等腰直角三角形中,,,是上一点,若,求的长.
19. (7分)如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12 m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,求DB的长.(结果保留根号)
20. (7分)在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求:CD和sinC
21. (7分)如图,小亮在操场上距离旗杆AB的C处,用测角仪测得旗杆顶端A的仰角为30°,已知BC=9m,测角仪高CD为1m,求旗杆AB的高(结果保留根号)。
22.(8分)一艘轮船自西向东航行,在A处测得北偏东60°方向有一座小岛F,继续向东航行80海里到达C处,测得小岛F此时在轮船的北偏西30°方向上.轮船在整个航行过程中,距离小岛F最近是多少海里?(结果保留根号)
23. (9分)如图,某货船以20海里/小时的速度将一批重要的物资由A处运往正西方向的B处,经16小时的航行到达,到达后便接到气象部门通知,一台风中心正由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.
问B处是否会受到影响?请说明理由。
参考答案
1、 选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D A C B B B C B B B D A
2、 填空题:
题号 13 14 15 16
答案 45 6 30 60
三、解答题:
17.(1)解:原式= (2)解:原式=
= =
= =
18. 解:在Rt△ABC中
∵AB=AC=10
∴ DC=2
∴ AD=8
19.解:在Rt△ABC中
在Rt△ADC中, AC:DC=1:1.5
DC=
∴ DB=DC-BC=(米)
答: DB的长为米
20.解:在Rt△ABD中,由勾股定理,得:
BD=
∴ CD=BC-BD=10
在Rt△ADC中,
AC=
∴ sinC=
21.解:过D作DE⊥AB,垂足为E
在Rt△ADE中,∠ADE=30°,DE=9
∴ AB=AE+EB=(米)
答:旗杆AB的高为()米
22.解:过点F作DF⊥AC,垂足为D
在Rt△ADF中,∠FAD=30°
在Rt△CDF中,∠FCD=60°
∵ AC=AD+CD=80
∴ ,解,得:(海里)
答:距离小岛F最近距离为海里
23.解:过B作BD⊥AC,垂足为D
在Rt△ABD中,∠BAD=30°
AB=20×16=320海里
由
得:BD=
∴ 在B处的货船会受到台风的侵袭
2题图
5题图
7题图
A
